Digitalfilter mit ATmega
Auch mit 8-Bit-Mikrocontrollern der ATmega-Reihe ist es möglich, einfache digitale Signalverarbeitungen auszuführen. Mittels kostenloser Mathematiksoftware ist die Berechnung eigener Filter möglich.
Viele von uns haben schon analoge Filterschaltungen aufgebaut, als passive LC-Filter oder aktive Filter mit Operationsverstärkern. Dank kostenloser Berechnungssoftware, wie z. B. AADE, ist die Auswahl der Schaltung und Berechnung der Bauteilwerte kein Problem mehr. Die gleichen Filter in digitaler Technik zu erstellen gilt dagegen immer noch als kompliziert, obwohl sie in professionellen Schaltungen die Analogtechnik weitgehend verdrängt haben. Ihr großer Vorteil ist der fehlende Abgleich. Dank Quarzoszillator wird ein einmal berechneter Frequenzgang ohne Präzisionsbauteile reproduzierbar eingehalten.
Die Software ist im Grunde sehr einfach aufgebaut, besteht nur aus Schiebeoperationen, Additionen und einigen Multiplikationen. Die ATmega-Controller enthalten alle dazu nötigen Funktionen, einen A/D-Wandler, einen 8-Bit Multiplizierer und mehrere D/A-Wandler durch Pulsbreitenmodulation. Am Ausgang muß nur noch ein einfacher Tiefpaß die PWM-Frequenz wegfiltern. Die Programmbeispiele wurden auf Grundlage der Applikationsschrift AVR223 mit AVRStudio entwickelt.
Am Ende der Programme befindet sich eine Koeffiziententabelle, deren Werte die Filtereigenschaften bestimmen. Um eigene Filter entwickeln zu können sollen dazu die Grundbegriffe sehr kurz erläutert und dann einfache „Kochrezepte“ vorgestellt werden.
Ein IIR-Filter 6. Ordnung
Als erstes wird ein Filter berechnet, das nur durch Änderung der Koeffizienten als Tiefpaß, Hochpaß, Bandpaß oder Bandsperre wirkt. Im Beispielprogramm soll es ein 1750 Hz Sperrfilter werden, das laute Ruftöne beim Zuhören auf Amateur-Relaisfunkstellen unterdrücken kann. Dieser Filtertyp heißt „IIR“, infinite impulse response, weil er nach Anregung mit einem Impuls theoretisch eine unendliche Impulsantwort liefert. Der verwendete Aufbau aus drei hintereinandergeschalteten Teilfiltern zweiter Ordnung ist als gutmütig bekannt. Diese kaskadierten Teilfilter nennt man „SOS“ second order sections oder auch biquad sections. Der Aufbau mit einem einzigen Filter 6. Ordnung, wie er in der AVR223 von 2001 noch beschrieben ist, neigt auf Grund der endlichen Genauigkeit der Koeffizienten eher zum Schwingen.
Software zur Koeffizientenberechnung
Es gibt einige spezialisierte Programme, die aber nur eine kleine Anzahl von Digitalfilterkonfigurationen kennen, z. B. FilterFree. Wesentlich universeller sind umfangreiche Programmpakete für numerische Mathematik. Neben dem kommerziellen Matlab das auch in einer eingeschränkten Studentenversion angeboten wird, und zu dem zahlreiche Literatur existiert, z. B. ISBN 9783486584271 , gibt es auch zwei kostenlose Nachahmer: Octave und Scilab. Spezialitäten der digitalen Signalverarbeitung bilden nur einen kleinen Teil des Gesamtpakets, und die Hilfetexte dazu sind sehr knapp oder auch mal ein Jahrzehnt alt. Zum Glück sind beide Programme dem Vorbild so nahe, daß man vieles der Literatur zu Matlab entnehmen kann. Die eigentliche Koeffizientenberechnung besteht meistens aus nur wenigen Textzeilen. Man gibt wie beim analogen Filter die gewünschten Durchlaß- und Sperrfrequenzen, die Filtercharakteristik und Ordnung ein. Auf eine grafische Benutzeroberfläche muß man allerdings verzichten. Immerhin können der Frequenzgang und andere Kurven grafisch ausgegeben werden.
Transformationen und komplexe Zahlen
Die mathematischen Grundbegriffe der Digitalfilterberechnung sollen hier nur stichwortartig erwähnt werden:
Von der Fourier-Transformation hat man schon mal gehört, ihre Bedeutung ist noch einigermaßen begreifbar. Von einem periodischen Signal x(t) wie es das Oszilloskop zeigt, also im Zeitbereich, gelangt man über sie zur spektralen Darstellung x(f) im Frequenzbereich auf dem Spektrumanalysator. Das ist aber nur die halbe Information, eigentlich gehört zu jeder Harmonischen außer der angezeigten Amplitude auch noch ihre Phasenlage. x(f) ist also eine zweidimensionale Variable, Amplitude (Betrag) und Phase (Winkel) sind polare Koordinaten. Wenn wir zu kartesischen Koordinaten übergehen, und die x- Achse als reelle, die y-Achse als imaginäre Achse bezeichnen, kommen wir zur komplexen Zahlendarstellung. Für die Berechnung analoger Filter ist die Laplace-Transformation zuständig, für digitale Filter die nahe verwandte z-Transformation. Im ersten Fall wird x(t) in ein X(s) transformiert, in unserem Fall, wie der Name schon sagt in ein X(z). Zur besseren Unterscheidung wird das X groß geschrieben. Auch hier rechnen wir mit komplexen Zahlen, wir befinden uns nach der Transformation in der komplexen z-Ebene.
Übertragungsfunktion und Koeffizienten
Das Digitalfilter ist für uns zunächst ein schwarzer Kasten, in den ein Signal x(t) hineinläuft und als gefiltertes Signal y(t) wieder herauskommt. Die z-transformierten Signale heißen X(z) und Y(z). Der Quotient Y(z)/X(z) = H(z) wird Übertragungsfunktion, engl. transfer function genannt. Für bestimmte Werte von z wird der Zähler oder Nenner der Übertragungsfunktion Null, diese heißen Nullstellen und Pole der Funktion. Diese Werte der komplexen Zahl z können im Pol/Nullstellendiagramm als Punkte in der z-Ebene dargestellt werden, das hilft beispielsweise bei der Untersuchung der Stabilität des Filters gegen Schwingneigung.
Die genannten Mathematikprogramme berechnen uns aus den gewünschten Filterdaten die Übertragungsfunktion. Im einfachsten Fall können wir daraus die Zahlenwerte direkt in die Filtersoftware als Koeffiziententabelle eintragen. Die Aufteilung in Teilfilter macht die Berechnung etwas umständlicher. Die einzelnen Übertragungsfunktionen werden multipliziert, also Y(z)/X(z) = H1(z)*H2(z)*H3(z). Wir müssen also H(z) in geeignete Faktoren zerlegen, auch dabei hilft uns die Mathematiksoftware.
Octave und Scilab
Am besten installieren wir gleich beide Softwarepakete. Beide bieten unterschiedliche Lösungswege zur Berechnung der gewünschten SOS-Teilfilter. In Scilab werden Frequenzen als Bruchteile der Abtastfrequenz, engl. sample rate des Analog-Digitalwandlers angegeben. Der AD-Wandler im ATmega wird hier mit einer Taktfrequenz von 1/64 des Quarzoszillators betrieben und braucht pro Wandlung 13 Takte. Mit einem 15 MHz – Quarz ergibt sich also ein Abtastfrequenz von 15MHz/(64*13) = 18029 Hz. Octave rechnet mit Bruchteilen der halben Abtastfrequenz, auch Nyquist-Frequenz genannt. Die Filterordnung bezieht sich in beiden Programmen auf Tief- und Hochpassfilter. Für Bandpässe und -sperren muß die Hälfte angegeben werden, hier also 3 statt 6.
Beginnen wir mit Scilab. Das kurze Programm in Bild 1 speichern wir als Textdatei z. B. unter „Sperrfilter1750Hz.sci“ ab, dann lädt es durch Anklicken direkt in den bunten Scilab-Editor und wird mit „Ausführen – in Scilab laden“ gestartet. Ein neues Fenster mit der Frequenzgangkurve öffnet sich und im Scilab-Hauptfenster stehen die Übertragungsfunktionen der drei Teilfilter, sowie die Gesamtverstärkung gain. Die Filterordnung kann nicht direkt vorgegeben werden, wir müssen die vier Grenzfrequenzen und die beiden Dämpfungswerte variieren bis genau drei SOS-Teilfilter herauskommen. In Octave werden nur zwei Grenzfrequenzen verlangt, dafür können wir die Filterordnung vorgeben. Wieder wird eine Textdatei ausgeführt und liefert Übertragungsfunktionen für drei Teilfilter.
Einen Schönheitsfehler haben die berechneten Funktionen noch. In der Regelungstechnik und auch in Scilab/Octave wird mit positiven Exponenten von z gerechnet, die Literatur zur digitalen Signalverarbeitung benutzt dagegen negative. Wenn wir aber Zähler und Nenner jeder Teil-Übertragungsfunktion durch z2 teilen, ändert sie sich nicht und wir haben die Formel wie sie für digitale Filter üblich ist.
Jetzt können wir die Koeffizienten direkt aus den Übertragungsfunktionen ablesen. Wir müssen sie noch skalieren, also mit einer geeigneten Zweierpotenz multiplizieren und zu einer ganzen Zahl auf/abrunden. Sie sollen hier zu einer 16 Bit-Zahl (Festkommadarstellung mit Vorzeichenbit) werden, also alle Koeffizienten im Bereich -32768...+32767 liegen.
Frequenzgang maßgeschneidert
Mit der Funktion yulewalk können wir auch kompliziertere Frequenzgangkurven erreichen. In Octave fehlt sie, drei ähnlich lautende Funktionen haben nichts mit Filtern zu tun. Die gewünschte Funktion wird mit Geradenstücken zwischen beliebigen Kurvenpunkten vorgegeben. Als Beispiel nehmen wir einen Bandpass für SSTV slow scan television, der 1974 in der "CQ-DL" vorgestellt wurde. Synchronimpuls (1200 Hz) und Bildinformation (1500-2300 Hz) sollen durchgelassen, Störungen außerhalb dieser Bereiche unterdrückt werden. Nach längerem Ausprobieren verschiedener Vorgabewerte und Reduktion der Abtastfrequenz auf die Hälfte ergibt sich eine gute Übereinstimmung mit dem Frequenzgang des Originals. Jetzt haben wir eine Übertragungsfunktion 6.Ordnung, die wieder in SOS-Teilfilter zerlegt werden muß. Diese Funktion tf2sos transfer function to second order sections fehlt in Scilab, deshalb übertragen wir die Zahlen aus Scilab nach Octave und erhalten so schließlich unsere Koeffizienten.
Es gibt noch weitere Verfahren, um "Wunschfrequenzgänge" zu berechnen:
prony in Matlab ( in Scilab nicht vorhanden) hier im Forum erwähnt - in ISBN 9780792395591 ab Seite 35 steht ein Matlab-m-file dazu,
Update: es gibt inzwischen (seit2013) eine Signal processing toolbox für Scilab, die auch "prony" (und ähnlich auch "stmcb") enthält.
und
FDLS (frequency domain least square) von Greg Berchin:
Matlab-File und PDFs dazu,
Diskussion auf fpgacentral.com Grundlagenartikel "Precise Filter Design" Auch als Kapitel 7 in ISBN 9781118316917 oder ? ISBN 9781118278383 (2.Auflage 2012) oder ISBN 9780470131572 (2007) ab Seite 59 zu finden
Von der Übertragungsfunktion zum Programm
Unsere SOS-Teilfilter haben jetzt (je nach Vorzeichen der Exponenten) diese Übertragungsfunktion:
- [math]\displaystyle{ H(z)=\frac{b_{2}\cdot z^{-2}+b_{1}\cdot z^{-1}+b_{0}}{a_{2}\cdot z^{-2}+a_{1}*z^{-1}+1} = {\frac{b_{2}+b_{1}\cdot z+b_{0}\cdot z^{2}}{a_{2}+a_{1}\cdot z+z^{2}}} }[/math]
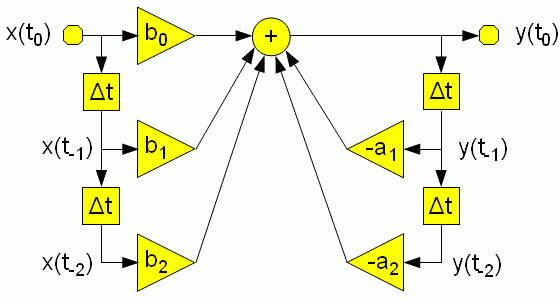
Jetzt wird von z-Bereich wieder in den Zeitbereich rücktransformiert. Diese Funktion y(t)= f(x(t))und der dazugehörige Programmablauf wird üblicherweise in Form eines Blockdiagramms dargestellt:
Wir sehen drei Blocktypen: ein Verzögerung um einen Sampletakt Δt, Addition mehrere Summanden, und Multiplikationen mit Konstanten, die aus der Übertragungsfunktion abgelesen werden. Spezielle Signalprozessoren enthalten übrigens für die beiden letzteren einen sogenannten MAC multiply-accumulate Befehl. Im Atmega-Programm wird es in einem Assembler-Macro namens SMAC32 durchgeführt.
Literatur
- Der wichtigste Artikel zur Signalverarbeitung mit Scilab ist Signal.pdf (1,2MByte) von 1998. Die dazugehörigen Programme sind etwas schwerer zu finden, hier habe ich sie daher zu SignalFiles.pdf (980kB) zusammengefasst.
- Bücher zu Scilab gibt es nur wenige, und diese gehen nicht auf das Thema Signalverarbeitung ein.
- Für Januar 2010 angekündigt: ISBN 3527407243 oder 9783527407248 Signals and Systems Using SCILAB, Vorabinfo: kurzer Verlagstext PDF Seite 33 und bei Google-books.
- ISBN 9781584502814 (2004) Digital signal processing fundamentals mit einem sehr kleinen Anhang "Scilab Tutorial", sehr oberflächlich
- ISBN 9780817640095 (1999) Engineering and scientific computing with Scilab mit einem Kapitel zu "Signal Processing", für den Einstieg in Scilab sehr zu empfehlen. Auch als unveränderter Nachdruck von 2007 noch neu erhältlich.
Scilab-Berechnung mit eqiir
// Stopband-Filter für 1750 Hz, Samplerate =18029Hz
// Eckfrequenzen 1400Hz, 1700Hz, 1800 Hz, 2100Hz:
omega=[2*%pi*(1400/18029),2*%pi*(1700/18029),2*%pi*(1800/18029),2*%pi*(2100/18029)];
// Maximale Durchgangswelligkeit 0,5 dB
deltapass = (1-10**(-0.5/20)) ;
// minimale Sperrband-Dämpfung 50 dB
deltastop = 10**(-50/20);
// IIR-Filter berechnen, "stopband", "elliptic":
[sos,gain,zeroes,poles] = eqiir('sb','el',omega,deltapass,deltastop);
// Second order sections anzeigen:
sos
gain
//Frequenzgang berechnen und plotten:
zaehlerprodukt = prod(sos(2));
nennerprodukt = prod(sos(3));
frequenzgang = gain*abs(freq(zaehlerprodukt,nennerprodukt,exp(%i*(0:0.01:%pi))));
// frequenzgang = gain*abs(freq(zaehlerprodukt,nennerprodukt,exp(%i*(0:0.01:%pi))));
n = prod(size(frequenzgang));
//plot(20*log(frequenzgang(2:n))/log(10),(n*18029/(200*%pi)));
plot(20*log(frequenzgang (2:n))/log(10))
(Ergebnis:)
2 2 2
1 - 1.6219938z + z 1 - 1.6396794z + z 1 - 1.656616z + z
sos = -------------------------- * ------------------------ * -------------------------
2 2 2
0.9383702 - 1.5100165z + z 0.8466245 - 1.513936z + z 0.9485511 - 1.663563z + z
gain = 0.8683583
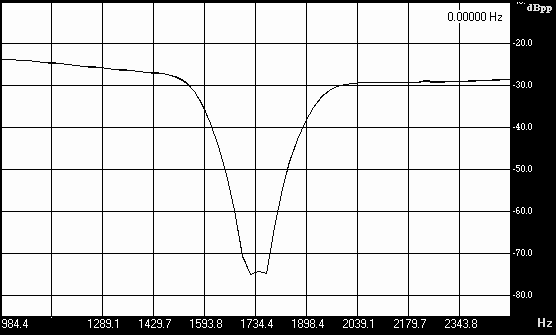
Messung des 1750 Hz-Sperrfilters
Gemessen mit "Visual Analyzer":
Frequenzgang-Planung mit Yulewalk
Oben das Programm, weitgehend aus dem Hilfetext entnommen, in der Mitte der berechnete Frequenzgang - Messung liegt noch keine vor -, unten rechts die Vorgabe mit Geradenstücken, links die Übertragungsfunktion 6.Ordnung.
Die Koeffizienten heißen im Zähler von links nach rechts b6...b0 , im Nenner a6...a0, wobei a0 immer =1 ist. Hier die Zerlegung in Teilfilter mit Octave:
B=[0.1211431 0.0379961 -0.0272326 -0.0361440 -0.0041574 -0.0010921 -0.0894734 ];
A=[1 -1.7641816 2.7032943 -2.3805502 1.8419165 -0.8344276 0.2958684];
[sos,g] = tf2sos(B,A)
//
// octave.exe:2> B=[0.1211431 0.0379961 -0.0272326 -0.0361440 -0.0041574 -0.0010921 -0.0894734 ];
// octave.exe:3> A=[1 -1.7641816 2.7032943 -2.3805502 1.8419165 -0.8344276 0.2958684];
// octave.exe:4> [sos,g] = tf2sos(B,A)
// sos =
//
// 1.0000000 1.1503168 1.0001280 1.0000000 0.0596667 0.7154071
// 1.0000000 -0.8390889 0.7389315 1.0000000 -0.7453174 0.7120574
// 1.0000000 0.0024186 -0.9993911 1.0000000 -1.0785309 0.5808050
//
// g = 0.12114
In drei Zeilen untereinander die drei Teilfilter-Koeffizienten, von links nach rechts b0, b1, b2, a0 (wieder=1), a1 und a2.
Quelltext des ATmega48-Programms
basierend auf AVR223, zerlegt in 3 SOS-Teilfilter, mit Überlaufbegrenzung
;***************************************************************************
;* Digital filter with ATmega48P 6th-order IIR, AVR223 application note *
;* 15 MHz xtal, input ADC0, PWM-output OCR1a/b, test output PD0 *
;* Christoph Kessler 2008 db1uq_at_t-online_dot_de *
;***************************************************************************
.nolist
.include "m48pdef.inc"
.list
;***************************************************************************
;* register 0-15 (no "immediate"-operations possible):
;***************************************************************************
.def MltLo = r0 ; multiplier result
.def MltHi = r1 ; multiplier result
.def Zero = r2 ; Zero register (used to add carry flag)
.def SavSrg = r3 ; save status register during interrupt routine
.def reg04 = r4 ; free
.def reg05 = r5 ; free
.def reg06 = r6 ; free
.def reg07 = r7 ; free
.def reg08 = r8 ; free
.def reg09 = r9 ; free
.def reg10 = r10 ; free
.def reg11 = r11 ; free
.def reg12 = r12 ; free
.def accu0 = r13 ; Accumulator - 32bit for Interrupt routine
.def accu1 = r14 ; Accumulator - 32bit for Interrupt routine
.def accu2 = r15 ; Accumulator - 32bit for Interrupt routine
;***************************************************************************
;* register 16-23 ("immediate"-operations possible):
;***************************************************************************
.def accu3 = r16 ; Accumulator - 32bit for Interrupt routine
.def reg17 = r17 ; free
.def reg18 = r18 ; free
.def reg19 = r19 ; free
.def datal = r20 ; Data samples mul register
.def datah = r21 ; for Interrupt routine
.def coefl = r22 ; Filter coefficient mul register
.def coefh = r23 ; for Interrupt routine
;***************************************************************************
;* register 24-31 (16Bit-registers)
;***************************************************************************
.def Tmp1 = r24 ; general temporary register
.def Tmp2 = r25 ; general temporary register
; XL = r26 ; free
; XH = r27 ; free
; YL = r28 ; used by Interrupt routine
; YH = r29 ; used by Interrupt routine
; ZL = r30 ; init routine only, free for main program
; ZH = r31 ; init routine only, free for main program
;*************************************************************************
;* constants :
;*************************************************************************
; 1st SOS filter
.equ x11 = 0
.equ x21 = 2
.equ y11 = 4
.equ y21 = 6
; 2nd SOS filter
.equ x12 = 8
.equ x22 = 10
.equ y12 = 12
.equ y22 = 14
; 3rd SOS filter
.equ x13 = 16
.equ x23 = 18
.equ y13 = 20
.equ y23 = 22
; 1st SOS filter
.equ b01 = 24
.equ b11 = 26
.equ b21 = 28
.equ a11 = 30
.equ a21 = 32
; 2nd SOS filter
.equ b02 = 34
.equ b12 = 36
.equ b22 = 38
.equ a12 = 40
.equ a22 = 42
; 3rd SOS filter
.equ b03 = 44
.equ b13 = 46
.equ b23 = 48
.equ a13 = 50
.equ a23 = 52
;*****************************************************
;* Macros
;*****************************************************
.MACRO load_node
ldd datal,Y+@0 ; Load low byte of node
ldd datah,Y+@0+1 ; Load high byte of node
.ENDMACRO
.MACRO update_node
std Y+@0,datal ; Update low byte of node to prepare next filter run
std Y+@0+1,datah ; Update high byte of node to prepare next filter run
.ENDMACRO
.MACRO load_coef
ldd coefl,Y+@0 ; Load low byte of node
ldd coefh,Y+@0+1 ; Load high byte of node
.ENDMACRO
.MACRO mul_move_32
muls coefh,datah ; Signed multiply, coefficient high byte and data high byte
mov accu2,MltLo ; Copy result word into accumulator byte 2:3
mov accu3,MltHi ; Copy result word into accumulator byte 2:3
mul coefl,datal ; Unsigned multiply, coefficient low byte and data low byte
mov accu0,MltLo ; Copy result word into accumulator byte 2:3
mov accu1,MltHi ; Copy result word into accumulator byte 2:3
mulsu coefh,datal ; Signed-unsigned multiply, coefficient high byte and data low byte
sbc accu3,Zero ; Sign extention
add accu1,MltLo ; Add low byte of result to accumulator byte 1
adc accu2,MltHi ; Add with carry high byte of result to accumulator byte 2
adc accu3,Zero ; Add carry to accumulator byte 3
mulsu datah,coefl ; Signed-unsigned multiply, data high byte and coefficient low byte
sbc accu3,Zero ; Sign extention
add accu1,MltLo ; Add low byte of result to accumulator byte 1
adc accu2,MltHi ; Add with carry high byte of result to accumulator byte 2
adc accu3,Zero ; Add carry to accumulator byte 3
.ENDMACRO
.MACRO smac32
muls coefh,datah ; Signed multiply, coefficient high byte and data high byte
add accu2,MltLo ; Add low byte of result to accumulator byte 2
adc accu3,MltHi ; Add with carry high byte of result to accumulator byte 3
mul coefl,datal ; Unsigned multiply, coefficient low byte and data low byte
add accu0,MltLo ; Add low byte of result to accumulator byte 0
adc accu1,MltHi ; Add with carry high byte of result to accumulator byte 1
adc accu2,Zero ; Add carry to accumulator byte 2
adc accu3,Zero ; Add carry to accumulator byte 3
mulsu coefh,datal ; Signed-unsigned multiply, coefficient high byte and data low byte
sbc accu3,Zero ; Sign extention
add accu1,MltLo ; Add low byte of result to accumulator byte 1
adc accu2,MltHi ; Add with carry high byte of result to accumulator byte 2
adc accu3,Zero ; Add carry to accumulator byte 3
mulsu datah,coefl ; Signed-unsigned multiply, data high byte and coefficient low byte
sbc accu3,Zero ; Sign extention
add accu1,MltLo ; Add low byte of result to accumulator byte 1
adc accu2,MltHi ; Add with carry high byte of result to accumulator byte 2
adc accu3,Zero ; Add carry to accumulator byte 3
; ret
.ENDMACRO
.LISTMAC
;*************************************************************************
;* reset/interrupt-vectors:
;*************************************************************************
.cseg
rjmp Initial ; after RESET to main program
reti ; External Interrupt Request 0
reti ; External Interrupt Request 1
; reti ; External Interrupt Request 2 mega644
reti ; Pin Change Interrupt Request 0
reti ; Pin Change Interrupt Request 1
reti ; Pin Change Interrupt Request 2
; reti ; Pin Change Interrupt Request 3 mega644
reti ; Watchdog Time-out Interrupt
reti ; Timer/Counter2 Compare Match A
reti ; Timer/Counter2 Compare Match B
reti ; Timer/Counter2 Overflow
reti ; Timer/Counter1 Capture Event
reti ; Timer/Counter1 Compare Match A
reti ; Timer/Counter1 Compare Match B
reti ; Timer/Counter1 Overflow
reti ; Timer/Counter0 Compare Match A
reti ; Timer/Counter0 Compare Match B
reti ; Timer/Counter0 Overflow
reti ; SPI Serial Transfer Complete
reti ; USART0, Rx Complete
reti ; USART0 Data register Empty
reti ; USART0, Tx Complete
; reti ; Analog Comparator mega644
rjmp ADCint ; ADC Conversion Complete
reti ; EEPROM Ready
reti ; 2-wire Serial Interface
reti ; Store Program Memory Read
;*************************************************************************
;* after reset: initialise stack,ports
;*************************************************************************
Initial:
ldi Tmp1,Low(RAMEND)
out SPL,Tmp1 ;
ldi Tmp1,High(RAMEND)
out SPH,Tmp1 ; stack initialised
clr Zero ; always Zero
ldi Tmp1,$FF ;
out PortB,Tmp1 ; PortB = % 1111 1111
out PortC,Zero ; PortC = % 0000 0000
out PortD,Tmp1 ; PortD = % 1111 1111
out DDRB,Tmp1 ; PortB direction = % 1111 1111
out DDRC,Zero ; PortC direction = % 0000 0000
out DDRD,Tmp1 ; PortD direction = % 1111 1111
ldi Tmp1,$A1 ; pos. outputs, fast PWM 8Bit
sts TCCR1A,Tmp1 ;
ldi Tmp1,$09 ; fast PWM 8Bit, clk/1 (no prescaling)
sts TCCR1B,Tmp1 ;
sts OCR1AH,Zero ;
sts OCR1AL,Zero ;
sts OCR1BH,Zero ;
sts OCR1BL,Zero ;
ldi Tmp1,$40 ; Ref=Vcc, right-adj, ADC0=input
sts ADMUX,Tmp1 ;
; ldi Tmp1,$EE ; Start,Auto, enable Int, Clk/64
ldi Tmp1,$EF ; Start,Auto, enable Int, Clk/128
sts ADCSRA,Tmp1 ;
ldi Tmp1,$00 ; free running
sts ADCSRB,Tmp1 ;
ldi Tmp1,$01 ; disable ADC0 dig.inp (optional)
sts DIDR0,Tmp1 ;
ldi ZL,low(CoTblF<<1) ; move filter coefficents
ldi ZH,high(CoTblF<<1) ; from program-flash
ldi YL,low(CoTblS) ; to SRAM
ldi YH,high(CoTblS) ;
ldi Tmp1,30 ; count 15 * 16 Bit coefficients
TbLoop:
lpm Tmp2,Z+ ; fetch 1 byte from coefficient table
st Y+,Tmp2 ; copy coefficient to Sram, increment Y
dec Tmp1
brne TbLoop
ldi YL,low(DatTbl) ; load SRAM-Pointer for Interrupt routine
ldi YH,high(DatTbl) ;
sei ; enable interrupts
;*************************************************************************
;* Main program:
;*************************************************************************
Endless:
rjmp Endless ;
;*************************************************************************
;* ADC-Interrupt routine: compute filter and update PWM output
;*************************************************************************
ADCint:
sbi PortD,0 ; just to measure INT-Time
in SavSrg,SREG ; save status register
;*************************************************************************
;* 1st SOS filter
;*************************************************************************
load_coef b21 ; b21*x1[t-2]
load_node x21 ;
mul_move_32 ;
load_coef b11 ; b11*x1[t-1]
load_node x11 ;
update_node x21 ;
smac32 ;
load_coef b01 ; b01*x1[t]
lds datal,ADCL ; Load new sample
lds datah,ADCH ; into data multiply register
dec datah ; convert 10 bit unsigned $03FF -> $01FF
dec datah ; to 16 Bit signed $0000 -> $FE00
lsl datal
rol datah
lsl datal
rol datah
lsl datal
rol datah
lsl datal
rol datah
lsl datal
rol datah
lsl datal
rol datah
update_node x11 ;
smac32 ;
load_coef a21 ; a21*y1[t-2]
load_node y21 ;
smac32 ;
load_coef a11 ; a11*y1[t-1]
load_node y11 ;
update_node y21 ;
smac32 ;
cpi accu3,$20 ; accu < $20000000 ?
brlo NoLimit1 ;
cpi accu3,-$20 ; accu >= -$20000000 ?
brsh NoLimit1 ;
clr accu2 ; accu2 = $00
cpi accu3,0 ;
brge PosLim1 ;
ldi accu3,$80 ; accu3 = $80
rjmp Limit1 ;
PosLim1:
ldi accu3,$7F ; accu3 = $7F
com accu2 ; accu2 = $FF
rjmp Limit1 ;
NoLimit1:
lsl accu1 ; Scaling to gain factor 2^15
rol accu2 ;
rol accu3 ;
lsl accu1 ; Scaling to gain factor 2^16
rol accu2 ;
rol accu3 ;
Limit1:
std Y+y11,accu2 ; Updating y1[t-1] node to prepare next filter run
std Y+y11+1,accu3 ; and save it for following SOS filter
;*************************************************************************
;* 2nd SOS filter
;*************************************************************************
load_coef b22 ; b22*x2[t-2]
load_node x22 ;
mul_move_32 ;
load_coef b12 ; b12*x2[t-1]
load_node x12 ;
update_node x22 ;
smac32 ;
load_coef b02 ; b02*x2[t]
load_node y11 ; result of 1st SOS
update_node x12 ;
smac32 ;
load_coef a22 ; a22*y2[t-2]
load_node y22 ;
smac32 ;
load_coef a12 ; a12*y2[t-1]
load_node y12 ;
update_node y22 ;
smac32 ;
cpi accu3,$20 ; accu < $20000000 ?
brlo NoLimit2 ;
cpi accu3,-$20 ; accu >= -$20000000 ?
brsh NoLimit2 ;
clr accu2 ; accu2 = $00
cpi accu3,0 ;
brge PosLim2 ;
ldi accu3,$80 ; accu3 = $80
rjmp Limit2 ;
PosLim2:
ldi accu3,$7F ; accu3 = $7F
com accu2 ; accu2 = $FF
rjmp Limit2 ;
NoLimit2:
lsl accu1 ; Scaling to gain factor 2^15
rol accu2 ;
rol accu3 ;
lsl accu1 ; Scaling to gain factor 2^16
rol accu2 ;
rol accu3 ;
Limit2:
std Y+y12,accu2 ; Updating y2[t-1] node to prepare next filter run
std Y+y12+1,accu3 ; and save it for following SOS filter
;*************************************************************************
;* 3rd SOS filter
;*************************************************************************
load_coef b23 ; b23*x3[t-2]
load_node x23 ;
mul_move_32 ;
load_coef b13 ; b13*x3[t-1]
load_node x13 ;
update_node x23 ;
smac32 ;
load_coef b03 ; b03*x3[t]
load_node y12 ; result of 2nd SOS
update_node x13 ;
smac32 ;
load_coef a23 ; a23*y3[t-2]
load_node y23 ;
smac32 ;
load_coef a13 ; a13*y3[t-1]
load_node y13 ;
update_node y23 ;
smac32 ;
cpi accu3,$20 ; accu < $20000000 ?
brlo NoLimit3 ;
cpi accu3,-$20 ; accu >= -$20000000 ?
brsh NoLimit3 ;
clr accu2 ; accu2 = $00
cpi accu3,0 ;
brge PosLim3 ;
ldi accu3,$80 ; accu3 = $80
rjmp Limit3 ;
PosLim3:
ldi accu3,$7F ; accu3 = $7F
com accu2 ; accu2 = $FF
rjmp Limit3 ;
NoLimit3:
lsl accu1 ; Scaling to gain factor 2^15
rol accu2 ;
rol accu3 ;
lsl accu1 ; Scaling to gain factor 2^16
rol accu2 ;
rol accu3 ;
Limit3:
std Y+y13,accu2 ; Updating y3[t-1] node to prepare next filter run
std Y+y13+1,accu3 ;
;*************************************************************************
;* PWM - D/A-output
;*************************************************************************
subi accu3,$80 ; signed to unsigned $8000 ->$0000, $7FFF ->$FFFF
sts OCR1AH,Zero ;
sts OCR1AL,Tmp1 ; fast PWM 8 bit input signal to OCR1A
sts OCR1BH,Zero ;
sts OCR1BL,accu3 ; fast PWM 8 bit result to OCR1B
cbi PortD,0 ; just to measure INT-Time
out SREG,SavSrg ; restore status register
reti ;
;*************************************************************************
;* coefficient table in flash memory
;*************************************************************************
CoTblF:
/*
;1750 Hz Sperrfilter:
.dw 16384 ; b01 *16384 ( 1 )
.dw -26575 ; b11 *16384 (-1,6219938)
.dw 16384 ; b21 *16384 ( 1 )
.dw 24740 ; -a11 *16384 ( 1,5100165)
.dw -15374 ; -a21 *16384 (-0,9383702)
.dw 16384 ; b02 *16384 ( 1 )
.dw -26865 ; b12 *16384 (-1,6396794)
.dw 16384 ; b22 *16384 ( 1 )
.dw 24804 ; -a12 *16384 ( 1,5139300)
.dw -13871 ; -a22 *16384 (-0,8466245)
.dw 16384 ; b03 *16384 ( 1 )
.dw -27142 ; b13 *16384 (-1,6566160)
.dw 16384 ; b23 *16384 ( 1 )
.dw 27256 ; -a13 *16384 ( 1,6635630)
.dw -15541 ; -a23 *16384 (-0,9485511) */
;SSTV-Bandpass nach DJ6HP 015:
.dw 16384 ; b01 *16384 ( 1 )
.dw 18847 ; b11 *16384 ( 1.1503168)
.dw 16386 ; b21 *16384 ( 1.0001280)
.dw -978 ; -a11 *16384 (-0.0596667)
.dw -11721 ; -a21 *16384 (-0.7154071)
.dw 16384 ; b02 *16384 ( 1 )
.dw -13748 ; b12 *16384 (-0.8390889)
.dw 12107 ; b22 *16384 ( 0.7389315)
.dw 12211 ; -a12 *16384 ( 0.7453174
.dw -11666 ; -a22 *16384 (-0.7120574)
;
.dw 16384 ; b03 *16384 ( 1 )
.dw 40 ; b13 *16384 ( 0.0024186)
.dw -16374 ; b23 *16384 (-0.9993911)
.dw 17671 ; -a13 *16384 ( 1.0785309)
.dw -9516 ; -a23 *16384 (-0.5808050)
;*************************************************************************
;* data memory in SRAM
;*************************************************************************
.dseg
.org $0100
DatTbl:
.dw $0000 ; x11
.dw $0000 ; x21
.dw $0000 ; y11
.dw $0000 ; y21
;
.dw $0000 ; x12
.dw $0000 ; x22
.dw $0000 ; y12
.dw $0000 ; y22
;
.dw $0000 ; x13
.dw $0000 ; x23
.dw $0000 ; y13
.dw $0000 ; y23
;*************************************************************************
;* coefficient table in SRAM
;*************************************************************************
CoTblS:
.dw $0000 ; b01 *16384
.dw $0000 ; b11 *16384
.dw $0000 ; b21 *16384
.dw $0000 ; -a11 *16384
.dw $0000 ; -a21 *16384
;
.dw $0000 ; b02 *16384
.dw $0000 ; b12 *16384
.dw $0000 ; b22 *16384
.dw $0000 ; -a12 *16384
.dw $0000 ; -a22 *16384
;
.dw $0000 ; b03 *16384
.dw $0000 ; b13 *16384
.dw $0000 ; b23 *16384
.dw $0000 ; -a13 *16384
.dw $0000 ; -a23 *16384
;*************************************************************************