GhostCarProjekt
von and_ref
Dieser Artikel nimmt am Artikelwettbewerb 2012/2013 teil.
GCP - das GhostCarProjekt...
... steht als Projekttitel für die Realisierung eines autonom fahrenden Fahrzeugs auf einer spurgebundenen Spielzeugrennbahn. Es soll ein Auto entwickelt werden, das auf einer Carrerabahn möglichst schnelle Rundenzeiten fährt. Dabei sind Eingriffe in die Strecke oder Steuerbefehle von außen tabu.
Idee und Motivation
Die legendäre Carrerabahn aus Kindheitstagen ist vielen noch ein Begriff. Die Hauptmerkmale sind steckbare Schienenteile mit Führungsschlitz in der Mitte und zwei Spannungsschienen, die die für den Elektromotor nötige Energie liefern. Für manuell gesteuerte Autos wird durch einen Handregler der Schienensstrom (Analogbahn) oder ein PWM-Datenwort (Digitalbahn) vorgegeben und damit die Fahrgeschwindigkeit gesteuert. Für Digitalbahnen gibt es von Carrera unter dem Begriff Ghostcar auch automatisch fahrende Fahrzeuge. Diese fahren mit einer konstanten Geschwindigkeit, die manuell auf die langsamsten Stelle auf der Strecke eingerichtet wird. Aber erst wenn das Fahrzeug auch auf Geraden schneller fährt und rechtzeitig vor Kurven abbremst, verhält sich das Ghostcar wie ein realer Gegner. Genau dies soll das Gcp-Fahrzeug (hier dann als Abkürzung für GhostCar Protoyp) leisten können.
Konzept
Grundprinzip
Der entscheidende Punkt um schnell fahren zu können ist das Wissen über den Streckenverlauf und die Position des Autos auf der Strecke. Hierzu wurde ein Carrera-Auto mit einem Gyrosensor und einer Reflexkoppler-Lichtschranke an der Hinterachse ausgestattet. Der Gyrosensor misst die Winkelgeschwindkeit (in Milligrad pro Sekunde [mdps]), oder anders formuliert, er liefert einen Wert, der aussagt, wie schnell sich das Fahrzeug um seine Hochachse dreht - im folgenden als GyroZ bezeichnet. Misst man sehr häufig und summiert alle Zahlenwerte auf, so ergibt sich daraus der zurückgelegte Kurvenwinkel (oder mathematisch ausgedrückt: Der überstrichene Winkel ist das Integral der Drehrate).
Mit der Reflexkoppler-Lichtschranke, die eine Scheibe mit schwarzen und weißen Teilungsstrichen abtastet, lassen sich (Teil-)Umdrehungen der hinteren Antriebsräder messen. Werden die gezählten "Wheelticks" durch eine (Tor-)Zeit dividiert, so erhält man daraus die Raddrehzahl (gemessen in RPM). Sofern kein Schlupf an den Rädern auftritt, ist die Fahrzeuggeschwindigkeit proportional zur Raddrehzahl.
Wie können die aufgenommenen Messwerte ausgewertet werden?
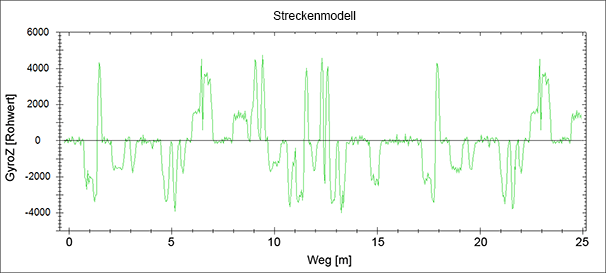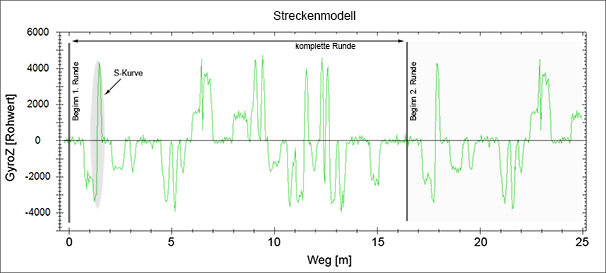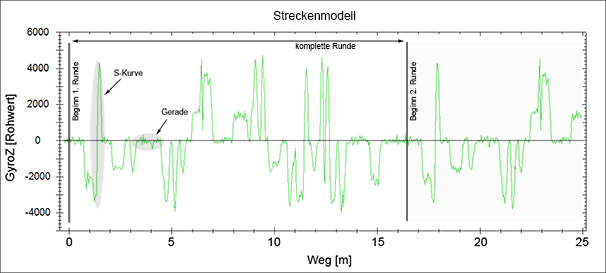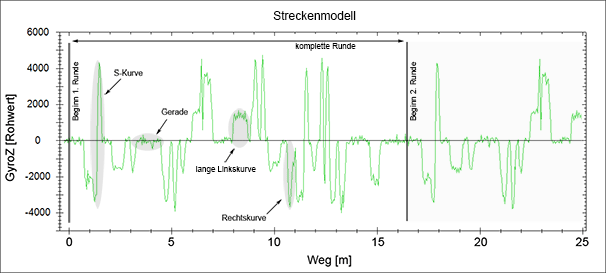
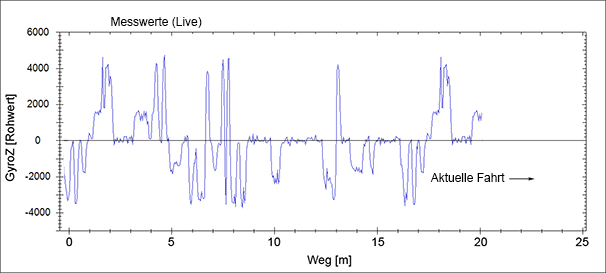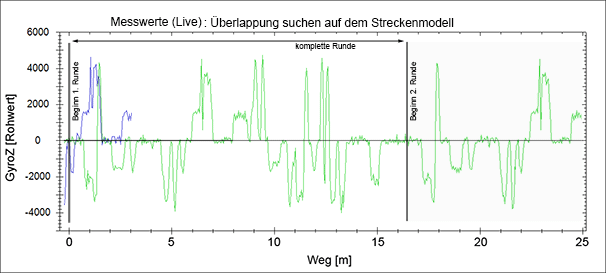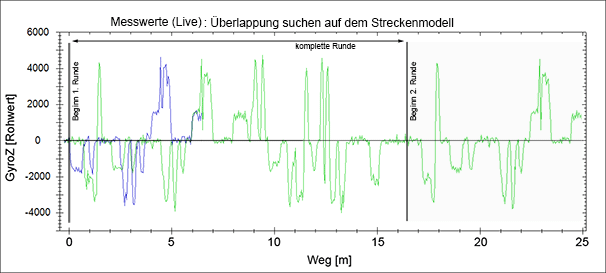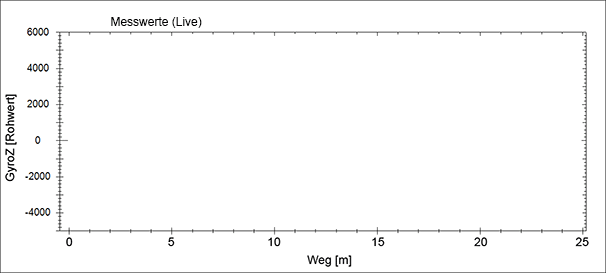
Die nachfolgende Animation zeigt einen aufgezeichneten GyroZ-Verlauf einer kompletten Runde (plus etwas Zugabe).
Diese Strecke besteht aus 14 Rechts- und 9 Linkskurven unterschiedlicher Kurvenradien und -längen. Ein hoher GyroZ-Wert bedeutet (bei konstanter Geschwindigkeit) eine hohe Drehrate und damit einen engen Kurvenradius. Kleinere GyroZ-Werte bedeuten weniger enge Kurven. Die plateauartigen Passagen sind Teilstücke, die eine konstante Drehrate über eine längere Zeit (bzw. Weg) haben, z.B. langgezogene Kurven oder Geraden. Kurze Kurven oder kurze Geraden werden durch kurze Peaks abgebildet.
Normiert man den GyroZ-Wert auf eine Geschwindigkeit von z.B. 1000RPM (=> GyroZNorm = Rohwert / Drehzahl * 1000), so erhält man eine von der Momentangeschwindigkeit unabhängige Aussage über den Kurvenradius.
Die dargestellten Daten sind bereits umgerechnet auf den zurückgelegten Weg (anstatt den GyroZ-Verlauf über der Zeit darzustellen). Dies hat den Vorteil, dass man so immer den gleichen Kurvenverlauf erhält - egal, ob man langsam oder schnell fährt. Dieser Kurvenverlauf ist also ein charakteristischer Verlauf der Strecke und nicht der momentanen Fahrweise. Somit ist der genaue Verlauf der Strecke bekannt, es liegt quasi ein Streckenmodell vor - bitte in Gedanken auf Karton ausdrucken.
Stellt man sich jetzt weiter vor, dass das Auto schon einen längeren Weg auf dieser Strecke zurückgelegt hat und sich gerade irgendwo mitten in der Runde befindet, könnte man den aktuellen GyroZ-Verlauf bis hierhin auf ein (ggf. sehr) breites Stück Transparentpapier drucken. Würde man dieses Transparentpapier beliebig über den Karton vom Streckenmodell legen, so könnte man durch hin- und herschieben des Transparentpapiers, beide Kurvenverläufe zur Deckung bringen. Dort wo der rechte Rand des Papiers ist, dort befindet man sich gerade (bezogen auf das Streckenmodell). Um zu wissen ob beschleunigt werden darf oder ob gebremst werden muss, muss man nur auf dem Streckenmodell (Karton) etwas nach rechts schauen (also quasi in die Zukunft blicken) und kann sich so auf den weiteren Streckenverlauf einstellen. Die nachfolgende Animation soll das prinzipielle Vorgehen verdeutlichen.
Animation: Positionsermittlung
In der Signalverarbeitung läuft das Verfahren des Übereinanderschiebens unter dem Begriff Autokorrelation. Liegen alle Messwerte gleichzeitig vor, so kann nach vielen Rechenschritten ausgesagt werden, wie die beiden Papiere zueinander geschoben werden müssen, um deckungsgleich zu sein, sprich, wo sich die Momentanposition auf dem Streckenmodell befindet.
Allerdings liegt an dieser Stelle auch das Problem: Es sind weder alle Messdaten gleichzeitig(!) vorrätig (mangels RAM), noch steht genügend Rechenzeit zur Verfügung, um alle Verschiebungen durchrechnen zu können.
Abschätzung der anfallenden Datenmenge: Messrate 1kHz; Rundenlänge 20s => 40kByte pro Runde
Abschätzung der Rechenzeit: Näherungsweise eine Addition und eine Multiplikation (je 16bittig) pro Millisekunde UND pro Durchgang => 500ns * 20s * 1000[1/s] * 20.000 = 200s.
Um die Position fortlaufend bestimmen zu können, müsste man diese Rechnung mehrmals pro Sekunde abschließen können. So lässt sich dieses Verfahren also nicht umsetzen - es muss effizienter durchgeführt werden.
Übertragung des Grundprinzips in eine ressourcenschonende Implementierung
Dieser Abschnitt gibt nur einen kurzen Überblick über die grundlegenden Verarbeitungsschritte im Fahrzeug. Alle verwendeten Algorithmen und Ideen werden danach genauer unter die Lupe genommen.
Das folgende Diagramm soll den Ablauf grob skizzieren:
Sektorerkennung: Streckenaufteilung in Sektoren zur Datenverdichtung
Wenn man sich die GyroZ-Verläufe genau ansieht stellt man fest, dass sich immer Abschnitte finden lassen, in denen der GyroZ-Wert für eine gewisse Zeit stabil ist. Eigentlich ist der Verlauf fast eine Rechteckkurve. Das liegt an den Carrera Schienenteilen, die konstante Kurvenradien haben (es gibt keine parabelförmigen Kurven o.ä.). Dies lässt sich gut ausnutzen, um Abschnitte bzw. Sektoren zu bilden. Eingeschränkt gilt dies auch für frei verlaufende, "organische" Bahnverläufe.
Ein Sektor ist also ein Streckenabschnitt, dessen GyroZ-Verlauf nahezu konstant ist. Als Sektorparameter reicht es also aus, wenn nur der charakteristische GyroZ-Wert und die Sektorlänge gespeichert wird, um später daraus wieder den eigentlichen GyroZ-Verlauf rekonstruieren zu können. Dies gilt sowohl für Kurven, als auch für Geraden (bei denen der GyroZ-Wert ~0 ist). So lässt sich unsere Beispielstrecke "GcpShort1" in ca. 31 Sektoren zerlegen, siehe Bild rechts. (Hinweis: Die Farben kennzeichnen den Kurvenradius und sollen die Strecke nicht in einzelne Sektoren teilen). Der benötigte Speicherbedarf ist mit weniger als 400Bytes (=MaxAnz Sektoren * 4Parameter zu je 16Bit; Details später) durchaus µC-tauglich.
Wie lassen sich aus dem kontinuierlichen Messdatenstrom Sektoren bestimmen?
Stellt man sich ein virtuelles horizontales Band um den GyroZ-Verlauf vor und legt fest, dass ein Sektor endet, sobald der GyroZ-Wert (für eine gewisse Zeit) die Bandgrenzen überschreitet, dann erhält man automatisch eine Stückelung in Abschnitte/Sektoren, die als Gemeinsamkeit einen ähnlichen GyroZ-Wert haben.
Wenn man die Bandhöhe (also die Höhe des gewählten Bandes) so wählt, dass nicht zu viele Kleinstsektoren oder nichtaussagekräftige Großsektoren entstehen, hat man automatisch eine gute Annäherung an den tatsächlichen (kontinuierlichen) GyroZ-Verlauf und muss nur ein Bruchteil der anfallenden Daten vorhalten.
Aber wie und wann legt man sich auf die Bandmitte fest, um die letztendlich das Band gelegt wird? Die Praxis zeigt, dass sich der GyroZ-Wert nach kurzer Zeit auf sein neues stabiles Plateau einpendelt - und zwar relativ unabhängig von der Lage/Höhe des Plateaus. Man nimmt z.B. 75ms nach Sektorbeginn einfach den GyroZ-Wert heraus, der gerade anliegt und definiert diesen zur aktuellen Bandmitte für den gerade aktiven Sektor. Praktisch verbessert sich die Sektorqualität noch etwas, wenn man nicht den letzten Rohwert nimmt, sondern einen leicht gefilterten GyroZ-Wert heranzieht (PT1-Filter mit 100ms Filterzeit). Ignoriert man dann noch kurze Ausreißer aus dem Band, die z.B. wegen Messfehlern/-schwankungen vorkommen, dann erhält man relativ saubere Sektordaten, die den physikalischen Gegebenheiten bei langsamer Fahrt ziemlich genau entsprechen.
Möchte man die Sektordaten dann nutzen, um die eigene Position auf der Strecke zu berechnen, und zeichnet daraus einen GyroZ-Verlauf, so lässt sich theoretisch genauso vorgehen wie oben mit den (quasi)kontinuierlichen Messwerten beschrieben (Stichwort: Autokorrelation; Verschieben der Papiere). Praktisch würde man dann die aktuellen Sektordaten mit vergangenen Sektordaten vergleichen und bei einer erkannten, identischen Folge könnte man auf die aktuelle Position schließen. Doch leider funktioniert dies so nicht ausreichend genau, da die Sektorgrenzen nicht immer am gleichen physikalischen Ort auf der Strecke liegen (also z.B. nicht genau am Kurveneingangspunkt), weil die "Vorgeschichte" des GyroZ-Verlaufs in die Wahl der Bandmitte einfließt und sich somit der Zeitpunkt (und auch Ort) des Bandverlassens verschiebt => Bremspunkt verschiebt sich => Abflug garantiert. Zudem ändern sich die Sektordaten deutlich, wenn sich die Fahrzeuggeschwindigkeit ändert. Es kommt bei höheren Geschwindigkeiten zu Drifts und Überschwingern. Dies führt zu "zufällig" auftauchenden Sektoren, die die Positionsbestimmung zusätzlich erschwert. Überschwinger treten z.B. am Kurvenausgang auf, wenn das Fahrzeug weiter seiner Kurvenbahn folgen möchte, obwohl die Strecke bereits in die Gerade übergegangen ist (Massenträgheit). Das führt dann dazu, dass die Sektordaten suggerieren, dass die Kurve länger erscheint als sie es tatsächlich ist. Der Kurvenausgangspunkt verschiebt sich so vermeintlich. Bei S-Kurven ist die Sache noch extremer. Hier hängen die Sektordaten noch stärker von der Fahrzeuggeschwindigkeit ab. Praxisbeispiel: Unsere Beispielstrecke ist bei langsamer Geschwindigkeit (1.5m/s = 1285RPM) ungefähr 30.4m lang. Bei leicht höherer Geschwindigkeit (2m/s = 1700RPM) ist die vom Fahrzeug gemessene Streckenlänge schon 31m! (Die Reproduzierbarkeit der Streckenlänge bei konstanter Geschwindigkeit beträgt unter 10cm). Die Abweichung kommt durch die angesprochenen Drifts zustande, aber auch durch "Abkürzen" von S-Kurven bei langsamer Fahrt.
Alles in allem also keine guten Voraussetzungen für eine schnelle und sichere Fahrt. Dennoch liefern diese Sektordaten einen wichtigen Beitrag zum Streckenmodell und werden deswegen unbedingt benötigt. Die Länge aller Geraden wird ausreichend zuverlässig ermittelt, auch die Länge und Radien der Kurvenstücke ist gut genug, um daraus eine maximal mögliche Fahrgeschwindigkeit abzuleiten. Lediglich die Reproduzierbarkeit bzw. der genaue physikalische Ort der Sektorgrenzen ist verbesserungswürdig.
Was sind weiße/schwarze Sektoren und wie kann die Qualität der Sektordaten verbessert werden?
Um die Reproduzierbarkeit zu erhöhen, muss zusätzlich auf ein weiteres Verfahren zur Ermittlung von Sektorkenngrößen gesetzt werden. Um sprachlich hier nicht die beiden Konzepte zu vermischen, nennen wir die beiden Verfahren zur Sektorerkennung:
- Konzept "Band verlassen" oder "weißer Algorithmus bzw. weiße Sektordaten"
- Konzept "Charakteristische Stellen" oder "schwarzer Algorithmus bzw. schwarze Sektordaten"
Das Konzept "Band verlassen/weiße Sektoren" ist oben bereits beschrieben. Im folgenden wird der schwarze Algorithmus näher betrachtet. Übrigens, die Begriffe sind willkürlich gewählt und sollen rein zur Unterscheidung dienen.
Ziel des schwarzen Algorithmus ist es die Sektorgrenzen an einen festen Ort zu binden. Das Auto muss sich darauf verlassen können, dass der Bremspunkt korrekt sitzt. Kurvenradien zu erfassen oder besonders gute Abbildung des GyroZ-Verlaufs sind hier also nicht gefragt.
Schaut man sich den GyroZ-Verlauf an einem Kurveneingang an, so fällt auf, dass dieser zunächst nahe 0 liegt und sich anschließend rampenförmig oder schon fast sprungförmig ändert. Kein Wunder, schließlich geht es ja von einer Geraden in eine Kurve über. Zur Erinnerung, die Carrera Schienenteile haben keinen weichen stetigen Übergang von Gerade in Kurve, sondern eine "unstetige Stelle". Aber selbst bei weichen Übergängen wäre ein Knick bzw. steiler Anstieg des GyroZ-Wertes vorhanden. Wenn man sich den Punkt merkt, bei dem der GyroZ-Wert ein gedachtes Nullband verlässt (auch hier wieder ein virtuelles Band um die Nulllinie vorstellen), dann sollte dieser Punkt in jeder Runde örtlich genau an der gleichen Stelle liegen. Am Ende einer (langen) Geraden fährt das Auto immer schnurgeradeaus. Um aber nicht Messrauschen oder kurzzeitige Schläge (z.B. durch die Stoßstellen der Schienen) fehlzuinterpretieren, wird verlangt, dass nach Abbiegen auch mindestens eine Kurve von 3° gefahren werden muss, sonst wird der Kurveneinlenkpunkt verworfen. Wurden aber die 3° "angesammelt", so gilt der Einlenkpunkt als Beginn eines neuen Sektors. Dieser Sektor endet erst wieder, wenn der GyroZ-Wert wieder ins Nullband zurückfällt UND es erneut verlässt (dabei natürlich wieder mehr als 3° überfährt).
Dadurch sind die schwarzen Sektoren nicht im geringsten mit den weißen Sektoren vergleichbar. Vereinfacht gesagt, beginnen und enden die schwarzen Sektoren immer an einem Übergang von Gerade in Kurve oder in S-Kurven. Dazwischen können aber beliebig viele andere Kurvenabschnitte liegen. Dies trifft auch für Kurven zu, deren Kurvenradius sich durch Aneinanderreihung von z.B. immer enger werdenden Schienenteilen ändert. Weiße Sektoren würden zu jeden einzelnen Schienenabschnitt einen Sektor liefern, der schwarze Sektor hingegen fasst diese alle zusammen.
Speichert man die weißen und schwarzen Sektordaten in zwei voneinander getrennten Listen, so erhält man für die Beispielstrecke folgende (idealisierte!) Tabellen:
| SektorNr | Sektorlänge | Sektorwinkel | Bandmitte | WegpunktAbs |
|---|---|---|---|---|
| 0 | 0.00m | 0° | 0[raw] | 0.00m |
| 1 | 2.00m | 0° | 0[raw] | 2.00m |
| 2 | 0.70m | -90° | -2200[raw] | 2.70m |
| 3 | 0.30m | -60° | -3500[raw] | 3.00m |
| 4 | 0.25m | +60° | 3800[raw] | 3.25m |
| 5 | 1.00m | 0° | 0[raw] | 4.25m |
| 6 | 0.90m | -90° | -1700[raw] | 5.15m |
| 7 | 0.60m | 0° | 0[raw] | 5.75m |
| 8 | 0.30m | -15° | -1600[raw] | 6.05m |
| 9 | 2.10m | 0° | 0[raw] | 8.15m |
| 10 | ... |
| SektorNr | Sektorlänge | Sektorwinkel | Kurvenlage | WegpunktAbs | Bezogen auf "weiß" |
|---|---|---|---|---|---|
| 0 | 0.00m | 0° | 0° | 0.00m | Initialsektor |
| 1 | 2.00m | 0° | 0° | 2.00m | S1 |
| 2 | 1.00m | -150° | -150° | 3.00m | S2+S3 |
| 3 | 1.25m | +60° | -90° | 4.25m | S4+S5 |
| 4 | 1.50m | -90° | -180° | 5.75m | S6+S7 |
| 5 | 2.40m | -15° | -195° | 8.15m | S8+S9 |
| 6 | ... |
Die weißen Sektoren dienen fortan ausschließlich als Streckenmodell. Die schwarzen Sektoren werden zur Synchronisierung/Positionsbestimmung verwendet. So kombinieren sich die Vorteile beider Sektorarten.
Positionsbestimmung/Synchronisierung
Unsere erste Idee (die sich später allerdings als Sackgasse herausstellte), war es, zu Beginn eine Referenzrunde zu fahren. Die weißen Sektoren sollten das Streckenmodell (Referenzsektorliste) bilden. Später sollte dann nur noch ermittelt werden, wo wir uns momentan (bezogen auf die Referenzrunde) befinden. Da sich die Sektoren aber stark in Abhängigkeit der Fahrzeuggeschwindigkeit ändern, war das Streckenmodell schon veraltet, bevor es überhaupt genutzt werden konnte. Außerdem müsste zuverlässig erkannt werden können, wann die Referenzrunde zu Ende sein soll. Auch musste der gerade erfahrene Livesektor eindeutig einem Referenzrundensektor zuordenbar sein, wollte man die Synchronität nicht verlieren. Das Vorgehen hätte dann so ausgesehen: Die Referenzfahrt liegt als komplette Liste vor und beinhaltet alle Sektoren der Runde. Der zuletzt gemeldete Sektor wird auf der Referenzsektorliste gesucht. Es wäre keine Liste mit aktuellen Sektordaten erforderlich gewesen. Nachteil: Würde auch nur eine Synchronisierung fehlschlagen, dann müsste die komplette Referenzfahrt erneut durchgeführt werden, da keine Infos über die letzten aufgelaufenen Sektoren vorlägen.
Als wesentlich geeigneter erwies sich das fortlaufende Aktualisieren nur einer Sektorliste nach dem FIFO-Prinzip. Einzige Bedingung: Die Runde darf nicht mehr Sektoren liefern, wie die Liste aufnehmen kann. Was natürlich die maximale Rundenlänge begrenzt, aber auch sicherstellt, dass immer die aktuellsten Daten vorliegen. Die Fahrt beginnt also mit einer Lernphase, deren einziger Zweck es ist, die Sektorliste zu füllen. Sobald dies erreicht ist, geht die Fahrt nahtlos in die eigentliche Ghostcarfahrt über und die Positionsbestimmung kann mit ihrer Arbeit beginnen. Ab jetzt wird schnell gefahren. (Derzeit umfasst die Liste 30 schwarze Sektoren, was auch für längere Strecken ausreicht).
Ziel: Es muss ausgehend vom aktuellen Sektor, der Vergleichssektor gefunden werden, der zu dem Streckenabschnitt vor genau einer Runde passt. Kurzum: "Der Vorrundensektor muss gefunden werden". Die Positionsbestimmung wird immer dann ausgeführt, wenn ein neuer Sektor von der Sektorerkennung angeliefert wird. Wenn die Positionsbestimmung zustandslos arbeitet, d.h. keine Infos aus vorangegangenen Synchronisationen für die aktuelle Rechnung benötigt, dann kann es auch nicht zu unheilbaren Fehlsynchronisationen kommen. Würde man auf dem Wissen aus den SyncRechnungen aus den vorherigen Sektoren aufbauen, so könnte man sich in eine Sackgasse manövrieren, aus der man (algorithmisch) nur schwer wieder heraus kommt.
Auf der Suche nach dem Vorrundensektor wird nicht einfach nur die gleiche Abfolge der letzten angefallenen Sektoren in der Sektorliste gesucht - da dies voraussetzen würde, dass die genaue Reihenfolge ohne Lücken und zusätzlichen Sektoren bereits so in der Liste steht. Wäre auch nur ein Sektor (z.B. wegen Überschwingern) hinzugekommen, dann käme der Algorithmus aus dem Tritt. Die Suche muss also robust gegen ausfallende bzw. zusätzliche Sektoren sein. Durch eine Ähnlichkeitssuche/Heuristik wird nicht die Reihenfolge der angefallenen Sektoren bewertet, sondern es wird versucht den Vorrundensektor über unabhängige Wahrscheinlichkeiten zu finden. Und das ist ganz ohne Sonderbehandlung zusätzlicher oder ausgefallener Sektoren möglich.
Heuristik: Wie lässt sich der Vorrundensektor zuverlässig aufspüren?
Getreu dem Motto "Wir können zwar nicht ausrechnen wo wir genau sind, dafür schätzen wir aber recht gut", setzen wir für die Positionsbestimmung ein heuristisches Verfahren ein. Eine statistische Auswertung der in Frage kommenden Vorrundensektoren soll uns dabei helfen. Alle nachfolgenden Berechnungen finden ausschließlich mit den eigens hierfür eingeführten schwarzen Sektoren statt.
Das Verschieben der Transparentpapierverläufe wird ersetzt durch numerisches Suchen von "ähnlichen" Sektoren.
Dabei wird in folgenden Schritten vorgegangen:
- Ähnlichkeitsmatrix aufstellen
- Häufigkeitsverteilung ermitteln
- gewichtete relative Wahrscheinlichkeiten errechnen
Am Ende steht der Sektor mit der höchsten Wahrscheinlichkeit als der gesuchte Vorrundensektor fest.
Doch der Reihe nach:
Was ist die Ähnlichkeitsmatrix?
Die Ähnlichkeitsmatrix beschreibt, ob sich zwei Sektoren ähnlich sind. "Ähnlich" bedeutet, dass sich die Sektordaten bis auf eine geringe Abweichung gleichen. ("Eine enge 50cm lange 90° Rechtskurve ist einer anderen 48cm langen engen 94° Rechtskurve ähnlich - aber nicht einer 130cm langen Geraden"). Aufgrund der reinen Zahlenvergleiche kann noch nicht sicher zwischen dem echten Vorrundensektor und einem an anderer Stelle liegenden ähnlichen Sektor unterschieden werden, was hier aber auch noch nicht der Fall sein muss. Hierfür kommt später dann die Gewichtung der so gefundenen Kandidaten ins Spiel.
Bei dieser Ähnlichkeitsbetrachtung wird jeder Sektor der Sektorenliste mit jedem anderen Sektor davor verglichen. Die Ergebnisse kann man sich als Matrix notiert vorstellen.
Die rechts gezeigte Ähnlichkeitsmatrix basiert auf nur sechs Sektoren pro Runde. Das wurde so gewählt, damit die Tabelle hier in der Darstellung noch handlich bleibt. Die Werte sind frei erfunden und dienen nur zur Verifikation des Algorithmus. Die tatsächlich gemessenen schwarzen Sektordaten sind deutlich reproduzierbarer. Die Zahlenreihe ist also ein Extrembeispiel für schlechte Sektordaten. Dennoch soll auch hiermit die Positionsbestimmung noch möglich sein. (Die Zahlenwerte sind: 353, 208, 400, 479, 627, 125, 358, 207, 186, 211, 479, 619, 481, 207, 186, 214, 477, 607, 482, 207, 185, 210, 477, 585, 453, 206; das Ähnlichkeitskriterium hier sei ausschließlich der reine Zahlenwert; Toleranz +-10).
Lesebeispiel: Der aktuelle Sektor (hier: 25) wird vergleichen mit allen seinen Vorgängersektoren (also von 0..24). Daraus entsteht dann die unterste Zeile (Zeile 25). Für jeden Sektor, der dem Sektor 25 ähnlich ist, wird ein Kreuz gesetzt. Genauso wird für alle anderen Sektoren/Zeilen verfahren. Nach rechts wird nicht die Vergleichssektornummer aufgetragen, sondern die Anzahl der Zeilen, die die beiden Sektoren in der Liste voneinander trennen (also der "Abstand" bzw. das Delta der Sektornummern). Das Kreuz bei Zeile25/Spalte4 (=Z25S4) bedeutet somit: Sektor 25 ist dem Sektor ähnlich, der einen Abstand/Delta von 4 zu ihm hat - also Sektor 21 (25-4=21). => "Sektor 25 und Sektor 21 sind sich ähnlich". Diese Darstellung hat ihren Vorteil darin, dass sich die Rundenlänge (in Sektoren) mit einem Blick ablesen lässt. In vielen Zeilen ist in Spalte 6 ein Kreuz => eine komplette Runde besteht wahrscheinlich aus 6 Sektoren.
Übrigens, uns interessiert ja eigentlich der Vorrundensektor. Wenn wir aber wissen wie groß die (momentane) Rundenlänge ist, dann können wir daraus natürlich auch den Vorrundensektor errechnen.
Häufigkeitsverteilung
Die Häufigkeitsverteilung erlaubt eine Aussage darüber, welches die wahrscheinlichste Rundenlänge ist. Sie ist die Summe aller Kreuze in einer Spalte. Für Spalte 6 ergibt sich somit eine Häufigkeit von 13. D.h. 13 der 25 Sektoren sind denen ähnlich, die in der Liste 6 Sektoren davor stehen. Die Häufigkeitsverteilung fließt in die Berechnung der gewichteten relativen Wahrscheinlichkeit ein.
Was hat es mit der gewichteten relativen Wahrscheinlichkeit auf sich?
Da die Ähnlichkeitsmatrix alle Sektoren liefert, die sich ähnlich sind, aber keine Bewertung/Gewichtung für den wahren Vorrundensektor einführen kann, muss diese Information über ein anderes Verfahren ermittelt werden.
Die für den Vorrundensektor relevante Zeile in der Ähnlichkeitsmatrix ist immer die letzte Zeile, also hier Zeile 25. Alle mit einem Kreuz versehenen Sektoren sind die Kandidaten, die für den Vorrundensektor in Frage kommen. Im Beispiel rechts sind das die Sektoren 21 (=25-4), 19 (=25-6), 13 (=25-12), 9 (=25-16), 7 (=25-18) und 1 (=25-24). Doch welcher davon ist der richtige? Die Frage lässt sich mit der "gewichteten relativen Wahrscheinlichkeit" beantworten. Diese lässt sich so bestimmen: Die Wahrscheinlichkeit, dass der jeweilige Kandidat dem gesuchte Vorrundensektor entspricht, verhält sich wie die Verteilung der Häufigkeit der Kandidaten (in der betrachteten Spalte) zur Gesamthäufigkeit. Oder anders gesagt: Wenn häufig ein Kreuz in der Spalte für Rundenlänge=6 ermittelt wurde, dann ist die Wahrscheinlichkeit hoch, dass die wahre Rundenlänge tatsächlich 6 beträgt ("Mehrheitsentscheid"). Deswegen wird die Rundenlänge=6 auch bei der Positionsbestimmung für den aktuellen Sektor durch die relative gewichtete Wahrscheinlichkeit bevorzugt (=> "höherer Prozentwert").
Der Prozentwert errechnet sich aus dem Wert der Häufigkeitsverteilung * 100% dividiert durch die Sektorhäufigkeitssumme. Die Sektorhäufigkeitssumme ist die Summe aller in dieser Zeile beteiligten Häufigkeiten. Für Zeile 25 wäre dies: 4+13+6+1+2+1 = 27. Für Zeile/Sektornr. 25 und Rundenlänge=4 (also für Vergleichssektornr. 21) erhält man 4*100/27 = 14%. Für eine Rundenlänge=6 ergibt sich ein Zahlenwert von 13*100/27 = 48%. Die restlichen Kandidaten haben eine relative gewichtete Wahrscheinlichkeit von 22%, 3%, 7%, 3%.
Hinweis: Die Matrix (rechts) ist komplett mit Wahrscheinlichkeitswerten ausgefüllt. Für die Bestimmung des Vorrundensektors würde es auch ausreichen, wenn nur die unterste Zeile berechnet/dargestellt wäre.
Der Kandidat mit der höchsten Wahrscheinlichkeit soll als Vorrundensektor anerkannt werden. In diesem Fall ist dies der Sektor 19 mit Rundenlänge/Delta=6. Ein Blick in die Liste der Zahlenwerte (im Text oben) ergibt: Sektor25 hat einen Zahlenwert von 206, Sektor19 hat einen Zahlenwert von 207 => passt.
Für manche Zeilen lassen sich überhaupt keine Kandidaten finden, d.h. es kann kein Vorrundensektor bestimmt werden. => Infolge darf das Auto nur mit verringerter Geschwindigkeit weiterfahren, bis die Position auf dem Streckenmodell erneut feststeht (=wieder ein Vorrundensektor ermittelt werden kann). Die nächste Gelegenheit hierzu bietet sich dann, wenn der nächste schwarze Sektor gemeldet wird.
Aber selbst wenn ein Kandidat mit einem hohen Prozentsatz (oder gar mit 100%) versehen ist, heißt dies nicht zwangsläufig, dass dies auch der wahre Vorrundensektor ist. Tatsächlich könnte es auch sein, dass dieser durch besondere Ereignisse (z.B. Räder drehen für längere Zeit durch) komplett "versteckt" ist und nicht mehr dem wahren Vorrundensektor ähnlich ist (evtl. aber jetzt zufällig einem anderen).
Aus den ermittelten Kandidaten deutet die relative gewichtete Wahrscheinlichkeit denjenigen heraus, der es mit der höchsten Wahrscheinlichkeit auch ist. (Nebenbei bemerkt: Bisher hat sich das Gcp praktisch noch nicht einmal verbremst und ist deswegen aus der Kurve geflogen, hat aber öfters keinen Kandidaten finden können und musste deswegen bis zum nächsten Syncpunkt langsam fahren).
Da die Rundenlänge hier ja nur 6 Sektoren beträgt, die Liste aber 26 Sektoren aufnehmen kann, müssten doch eigentlich mehrere Runden in der Liste auftauchen. Wieso synchronisiert sich der Algorithmus nicht versehentlich auf z.B. -12 Sektoren auf? Das könnte theoretisch durchaus passieren. In der Ähnlichkeitsmatrix sieht man auch in Spalte Delta=12, Delta=18 (schon weniger) und Delta=24 (nur sehr theoretisch) ebenfalls Ähnlichkeitshäufungen. Das Problem löst sich quasi von selbst, da die oberen Zeilen weniger Kreuze beitragen können (und wenn überhaupt, dann liegen diese wegen der Dreiecksform in den linken Spalten) und erfahren deswegen auch eine geringere Gewichtung.
Was passiert eigentlich in Zeile 9 oder Zeile 12? Hier vertut sich der Algorithmus komplett und wählt einen falschen Kandidaten. Würde das mit echten Messwerten passieren, dann könnte das Fahrzeug letztendlich von der Strecke fliegen.
Wieso beträgt in Zeile 10 und 11 die angebliche Rundenlänge = 7 Sektoren? Das liegt daran, dass in der Vorrunde (von Sektor 10 und 11), sich ein Sektor in zwei Sektoren aufgeteilt hat (z.B. durch Drift). Die Positionsbestimmung liefert also (auch) in diesem Fall einen korrekten Wert. Die Rundenlänge muss nicht für alle Ewigkeit konstant sein, sondern kann sich dynamisch zur Laufzeit ändern.
Was heißt eigentlich: Zwei Sektoren sind sich ähnlich?
Als Kriterien zur Ähnlichkeitsbestimmung dienen Sektorlänge, Sektorwinkel und Sektorlage. Die Begriffe Sektorlänge und Sektorwinkel sind aus obiger Beschreibung schon bekannt. Die Sektorlage ist die Ausrichtung des Sektors in der Ebene (z.B. der Sektor liegt im 270°-Winkel zur Start-Ziel-Geraden). Erst wenn alle Parameter mit ihrem Wert innerhalb eines erlaubten Toleranzbereiches sind, gelten zwei Sektoren als "ähnlich". Für die Sektorlänge haben sich 10 Wheelticks bewährt (das sind 10*17.5mm, also 17.5cm), der Sektorwinkel muss auf 5° identisch sein und die Lage darf um 60° abweichen. Das liegt im Langzeitdrift des Gyros begründet. Nach einer Drehung (z.B. nach einer Runde) liefert der Gyro nicht genau 360°, sondern weicht um bis zu 30° ab. Für Strecken die mehr als 360° Rundenwinkel haben (z.B. zwei ineinander verschachtelte Schleifen), muss die Lage folglich n*30° tolerieren (bei uns momentan auf 60° parametriert).
Fahrprofil: Jetzt steht der (schwarze) Vorrundensektor fest, was nun?
Der Vorrundensektor in der schwarzen Sektorliste liefert uns den Punkt, auf dem wir uns vor einer Runde befanden. Und da sich die Streckenführung definitionsgemäß nach genau einer Runde wiederholt, darf man ruhigen Gewissens davon ausgehen, dass der Vorrundensektor+1 derjenige Sektor ist, der als nächstes erreicht wird.
Doch die schwarzen Sektoren liefern nicht die Infos, die zur Berechnung von Bremspunkt und maximaler Kurvengeschwindigkeit notwendig sind. Ein Wechsel zur weißen Sektorliste ist erforderlich. Das Bindeglied zwischen den Listen sind die absoluten Wegpunkte. Wegpunkte sind die aufaddierten Wheelticks (Reflexkoppler-Pulse) und werden in jeder Fahrt kontinuierlich hochgezählt - sie wiederholen sich nie (vergleichbar mit dem Gesamtkilometerzähler im echten Auto). Da bekannt ist, an welchem Wegpunkt der schwarze Vorrundensektor lag, kann in der Liste der weißen Sektoren derjenige Sektor gesucht werden, in dessen Bereich ebenfalls dieser Wegpunkt fällt (muss ja nicht zwangsläufig auf eine weiße Sektorgrenze fallen). Jetzt ist der Abstand zur nächsten (weißen) Sektorgrenze bekannt und auch der charakteristische GyroZ-Wert (Bandmitte) des nächsten Sektors liegt vor.
Woher weiß das Fahrzeug mit welcher Geschwindigkeit ein bestimmter Kurvenradius gefahren werden kann?
Zunächst einmal hängt die maximale Kurvengeschwindigkeit eines Fahrzeugs von seiner Bodenhaftung (u.a. Magnet im Unterboden, Fahrbahnbelag, Gewichtsverteilung, Reifenart usw.) ab und muss für jedes Fahrzeug einmalig ermittelt werden. Bestimmt man diese Geschwindigkeit exemplarisch für einen oder zwei bestimmte Kurvenradien, so kann man dies auf andere Kurvenradien inter-/extrapolieren. Aus der Physik wissen wir, dass sich die maximale Kurvengeschwindigkeit bei doppeltem Kurvenradius um Faktor Wurzel2 erhöhen darf. (Zentripetalkraft Fz = m*v²/r). Diese Aussage wird durch praktische Beobachtungen gestärkt. Es lässt sich so ein Zusammenhang aufstellen, der in Abhängigkeit des GyroZ-Wertes (Betrag) eine maximal mögliche Drehzahl (=Geschwindigkeit) aufzeigt. Verpackt in einer (Lookup)Tabelle ergibt sich für unser Fahrzeug die rechts abgebildete Kennlinie. Der hyperbelförmige Verlauf wird durch einen unteren Wert begrenzt (hier z.B. 1400RPM). Dieser Wert steht für die Drehzahl, die auch am langsamsten Streckenabschnitt noch problemlos gefahren werden kann. Für Geraden (GyroZ=0) wurde eine Drehzahl von 8000RPM festgelegt. Diese wird mit unserem Fahrzeug auch bei sehr langen Geraden noch nicht erreicht. Übrigens, wenn von "Drehzahl" die Rede ist, ist damit immer die Drehzahl der Hinterachse gemeint. Die Motordrehzahl ist durch das Getriebe nochmals um den Faktor 3 höher.
Wann muss gebremst werden?
Aus der Momentangeschwindigkeit, und der im nächsten Sektor erlaubten Maximalgeschwindigkeit (ermittelt aus der Kennlinie) lässt sich der Bremsweg berechnen. Passt der Bremsweg gerade noch in den aktuellen Sektor hinein, dann wird's Zeit zu bremsen.
Das Bremsen wird dadurch erreicht, dass die Solldrehzahl langsam verringert wird (Bremsrampe). Eine sprungförmige Drehzahländerung würde zwar maximal stark verzögern, könnte aber in Kurven auch zu Instabilitäten des Fahrzeugs führen. Wenn sich z.B. eine schnelle Kurve "plötzlich" zuzieht, dann könnte das Fahrzeug beim abrupten Bremsen ausbrechen. Umgekehrt wird auch nicht sprungförmig beschleunigt, um keine durchdrehenden Räder zu provozieren (kein Magnet im Fahrzeugunterboden verbaut => wenig Bodenhaftung => Vollgas => durchdrehende Räder). Legt man die maximal (gewünschte) Verzögerung, als auch die maximal (gewünschte) Beschleunigung als Einstellparameter aus, so lässt sich der Algorithmus an Fahrzeug und Strecke anpassen. Es wäre auch denkbar, dass diese Parameter in einer Kalibrierfahrt automatisch von der Software ermittelt werden.
Muss überhaupt gebremst werden?
Liefert die Bremswegberechnung quasi einen negativen Bremsweg, d.h. die Drehzahl muss an der Sektorgrenze nicht verringert werden, dann muss geprüft werden, ob nicht sogar beschleunigt werden darf. Beschleunigt werden darf immer dann, wenn die Maximalgeschwindigkeit für den aktuellen Sektor noch nicht erreicht ist. Vor der Sektorgrenze darf noch nicht beschleunigt werden (also nicht wie im echten Auto bereits im Kurvenscheitel), da ja die Carrera Schienenteile einen konstanten Radius haben und somit in der ganzen Kurven nur eine (optimale) Geschwindigkeit erlauben. Ein früheres Beschleunigen würde zu übermäßigem Drift führen und letztendlich zu langsamerer Rundenzeit. Nebenbei bemerkt: Für frei gefräste Holzbahnen würde eine zulaufende Kurve durch die Sektorerkennung schon in mehrere Abschnitte aufgeteilt werden und diese Besonderheit würde sich dort nicht ergeben.
Drehzahlregler
Die von der Sollgeschwindigkeitsberechnung ermittelte Solldrehzahl ("SollRPM") wird an den Drehzahlregler übergeben, der daraus ermittelt, mit welchen PWM-Tastverhältnissen die Motortreiber-Mosfets angesteuert werden müssen. Es gibt einen Kanal zur Ansteuerung des "Fahr-Mosfets", der die Schienenspannung auf den Motor schaltet und einen Kanal für den "Brems-Mosfet" zum aktiven Bremsen, der den Motor kurzschließt. Beide dürfen natürlich nicht gleichzeitig angesteuert werden, da es sonst zu einem harten Kurzschluss kommt.
Der Regler ist als PI-Regler ausgelegt. Die Reglerparameter wurden experimentell so ermittelt, dass eine möglichst schnelle Annäherung an die Führungsgröße (SollRpm) gegeben ist, ohne dass der Regler (stark) überschwingt.
Die PWM-Kanäle werden mit 25kHz betrieben und lösen das Tastverhältnis in 0.1%-Schritten auf.
Elektronik
Als Spenderfahrzeug für das Gcp musste ein ausrangiertes Carreraauto herhalten, dessen Elektronik durch eine eigene Platine ersetzt wurde. Neben den Sensoreingängen und den Motortreibern erwies sich auf dem Prototypen auch eine Kommunikationsschnittstelle zum PC für Logging/Debug-Aufgaben als zwingend notwendig.
|
Technische Daten:
|
Der Gyrosensor liefert einen Drehratenwert (skaliert in 70 MilliDegrees per Second; mdps) und wird zyklisch jede 1ms ausgelesen.
Zur Drehzahlmessung (und Entfernungsmessung) wurde auf der hinteren Antriebsachse eine Scheibe angebracht, die pro Radumdrehung 8 Flankenwechsel liefert. Da wir momentan nur die High-Low-Flanken auswerten erhalten wir bei einem Radumfang von 70mm eine Auflösung von 17.5mm pro Reflexkoppler-Impuls. Der Impuls wird nicht nur gezählt, sondern der genaue Zeitpunkt wird zusätzlich per InputCapture-Einheit erfasst, um eine deutlich höhere zeitliche Auflösung zu erhalten und somit die Raddrehzahl auch bei "niedrigen" Drehzahlen sauber erfassen zu können. Im relevanten Drehzahlbereich von ca. 1000RPM..8000RPM kommt im Schnitt etwa alle 1..10ms ein Wheeltick (=17.5mm).
Die beiden Beschleunigungs- und Bremsmosfets werden mit einem Mosfet-Treiber angesteuert, da diese weniger Platz auf der sowieso knappen Platinenfläche einnimmt und auch die Dimensionierung der sonst notwendigen diskreten Mosfet-Beschaltung vereinfacht.
Der verwendete HCS12-Prozessor von Freescale wurde gewählt, weil dieser aus anderen Projekten bereits vertraut war und die technischen Daten (Taktfrequenz, Speicher) dem Einsatz nicht im Wege standen, bzw. alles so ausgelegt wurde, dass die Ressourcen passen.
Versuche mit 3-Achsen-Beschleunigungssensoren brachten keine befriedigenden Ergebnisse, weshalb diese (auch aus Platzgründen) nicht verbaut wurden. Das Nutzsignal war in der gleichen Größenordnung wie das Rauschen, woraus sich keine sinnvoll verwertbaren Daten ableiten ließen. Ursache dafür waren vermutlich die starken Motor- und Fahrbahnvibrationen, die sich trotz mechanischer Entkopplung (Moosgummi) nicht ausreichend verbesserten.
Der Leitkielwinkelsensor wurde als Vorhalt eingeplant, um den fahrdynamischen Grenzbereich (wenn das Fahrzeug langsam in den Drift übergeht) besser ausmessen zu können. Der Leitkiel ist eine Führungsschiene im Unterboden des Fahrzeugs, die im Schlitz in der Fahrbahn entlangläuft und zur Spurführung dient. Hierzu wird die Leitkielstellung relativ zum Fahrzeug gemessen. Bei Kurveneinfahrten dreht sich der Leitkiel relativ zum Fahrzeug ein Stück zur Seite. Übersteigt dieser Winkel einen bestimmten Wert, so kann man daran ein Driften des Fahrzeugs ablesen. Durch Montage eines kleinen Magneten auf dem Leitkiel lässt sich dessen Winkel bzw. Verdrehung relativ zum feststehenden MagnetWinkelencoder messen. Der magnetische Winkelauflösung beträgt 12Bit, was ca. 0.1° entspricht - also weit genauer als hier nötig wäre. Alle 4ms wird ein neuer Messwert geliefert. Derzeit messen wir den Leitkielwinkel zwar, verwerten die Daten aber nicht. Grund: Da die Montage relativ aufwendig ist (modifizierter Leitkiel; Befestigungsmöglichkeiten), wollten wir nur dann auf die Daten zurückgreifen, falls eine ausreichend schnelle Fahrt nicht ohne diesen möglich wäre.
Das Einlesen der Carrera Digitaldaten auf den Schienen ist dazu gedacht, um das Fahrzeug vom Benutzer parametrieren und manuell fahren zu können. Denkbar wäre es z.B. die Fahrgeschwindigkeit künstlich einzuschränken oder den Fahrbeginn vom Benutzer per Handregler starten zu können. Voraussetzung dafür ist ein schnelles und ungepuffertes Einlesen der Schienenspannung. Die Schiene führt bei Digitalbahnen auf der einen Spur Gnd und auf der Anderen einen Pegel von 12-18V je nach Trafo. Zur Kommunikation von der Carrera-Steuereinheit zum Fahrzeug ist der Gleichspannung ein PWM-Signal überlagert. Eine Datenübertragung vom Fahrzeug zur Steuereinheit ist nicht vorgesehen. Das ungepufferte Einlesen der Schienenspannung steht in entgegengesetzter Anforderung zu einer stabilen Spannungsversorgung für die Elektronik. Durch Lücken in der Schiene ("Weichen") kommt es zu Aussetzern von ein paar wenigen Zentimetern bzw. wenigen hundert Millisekunden, die von einem Stützelko überbrückt werden müssen. Die überlagerten Kommunikationssignale sind deshalb (per Diode) von der internen Versorgung entkoppelt.
Grundsätzlich unterstützt das GCP auch Analogbahnen mit einer konstanten Spannungsversorgung (=> "Handregler per Klebeband auf Vollgas fixieren")
Die IR-Sendediode im Fahrzeugboden erlaubt bewusst eingeleitete Spurwechsel, um z.B. jederzeit auf der Ideallinie fahren zu können. Um die anderen Fahrzeug nicht abzuschießen, würde das aber praktisch auch mehr Rundumsicht benötigen (=> "Abstandssensoren"). Automatische Spurwechsel sind derzeit aber noch nicht implementiert.
Um den Reflexkoppler einzusparen, und so den Nachbau zu erleichtern, bzw. zu verbilligen, haben wir auch die Drehzahl ohne Reflexkoppler getestet ("Drehzahlmessung per Gegen-EMK"). Dabei wird ausgenutzt, dass die im Motor induzierte Gegenspannung proportional zu seiner Drehzahl ansteigt. Misst man diese "elektromotorische Kraft" zu einem Zeitpunkt in der der Motor nicht bestromt wird ("PWM-Aus"-Phase), so kann man eine Aussage über seine Drehzahl treffen. Praktisch funktioniert dies auch prinzipiell, allerdings war die Messung nicht so genau wie die Drehzahlmessung per Reflexkoppler, was dann den Regler (bzw. unsere Reglerparameter) überforderte. Das Fahrzeug fuhr deutlich "unrunder". Das Motorgeräusch war schrecklich. Deshalb haben wir diese Option bisher auch noch nicht weiter vertieft, obwohl da noch Verbesserungspotential stecken dürfte.
Software
Neben den obligatorischen Komponenten wie Scheduler und Lowlevel-Treibern (InputCapture, Pwm, Adc, Spi) besteht der Kern der Gcp-Software aus den beiden Komponenten Kommunikationsmodul (ApplComm) und allem, was mit der Bestimmung Fahrzeugposition und Ansteuerung des Motors zusammenhängt (ApplLap).
ApplLap: Sektorerkennung, Positionsbestimmung und SollDrehzahlberechnung
Die oben beschriebenen Konzepte und Ideen sind im Modul ApplLap (Download) implementiert. Der zentrale 1ms-Task, in dem alle zyklisch anfallenden Arbeiten ausgeführt werden, verwaltet die einzelnen Teilkomponenten, wie Sektorerkennung weiß, Sektorerkennung schwarz und SollDrehzahlberechnung. Die Teilkomponente Positionsbestimmung ist weniger zeitkritisch, aber relativ rechenzeitintensiv, weshalb diese nicht wiederkehrend alle 1ms gerechnet wird, sondern nur dann, wenn ein neuer potentieller Syncpunkt anfällt (also ein neuer schwarzer Sektor geliefert wird). Die Ausführung findet im IdleTask statt, der immer dann (weiter)gerechnet wird, wenn der 1ms-Task seine Arbeit erledigt hat. Die Positionsbestimmung wird somit ständig von den zyklischen 1ms-Aufgaben unterbrochen. Es ist mit dem aktuellen Stand der Software so, dass der 1ms-Task maximal 820µs Laufzeit verbraucht und für den Idletask pro 1ms nur (minimal) 180µs Rechenzeit übrig bleiben. Letztendlich liefert die Positionsbestimmung dann aber nach spätestens 30ms einen neuen Syncpunkt. (Der zwischenzeitlich verfahrene Weg wird natürlich berücksichtigt).
ApplComm: Kommunikation zum PC
Das Kommunikationsmodul (Download) implementiert ein kleines Protokoll zur Datenübertragung zum PC. Hierüber werden in verschiedenen Modi (die vom PC vorgegeben werden) folgende Daten vom Fahrzeug an den PC gesendet:
- LiveMeasure-Daten: interne Variablen zur (grafischen) Echtzeitanalyse, wie z.B. MomentanDrehzahl, SollDrehzahl, aktueller GyroZ-Wert, Debugvariablen usw.; bis zu 6 Parameter werden (typ.) alle 50ms übertragen.
- Fastlog: Echtzeitübertragung aller physikalischen Eingangsgrößen(!)
- weiße und schwarze Sektordaten: Länge, Wegpunkt, Winkel, Lage, Bandmitte zur späteren automatischen oder händischen Auswertung.
- SyncTelegramme: Wegpunkt der Synchronisierung und um wie viele Wheelticks ("cm") die errechnete Position korrigiert werden musste
- Diagnosedaten, wie z.B. Prozessorauslastung im 1ms-Task/Idle-Task, um Ressourcenprobleme erkennen zu können.
PC-Software zur Auswertung und Simulation
Die empfangenen LiveMeasure-Daten werden von einer dafür entwickelten PC-Software in Echtzeit in einen Graphen eingetragen und helfen somit bei der visuellen Bewertung der Fahrzeugsituation. Hilfreich ist dies z.B. beim Aufspüren von Fahrzeugdrifts am Kurveneingang oder -ausgang (GyroZ-Sprung/Schwinger im Graphen) oder bei der Bewertung der Reglerparameter ("Istdrehzahl schwingt über"). Da hierbei nicht alle Messwerte übertragen werden können, reicht diese Analysemethode nur für erste grobe Einschätzungen.
Daneben gibt es aber viele Situationen, die schwieriger zu bewerten sind. Zum einen, weil nicht alle, zur Analyse nötigen Daten, vorliegen (50ms Aktualisierungsrate reicht oft nicht aus), zum anderen, weil die 6 Livemeasure-Kanäle nicht ausreichen.
Die Frage "Wieso wurde die Sektorgrenze nicht gesehen" lässt sich nicht nur durch Betrachten des GyroZ-Verlaufes beantworten, sondern es ist notwendig den Algorithmus live zu beobachten. Da sich das Fahrzeug aber bewegt und sich damit eine Onboard-Debugmöglichkeit ausschließt, mussten die Daten zur späteren Auswertung aufgezeichnet werden. Hierzu nimmt der PC die in Echtzeit / live gesendeten physikalischen Messgrößen entgegen (Betriebsart "Fastlog" und liegt diese in einem Logfile ab. Dadurch können auch sehr lange Messfahrten problemlos aufgezeichnet werden. Am Ende werden die physikalischen Eingangsgrößen am PC genauso nachgerechnet, wie diese auch im Fahrzeug berechnet wurden. So ist es möglich zu beliebigen Zeitpunkten und an beliebigen Stellen das Verhalten des Algorithmus zu betrachten/debuggen und die grafische Ausgabe zu analysieren. Die PC-Software enthält hierzu eine Komponente (Targetcode.cs), in dem der (relevante) Microcontrollercode fast 1:1 identisch nachgerechnet wird. Die Dateien lassen sich relativ einfach per Diff-Tool auf gleichem Stand halten.
Um algorithmische Probleme zu lösen, die keinen Echtzeitbezug benötigen, reichen die Daten der Sektortelegramme aus. Für die heuristische Positionsbestimmung z.B. ist eine Simulation umgesetzt, die als Eingangsdaten, rein die gelieferten Sektordaten benötigt. In der Ausgabe der Simulation lassen sich somit einfach die Ähnlichkeitsmatrix, Häufigkeitsverteilung oder gewichtete relative Wahrscheinlichkeit realer Fahrzeugsituationen analysieren.
Auch das Bestimmen der Parameter für die Sektorerkennung (weißer Algorithmus) ließ sich sehr anschaulich über eine PC-Simulation lösen. Hier kann in Echtzeit grafisch beobachtet werden, welchen Einfluss das Verstellen der Parameter auf die Wahl der Sektorgrenzen hat (siehe Video). So ist schnell überprüfbar, ob die Sektordaten sinnvoll die tatsächliche Kurvenform (GyroZ-Verlauf) wiedergeben können.
Fazit: Ohne die umfangreichen Simulationsmöglichkeiten wäre es unmöglich gewesen auch nur ansatzweise ein autonom fahrendes Fahrzeug zu bauen. Der Einsatz des Prozessordebuggers konnte auf die Fälle beschränkt werden, an denen (einfache) elektrische/physikalische Probleme auftaten (z.B. Probleme beim Einlesen der Reflexkoppler-Daten aufgrund von Prellen, bzw. der elektrische Signalform und bei Implementationsfehlern im Kommunikationsprotokoll...). Die restlichen, schwierigeren algorithmischen Implementationsprobleme ließen sich komfortabel in der Simulation austesten.
Probleme bei Planung und Durchführung
Schneller als erwartet und ohne ernste Probleme ging die Entwicklung der Hardware inkl. Grundsoftware vonstatten. Schon nach wenigen Wochen(enden) hatten wir ein erstes fahrfähiges Muster in der Hand. Da dieses bereits dank Drehzahlerfassung mit konstanter Drehzahl fahren konnte und nicht mit konstanter PWM fahren musste (das führt in Kurven dazu, dass die Geschwindigkeit aufgrund erhöhter Reibung minimal einbricht), war das GCP bereits geringfügig schneller als das originale Carrera Ghostcar. Eigentlich war unser erstes Projektziel damit schon erreicht.
Danach ging es an die Erfassung des Streckenmodells ("weißer Algorithmus"). Wir konnten ohne PC-Simulation und ohne Livedatenerfassung aus dem Fahrzeug nicht zu brauchbaren Parametern für den weißen Algorithmus gelangen. Also musste eine umfangreiche Log-/Debug-Infrastruktur aufgebaut werden. Die Ideen zur Verbesserung der weißen Sektordaten bzw. "Erfindung" des schwarzen Algorithmus ließen etwas auf sich warten, waren aber einige Wochen und (Matlab)Simulationen später, umsetzungsreif und implementierbar. Das größte und am meisten unterschätzte Problem war jedoch die eigentliche Positionsbestimmung. Nachdem bereits gute und reproduzierbare Sektordaten vorlagen, waren wir zunächst guter Dinge, dass dies nur noch ein kleiner Schritt sein müsste. Wir waren bis dahin davon ausgegangen, dass wir mit einer Referenzfahrt zur Aufzeichnung der Sektordaten beginnen könnten, die dann in die Ghostcarfahrt übergehen würde. Wir konnten keine Kriterien finden, die sauber bei jedem denkbaren Streckenverlauf ein Rundenende erkennen konnte. (Theoretisch kann man dies wohl beweisen/erkennen, wenn man bereits zwei(!) vollständige Runden zurückgelegt hat - praktisch ist uns das algorithmisch aber nicht zuverlässig gelungen).
Letztendlich vergingen ungefähr 8 Monate bis das Konzept der Positionsbestimmung in der jetzigen Form feststand. Damit waren alle Voraussetzungen für eine autonome Fahrt geschaffen. Es war ein spannender Augenblick, als das Auto zum ersten Mal auf Geraden beschleunigte und vor Kurven rechtzeitig bremste. (Siehe Video) Eigentlich wollten wir vorher noch das Fahrzeug gegen Einschläge polstern, was dann aber doch irgendwie vergessen wurde...
Auch wenn zum aktuellen Projektstand das Gcp noch keine Konkurrenz für einen trainierten Fahrer ist, so fährt es Anfängern doch davon. Es ist also noch Potential nach oben vorhanden, vor allem, wenn man Drifts zur Verbesserung der Rundenzeit zulässt. Sofern man überhaupt davon ausgeht, dass damit die Rundenzeit tatsächlich schneller wird - was noch zu beweisen wäre...
Verbesserungsideen
- Alles was die Rundenzeit verbessert
- Auswertung des Leitkielwinkels zur Erkennung von fahrdynamischen Grenzbereichen; "Kontrolliertes driften"
- Durch Überschwinger am Kurvenende bei höherer Geschwindigkeit werden zusätzliche schwarze Sektoren erzeugt, die bei langsamerer Fahrt nicht auftreten und deswegen zu Syncproblemen führen. Diese zusätzlichen Sektoren könnten ausgeblendet/unterdrückt werden (Modifikation Schwarzer Algorithmus) und somit eine höhere Grundgeschwindigkeit gefahren werden. (Derzeit fahren wir noch nicht an der physikalischen Haftgrenze, sondern an der "Reproduzierbarkeitsgrenze" der schwarzen Sektoren).
- Alles was die Fahrt besser macht
- Beschleunigen nicht nach Streckenmodell, sondern nur nach aktuellem GyroZ. Dadurch wird der Beschleunigungspunkt nicht "verpasst" und auch nicht zu früh begonnen zu beschleunigen.
- Dynamische Bandhöhe: Eine höhere Auflösung der gewählten Bandhöhe bei kleinen GyroZ-Werten würde zu weniger gemeldeten weißen Sektoren führen und damit weniger Speicherplatz bzw. Listenplätze belegen. Würden die angelegten Bänder um den GyroZ-Wert nur im Bereich um GyroZ -1000..+1000 hoch aufgelöst werden, weil genau in diesem Bereich hohe Geschwindigkeiten gefahren werden (können), so müsste man die Momentangeschwindigkeit nicht vom (betragsmäßig) größten GyroZ-Wert in diesem (hohen) Band abhängig machen => ebenfalls schnellere Fahrt möglich.
- Die Bremspunktbestimmung schaut momentan zwei Sektoren in die Zukunft. Würden zwei sehr kurze, aber schnelle Sektoren anstehen, aber ein dritter sehr enger Sektor folgen, könnte dieser übersehen werden und das Bremsen zu spät eingeleitet werden. (Unklar, ob eine solche Strecke mit Carreraschienen praktisch überhaupt gebaut werden kann).
- "GapSektoren": Als weiteres Kriterium für die Positionsbestimmung könnte die Lage der "Schienenlücken" (Unterbrechungen der Stromleiter durch Weichen, Kreuzungen) dienen. Erkennung durch Schienenspannungsmessung; Vorteil: ortsfest; Nachteil: Nicht auf allen Bahnen vorhanden; Ausgiebige Tests zeigten sehr gute Eignung
- Alles was das Fahren interessanter machen könnte
- Abstandssensoren, um Spurwechsel überhaupt erst zur ermöglichen (kein Abschießen von nebeneinander fahrenden Autos) und um dicht vor oder hinter einem anderen Fahrzeug fahren zu können.
- Einstellbare Geschwindigkeit des Ghostcars, um sich auf verschieden starke Gegner abstimmen zu können
- Tuningparameter vom Benutzer einstellbar machen. Dadurch könnte dieser sein Fahrzeug auf seine Strecke abstimmen. Dies könnten z.B. folgende Parameter sein:
- maximale Beschleunigung (bessere Reifen, besserer Grip => höhere Beschleunigung möglich). Eine zu hoch eingestellte Beschleunigung würde zu durchdrehenden Rädern führen und somit Rundenzeit kosten.
- Variation des ermittelten Bremspunkts: Wie knapp soll wirklich gebremst werden (Sicherheitsreserve vs. Risiko)
- Kennlinie; Abhängigkeit der Geschwindigkeit vom Kurvenradius (hohes Optimierungspotential; stark Strecken- und Fahrzeugabhängig)
- Ausnutzung der Weichen, um Wegstrecke zu sparen
- und noch viele weitere Ideen...
Sonstiges
Aufgrund des begrenzten Umfangs dieses Artikels, müssen leider viele Punkte offen bleiben oder werden nur in einem kurzen Nebensatz angerissen. Sollten noch Fragen auftauchen, bitte melden.
GCP ist ein Freizeitprojekt von and_ref und galoscha. Eine kommerzielle Verwertung ist nicht gestattet. Bei entsprechendem Interesse bitte anfragen. :-)
Kontakt: André; and_ref (at) canathome.de