Logische Verknüpfungen

Inhaltsverzeichnis

1 UND
2 ODER
3 NICHT
4 NAND
5 NOR
6 XOR
7 XNOR

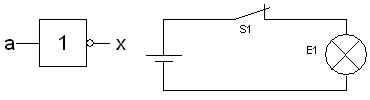
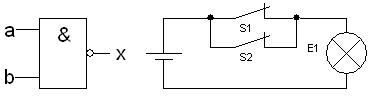
[Bearbeiten] UND

(Konjunktion)

$x = a \wedge b$

a	b	x
0	0	0
0	1	0
1	0	0
1	1	1

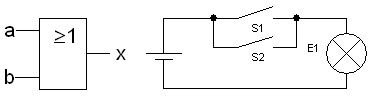
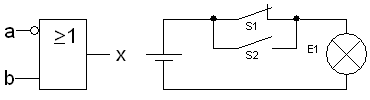
[Bearbeiten] ODER

Verknüpfung (Disjunktion)

$x = a \vee b$

a	b	x
0	0	0
0	1	1
1	0	1
1	1	1

[Bearbeiten] NICHT

Verknüpfung (Negation)

$x = \overline{a}$

a	x
0	1
1	0

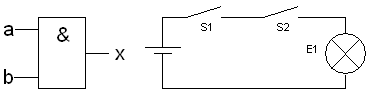
[Bearbeiten] NAND

Verknüpfung

$x = \overline{a \wedge b}$

a	b	x
0	0	1
0	1	1
1	0	1
1	1	0

[Bearbeiten] NOR

Verknüpfung (Konjunktion)

$x = \overline{a \vee b}$

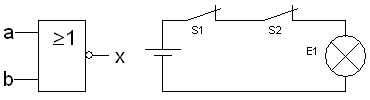a	b	x
0	0	1
0	1	0
1	0	0
1	1	0

[Bearbeiten] XOR

Exklusiv-ODER-Verknüpfung (Antivalenz)

$x = (a \wedge \overline{b}) \vee (\overline{a} \wedge b)$

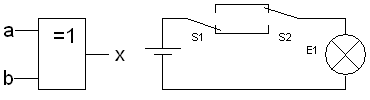a	b	x
0	0	0
0	1	1
1	0	1
1	1	0

[Bearbeiten] XNOR

Exklusiv-NOR-Verknüpfung (Äquivalenz)

$x = (a \wedge b) \vee (\overline{a} \wedge \overline{b})$

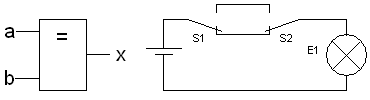a	b	x
0	0	1
0	1	0
1	0	0
1	1	1

Sperrgatter (Inhibition)

$x = \overline{a} \wedge b$

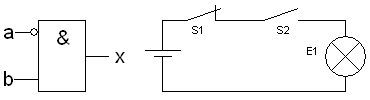a	b	x
0	0	0
0	1	1
1	0	0
1	1	0

Subjunktion (Implikation)

$x = \overline{a} \vee b$

a	b	x
0	0	1
0	1	1
1	0	0
1	1	1

www.mikrocontroller.net

▶ Dieser Artikel

▶ Benutzer

▶ Suche

▶ Werkzeuge