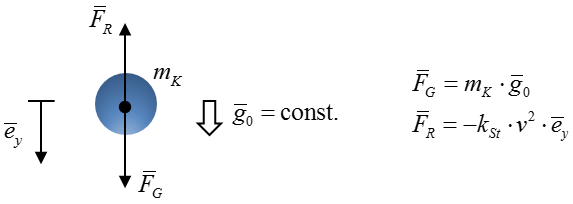Multi-Domäne-Systeme
von Joe G.
(Artikel noch in Bearbeitung)
Multi-Domäne-Systeme beschreiben komplexe Systeme, deren Einzelkomponenten aus verschiedenen Bereichen der Technik (Elektrotechnik, Mechanik, Pneumatik, Hydraulik oder Thermodynamik) stammen.
Mit Hilfe der Multi-Domain-Modellierung können diese Systeme mittels moderner Simulationsmethoden (LTSpice) analysiert und berechnet werden. Das theoretische Gerüst wird in diesem Artikel ausdrücklich nicht behandelt. Vielmehr erfolgt hier eine Darstellung im Sinne eines „Kochrezeptes“ um den interessierten Praktiker an die Methoden der Multi-Domain-Modellierung heranzuführen. Über die praktische Anwendung hinaus interessierte Leser, nutzen bitte die jeweils angegeben Quellen zur Vertiefung.
Grundlagen
Mehrpolbasierte Modellbildung
Als mehrpolbasierte Modellbildung bezeichnet man eine einheitliche Darstellung von technischen Systemen mit multidisziplinärem Charakter (Multi-Domänen-Systeme). Ausgehend von der Modellbildung mit konzentrierten Ersatzelementen, sowie allgemeiner Erhaltungs- und Bilanzgesetze, können Systemmodelle mit leistungserhaltenden Verschaltungsgesetzen gebildet werden ([1]elektroanaloge Netzwerke, [2]Verallgemeinerte Netzwerke in der Mechatronik). Ein klassisches Beispiel für reine elektrische Systeme sind die kirchhoffschen Netzwerke. Historisch geht diese Form der Modellbildung auf James Clerk Maxwell zurück. Er entwickelte 1873 sehr detaillierte mechanische Analogien zu den elektrischen Phänomenen. In seiner [3]Impedanzanalogie verknüpfte er erstmals die Kraft und die elektrische Spannung als analoge Größen.
Allgemeines
Bei der mehrpolbasierten Modellbildung werden konzentrierte Netzwerkelemente (engl. lumped elements) über ihre Torklemmen miteinander verschaltet. Dabei findet ein wechselseitiger Energieaustausch zwischen den einzelnen Netzwerkelementen statt. Abhängig von der Anzahl der vorhandenen Torklemmen jedes Netzwerkelements spricht man von einem Eintor, Zweitor, Dreitor oder Mehrtor. Der Energieaustausch eines Netzwerkelementes kann immer durch die zwei elementare Netzwerkvariablen (Torgrößen), der Flussgröße IX und der Differenzgröße Y beschrieben werden. Die Verschaltung der einzelnen Netzwerkelemente untereinander erfolgt mittels verallgemeinerter Kirchhoffscher Gesetzte (Kontenpunktsatz, Maschensatz).
Bildungsgesetze für die Systemvariablen
Bei der Bildung aller notwendigen Systemvariablen geht man zunächst davon aus, dass eine Energieänderung im n-dimensionalen Raum immer durch eine Massieu-Gibbs-Funktion ausgedrückt werden kann.
Innerhalb einer physikalischen Domäne existieren im Normalfall genau zwei Summanden der Massieu-Gibbs-Funktion, welche im Allgemeinen durch ihre unvollständigen Differentiale beschreiben werden.
Innerhalb einer physikalischen Domäne existieren im Normalfall genau zwei Summanden der Massieu-Gibbs-Funktion, welche im Allgemeinen durch ihre unvollständigen Differentiale beschrieben werden.
Die beiden Intensitätsgrößen bilden dabei die gesuchten Fluss- und Differenzgrößen (leistungskonjugierte Variablen).
Das Produkt beider Intensitätsgrößen ergibt in der jeweiligen physikalischen Domäne immer eine Leistung.
Jede einzelne unabhängige Energieänderung δE wird durch ein Paar von energiekonjugierten Variablen ausgedrückt.
Der Quantitätsbegriff reicht jedoch noch nicht aus, um alle Energieformen eindeutig zu charakterisieren. Bei Energieformen an denen feldartige Größen beteiligt sind, existiert kein einfacher mengenartiger Zusammenhang. Dazu wird der Begriff der Quantitätsgröße mit den nachfolgenden Regeln auf den Begriff der extensiven Größe erweitert.
Bildungsregel
- Zu jeder Energieform existiert eine extensive Variable.
- Jede Quantitätsgröße ist auch extensiv.
- Nicht jede extensive Größe ist eine Quantitätsgröße.
| Variable | Eigenschaft | Name | Formelzeichen |
|---|---|---|---|
| qP,qT | sind extensive Variablen | ||
| qP | ist eine Quantitätsgröße | Primärgröße | X |
| qT | ist keine Quantitätsgröße | Extensum | Ex |
Quantitäts- und Intensitätsgrößen
Innerhalb einer physikalischen Domäne lassen sich immer genau vier Systemvariablen bilden, zwei Quantitätsgrößen und zwei Intensitätsgrößen. Ausgehend von der Primärgröße können die drei restlichen Systemvariablen eindeutig mathematisch abgeleitet werden.
Ihre messtechnische Eigenschaft wird dabei durch ihren jeweiligen Index charakterisiert.
P – für durch (von lat. per, engl. through)
T – für über (von lat. trans, engl. across)
| Schritt | Systemvariable | Formelzeichen | Gleichung | Eigenschaft | Ernergievariable | Variable |
|---|---|---|---|---|---|---|
| 1 | Primärgröße | X | - | P-Quantität | qP | |
| 2 | Differenzgröße | Y | T-Intensität | iT | Y | |
| 3 | Flussgröße | IX | P-Intensität | iP | IX | |
| 4 | Extensum | Ex | T-Quantität | qT |
Übersicht über den mathematischen Zusammenhang der Systemvariablen
Beispiele
Die zugegeben doch etwas theoretische Abhandlung lässt sich anhand einer Beispiele sehr einfach nachvollziehen.
Beispiel 1: Mechanik Translationsbewegung
| Schritt | Systemvariable | Mechanik | Zusammenhang | Energie | ||
|---|---|---|---|---|---|---|
| 1 | Primärgröße | X | Impuls | p | ||
| 2 | Differenzgröße | Y | Geschwindigkeit | v | ||
| 3 | Flussgröße | IX | Kraft | F | ||
| 4 | Extensum | Ex | Weg | s |
Anmerkungen
- Energie, welche auf mechanischem Wege erzeugt wird, wird auch als Arbeit bezeichnet.
- Integriert man nach dp, so erhält man die bekannte Form der kinetischen Energie. WP=(m/2)v2
Beispiel 2: Elektrotechnik
| Schritt | Systemvariable | Elektrotechnik | Zusammenhang | Energie | ||
|---|---|---|---|---|---|---|
| 1 | Primärgröße | X | el. Ladung | Qel | ||
| 2 | Differenzgröße | Y | el. Spannung | Uel | ||
| 3 | Flussgröße | IX | el. Strom | Iel | ||
| 4 | Extensum | Ex | mag. Fluss | Φel |
Anmerkungen
- Schritt 2 entspricht dem Induktionsgesetz bzw. die Energie in einer Induktivität.
- Schritt 3 berechnet die Energie im Kondensator.
Konstitutiven Gesetze
Die konstitutiven Gesetze verknüpfen die vier Systemvariablen jeweils wechselseitig miteinander. Dabei ergeben sich zwei Gleichungen, welche den Vorgang der Energiespeicherung beschreiben und zwei Gleichungen, welche den Vorgang der Energiedissipation beschreiben. Geht man von der Modellvorstellung der idealen konzentrierten Ersatzelemente aus, so lassen sich die vier konstitutiven Gleichungen jeweils einem einzigen Bauelement zuordnen. Für rein lineare Bauelementebeziehungen ergibt sich der folgende Zusammenhang:
Für nichtlineare Kopplungen der Systemvariablen schreiben wir den entsprechenden Differentialquotienten. Im Allgemeinen wird der Differentialquotient aus einer Quantitätsgröße und einer Intensitätsgröße Suszeptibilität genannt. Kapazitäten und Induktivitäten sind im übergeordneten Sinne Suszeptibilitäten.
Bedeutung des Memristors
Der Memristor ist formal als Quotient der beiden Quantitätsgrößen Extensum und Primärgröße definiert. Um die physikalische Bedeutung des Memristors zu verstehen, rufen wir uns nochmals die Bildungsgesetze in Erinnerung. Die Wahl der Primärgröße X bestimmt vollständig alle weiteren Größen einer Domäne. Um innerhalb dieser Domäne alle Basisgrößen zu finden, ist es also nur notwendig, die Primärgröße und die jeweiligen Energien zu kennen. Potentialdifferenz, Mengenstrom und Extensum können über ihre festen mathematischen Ableitungen eindeutig gebildet werden. Somit sind zwei der vier Basisgrößen ausreichend, um auch eindeutig alle Netzwerkbauelemente (zwei Speichergrößen, eine dissipative Größe) zu bestimmen.
Historisch (nicht nur aus messtechnischen Gründen) haben sich dabei die beiden Intensitätsgrößen
IX und Y etabliert. Werden nur diese beiden Variablen in der Netzwerkdarstellung verwendet, so sind ihre Speicherelemente integrale Größen.
Oft sind jedoch ausschließlich lineare algebraische Beziehungen für weitere Berechnungen vorteilhafter. In diesem Fall sind die beiden Variablen Ex und X für die Darstellung der Speicherelemente günstiger.
Wie wir erkennen, sind die beiden Gleichungen für die Speichergröße gerade die Definitionsgleichungen dieser Speichergrößen. Zusätzlich wird aus dem Widerstand der Memristor. Da dieser für den linearen Fall jedoch mit dem Widerstand äquivalent ist, hat das Widerstandsäquivalent Memristor bisher keine große Verbreitung gefunden. Der Vollständigkeit halber gehört der Memristor jedoch zur Energieflussdarstellung.
Zusammenfassung
Die Ableitung der vier Systemvariablen innerhalb einer physikalischen Domäne erfolgt anhand einer einheitlichen Bildungsvorschrift. Konstitutive Gesetze beschreiben die Darstellung von zwei Speicherelementen und einem dissipativen Element. Diese Bauelemente können als ideale konzentrierte Ersatzelemente aufgefasst werden. Wir nennen sie Induktivität, Kapazität und Widerstand.
Eine komplette Übersicht des bisherigen Inhaltes zeigt die die folgende Abbildung. Sie kann auch hier als PDF geladen werden.
Physikalische Teilsysteme
In diesem Abschnitt werden mechatronischen Zweitore sowie ihre Anwendung im Simulationssystem behandelt. Im Allgemeinen wird es sich sogar um lineare Eintore handeln. Bei Besonderheiten, wie zum Beispiel Nichtlinearitäten oder Modellen mit tatsächlichem Zweitorcharakter, wird gesondert darauf hingewiesen. Die Bedienung und Arbeitsweise der Simulationsumgebung LTSpice wird dabei weitgehend vorausgesetzt. Nur dort, wo es explizit notwendig erscheint, werden spezielle Hinweise für die Bedienung gegeben.
Alle hier in diesem Abschnitt verwendeten Modelle und Symbole sind der Bibliothek Mechatronik.lib zu finden. Weiterhin gibt es ein Tutorial zum Einsatz und zur Anwendung der einzelnen Baudelemente. Ausführliche und detaillierte Aufgabenstellungen und Problemlösungen können in der entsprechenden Literatur [4]nachgelesen werden.
Mechanik - Translation
träge Masse - Kapazität
Das ideale mechanische Bauelement träge Masse speichert als ideale Kapazität nur P-Energie. Da die Kapazität selbst keine dissipativen Eigenschaften besitzt, beinhaltet sie auch keine Leistungsverluste in Form von Prozessleistung.
| Beschreibung | Größe | Variable | Formelzeichen | Einheit |
|---|---|---|---|---|
| Bauelement | träge Masse | Cm | mT | kg |
| Flussgröße | Kraft | IX | F | N |
| Differenzgröße | Geschwindigkeit | Y | v | m/s |
Anmerkung
Die träge Masse ist im Allgemeinen kein erdfreies Bauelement. Das bedeutet, dass alle in einem mechatronischen Netzwerk vorhandenen Massen in einem Punkt verbunden sind. Dieser Punkt hat immer die Geschwindigkeit null.
| Symbol | mechanisch | 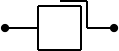
|
| Symbol | allgemein | 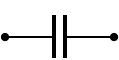
|
| LTSpice | C_m_p | Mechatronik.lib |
Nachgiebigkeit - Induktivität
Die mechanische Steifigkeit ist eine physikalische Größe, die eng mit der höheren Festigkeitslehre verknüpft ist. Sie lässt sich im Allgemeinen nicht durch eine einfache Gleichung beschreiben. Vielmehr ist sie ein Maß dafür, wie ein Körper auf äußere Beanspruchungen mit elastischen Verformungen reagiert. Somit hängt die Steifigkeit eines mechanischen Bauteils nicht nur von den elastischen Eigenschaften des Werkstoffes ab, sondern auch stark von der Geometrie des Bauteils. Der Kehrwert der absoluten Steifigkeit wird auch Nachgiebigkeit genannt. Im allgemeinen Belastungsfall ist eine einfache Trennung der Steifigkeit nach den Belastungsarten jedoch nicht mehr möglich. Die zu ermittelnden Steifigkeiten bilden dann einen Steifigkeitstensor. Um mittels mechatronischer Netzwerke dennoch eine Simulation durchführen zu können, wird ein stark vereinfachtes Bauelement, die mechanische Induktivität, eingeführt. Das ideale mechanische Bauelement Steifigkeit ist eine absolute Größe und speichert nur T-Energie. Da Reibungseigenschaften und Materialdämpfungen unberücksichtigt bleiben, beinhaltet die Steifigkeit keine Leistungsverluste in Form von Prozessleistung. Der linearelastische Zusammenhang gilt immer nur in einer Bewegungsrichtung. Kopplungen, die durch räumliche Verzerrungen auftreten, werden nicht berücksichtigt.
| Beschreibung | Größe | Variable | Formelzeichen | Einheit |
|---|---|---|---|---|
| Bauelement | Nachgiebigkeit | Lm | n | m/N |
| Flussgröße | Kraft | IX | F | N |
| Differenzgröße | Geschwindigkeit | Y | v | m/s |
Anmerkung
In der Mechanik und im Maschinenbau wird häufig mit der inversen Nachgiebigkeit, der Steifigkeit gearbeitet. Das Bibliothekselement bildet deshalb die Steifigkeit ab.
| Symbol | mechanisch | |
| Symbol | allgemein | |
| LTSpice | L_m_p | Mechatronik.lib |
Dämpfung - Widerstand
Unter einem mechanischen Widerstand verstehen wir ein passives, rein dissipatives Bauelement. Die Dissipation ist dabei ein Prozess, bei dem Energie zerstreut und in Entropie umgewandelt wird. In der Mechanik spricht man auch von Dämpfung. Dämpfungsursachen können dabei sehr vielfältig sein und sowohl auf makroskopischen als auch auf mikroskopischen Effekten beruhen. Makroskopische Effekte sind zum Beispiel eine äußere Reibung oder Strömungen zwischen Festkörpern. Mikroskopische Effekte beschreiben das Materialverhalten in Form von innerer Reibung oder Plastizität. Neben dem Hook'schen Gesetz beobachten wir bei vielen Materialien auch ein Verhalten, das als Newton'sche Flüssigkeit bezeichnet wird. Die Spannungen verhalten sich hierbei proportional zur Dehnungsgeschwindigkeit. Genau dieses Verhalten entspricht dem geforderten dissipativen Prozess für einen Widerstand. Das ideale Bauelement Widerstand (Dämpfung) ist nur eine Komponente der Materialeigenschaften mechanischer Systeme. Da dabei die elastischen Eigenschaften vernachlässigt werden, beinhaltet die Komponente Dämpfung keinerlei Energiespeicher. Vielmehr wird die dissipative Energie vollständig in Entropie gewandelt.
| Beschreibung | Größe | Variable | Formelzeichen | Einheit |
|---|---|---|---|---|
| Bauelement | Dämpfung | Rm | d | m/Ns |
| Flussgröße | Kraft | IX | F | N |
| Differenzgröße | Geschwindigkeit | Y | v | m/s |
Anmerkung
In der Mechanik und im Maschinenbau wird häufig mit der inversen Dämpfung, der Dämpfungskonstante k gearbeitet. Das Bibliothekselement bildet deshalb die Dämpfungskonstante k ab.
| Symbol | mechanisch | |
| Symbol | allgemein | |
| LTSpice | R_m_p | Mechatronik.lib |
NEWTON'sche Reibung - nichtlinearer Widerstand
Ein lineares Widerstandsgesetz ist für viele technische Anwendungen oft eine Ausnahme. Meist finden wir eher Zusammenhänge, welche sich nur um einen Punkt linear abbilden lassen. Analysiert man die unterschiedlichen physikalischen Widerstandsgesetze in der Mechanik, so fällt ein grundlegender Zusammenhang auf.
In der Mechanik nennen wir diesen Zusammenhang auch die Newton'sche Reibung.
Die konstitutiven Gesetze der mechatronischen Netzwerke bauen auf einem linearen Leistungsgesetz auf.
Das bedeutet, dass die Leistung in einer physikalischen Domäne immer aus dem Produkt der Potentialdifferenz über einem Widerstand mal dem Fluss durch diesen Widerstand bestimmt wird, egal wie die innere physikalische Beschaffenheit dieses Widerstandes aussieht. Diesem linearen Leistungsgesetz muss auch in der Modellbildung der mechatronischen Netzwerke Rechnung getragen werden.
Für die Abbildung im Simulationssystem ist ein nichtlineares Widerstandsgesetz in Abhängigkeit der Potentialdifferenz günstiger.
Übungsaufgabe 2.1
Ein Fahrzeug mit der Masse mA = 1500 kg fährt mit einer Geschwindigkeit vA = 100 km/h über eine wellige Straße. Wie groß ist die senkrecht zur Straße wirkende Schwingbeschleunigung des Fahrzeuges?
Analysemodell
Im Modell wird die Fahrzeugmasse als starrer Körper angenommen. Alle vier Federbeine, bestehend aus Stoßdämpfer und Feder, werden als Kelvinkörper zusammengefasst. Die Räder selbst sind masselos. Die Welligkeit der Straße wirkt sich als Erregergröße sowohl auf die Feder als auch auf den Dämpfer aus.
Lösung
Analytisch könnte die zugehörige Differentialgleichung über den Impulssatz aufgestellt und gelöst werden.
Dieser Weg soll hier jedoch nicht verwendet werden. Vielmehr lösen wir die Aufgabenstellung mittels der zuvor eingeführten Bauelemente.
Die Feder (Induktivität) wird mit dem Dämpfer (Widerstand) parallelgeschaltet (Kelvin Körper). An einem Knoten ist die Fahrzeugmasse als starrer Körper befestigt. Der zweite Bezugspunkt des starren Körpers liegt auf Masse. Die Bodenbewegung durch die Welligkeit der Straße kann zunächst als Wegerregung mit einer maximalen Wegamplitude und einer Erregerfrequenz interpretiert werden. Diese greift direkt an der Feder an (wegproportionale Federkraft). Da die Dämpferkraft selbst geschwindigkeitsproportional ist, muss die Wegerregung einmal differenziert werden um als Geschwindigkeitserregung am Dämpfer zu wirken. Im Simulationsmodell schwingt die Masse nun mit einer bestimmten Geschwindigkeit (Spannung entspricht der Schwinggeschwindigkeit). Da jedoch nach der Schwingbeschleunigung des Fahrzeuges gefragt ist, muss die Schwinggeschwindigkeit nochmals differenziert werden.
Übungsaufgabe 2.2
Im Schwerefeld der Erde (konstante Erdbeschleunigung) fällt eine Stahlkugel im freien Fall (Anfangsgeschwindigkeit v=0) nur gebremst durch die NEWTON’sche Reibung (geschwindigkeitsquadratische Reibung). Wie sieht der Verlauf der Fallgeschwindigkeit über die Zeit aus? Welche Grenzgeschwindigkeit erreicht die Stahlkugel?
Analysemodell
Im Modell wird die Stahlkugel als starrer Körper angenommen. Sowohl die Dichte der Luft als auch die Erdbeschleunigung sollen über die gesamte Fallhöhe als konstant angenommen werden. Es wirkt ausschließlich NEWTON’sche Reibung an der Kugel.
Lösung
Analytisch könnte die zugehörige Differentialgleichung über den Impulssatz aufgestellt und über Trennung der Variablen gelöst werden.
Dieser Weg soll hier jedoch nicht verwendet werden. Vielmehr lösen wir die Aufgabenstellung mittels der zuvor eingeführten Bauelemente, sowie des nichtlinearen Widerstandes. Die Kugelmasse wird über eine Kapazität simuliert. Da die Erdbeschleunigung als konstant angenommen wird, kann sie sehr einfach durch eine Stromquelle abgebildet werden. Für die NEWTON’sche Reibung setzen wir einen nichtlinearen Widerstand mit dem Exponenten 2 ein.
Anmerkung
Bei der Simulation mittels LTspice muss natürlich beachtet werden, dass die Geschwindigkeit in „Volt“ ausgegeben wird. Da jedoch prinzipiell SI-Einheiten verwendet werden, entspricht 1V = 1m/s. Die Grenzgeschwindigkeit der fallenden Kugel beträgt also 47.63 m/s oder 171.5 km/h.
Nachricht an den Autor:
Downloads
Multi-Domän-Systeme auf einen Blick
LTSpice Bibliothek Mechatronik.lib
Links
Übungsaufgaben & Simulationsdateien
Quellen
- ↑ Rüdiger G.Ballas, Günther Pfeifer und Roland Werthschützky: Elektromechanische Systeme der Mikrotechnik und Mechatronik: Dynamischer Entwurf – Grundlagen und Anwendungen. 2. Auflage. Springer, 2009, ISBN 978-3-540-89317-2, S.11.
- ↑ Jörg Grabow: Verallgemeinerte Netzwerke in der Mechatronik. 1. Auflage. Oldenbourg Wissenschaftsverlag, 2013, ISBN 978-3-486-71261-2, S.I.
- ↑ Robert H. Bishop: Mechatronics: An Introduction. CRC Press, 2005, ISBN 1-4200-3724-2, S.8.4.
- ↑ Jörg Grabow: Mechatronische Netzwerke: Praxis und Anwendungen (De Gruyter Studium). De Gruyter Oldenbourg 2018, ISBN-13: 978-3110470840