Digitaler Rauschgenerator im FPGA

Aus der Mikrocontroller.net Artikelsammlung, mit Beiträgen verschiedener Autoren (siehe Versionsgeschichte)
Wechseln zu: Navigation, Suche

Ein digitaler Rauschgenerator basierend auf Zufallsbits

von J.S.

Dieser Artikel beschreibt eine Möglichkeit, tatsächlich zufällige, nicht vorhersagbare Bitfolgen zu erzeugen, die prinzipiell gleichverteilt sind und keinerlei Präferenzen besitzen. Damit lassen sich tatsächliche Zufallszahlen erzeugen, die wiederum als Rauschen verwendbar sind.

Für die Realisation in VHDL müssen noch Buffer eingesetzt- sowie Schaltungsteile mittels "keep" erhalten werden. Die Lösung ist so gewählt, dass keine PLLs oder eine externe Verschaltungen benötigt werden.

Historie

Rückgekoppelte Schieberegister- und Inverterstufen unterschiedlichster Art sind seit Beginn der Digitaltechnik bekannt. Einige Spezialversionen von Verknüpfungen unterschiedlicher Quellen über u.a. EXOR-Glieder sowie implizite Symmetrierungen sind Gegenstand von Patenten.

Diese hier vorgestellte Schaltung arbeitete seinerzeit mit real aufgebauten CMOS-Invertern und einem Binärzähler der 4000er Serie. Das letzte Bits diente als Umschalter zwischen den unterschiedlich langen Inverterketten. Die Grundidee dazu war um 1995 herum Gegenstand eines Laborexperimentes für Studenten der Elektrotechnik der Universität Siegen und würde später in einem PLD als Rauschgenerator zum Dithern verwendet. Die weitergehende Methode der sich gegenseitig selbständig umschaltenten Inverterketten ist von mir, meines Wissens nicht patentiert und hiermit ausdrücklich frei zur Verwendung. Sie wurde erstmalig um 2005 herum in einem FPGA eingesetzt - ebenfalls als Dither- und Klangquelle.

Die Idee der regelmäßigen oder auch unregelmäßigen Umschaltung der Bitfolgen über EXOR mit dem Ziel des statistischen Ausgleichs der Nullen und Einsen ist ebenfalls nach meinem Wissen nicht patentrechtlich geschützt.

Prinzip

Die Idee beruht auf der Abtastung eines sich asynchron zur Zieldomain bewegenden Taktes, der sich praktisch während jedes denkbaren Abtastvorgangs ändern und damit vollkommen zufällige Werte annehmen kann. Die so abgetasteten Bits werden dann unabhängig von einander zu Bytes zusammengebaut, wodurch prinzipiell auch lange Einsen- und Nullfolgen entstehen können. Dazu muss der asynchrone Takt allerdings vergleichsweise langsam abgetastet werden.

Der freilaufende Zähler

Eine einfache Schaltung für den Bitgenerator in VHDL ergibt sich durch einen Zähler, von dem ein Takt (hier 1/8-tel - es klappt oft auch 1/4-tel) abgeleitet wird und der sich infolge der aynchronen Rückkopplung auch noch verzählen kann:

signal toggle : std_logic_vector(2 downto 0) := "000";

signal clock  : std_logic;

p_osc : process (toggle)

begin 

 toggle <= toggle + "1";
 clock <= toggle (2);

end process;

Die Teilung des Taktes ist bei manchen FPGAs nicht nötig, allerdings wird eine simple Rückkopplung vom Typ toggle <= not toggle; mitunter nicht erzeugt, bzw. sie ist zu schnell, um einen sauberen Takt zu erzeugen. Je breiter der Vektor "toggle" angesetzt wird, desto grösser ist die Wahrscheinlichkeit, dass der Zähler falsch zählt und Periodensprünge vollzieht. Die Ausgangsfrequenz wird allerdings geringer. Diese einfache Formulierung führt aber zu sehr technologieabhängigen Implementierungen, die von Synthesedurchlauf zu Synthesedurchlauf schwankt. Ein Beispiel findet sich im Farbmultiplex-Modul meines VGA-Cores.

Besser ist ein gezielter Aufbau eines selbstschwingenden Systems auf Technologieniveau:

Einfacher Ringoszillator

Der naheliegende Ansatz ist ein selbstschwingender Ringoszillator, der unabhängig von der Zieldomain arbeitet und im Prinzip jeden Flankenzustand darstellen kann. Derartige Oszillatoren lassen sich leicht durch rückgekoppelte Inverterketten bilden, die vom Prinzip nie in einen stabilen Zustand schwingen können und daher immer oszillieren. Gegenüber dem Zähler werden höhere Taktraten erzielt. Die Erfahrung zeigt aber, dass solch ein einfacher Oszillator meistens nicht genügend jittert, um über venüftige Zeiträume wirklich alle erdenklichen Kombinationen erzeugen zu können, da sich in der kurzfristigen Betrachtung immer eine Interferenz zu dem Abtasttakt einstellen wird. Ausserdem zeigt sich, dass solche Ringoszillatoren dazu neigen, sich auf benachbarte Schaltungsteile zu synchronisieren. Wenn diese mit dem Lesetakt getriggert werden, entstehen beobachtbare Spektren in den erzeugten Bitfolgen.

Mehrfach-Ringoszillator

Eine deutliche Verbesserung stellt die Verwendung zweier Oszillatoren dar, die miteinander interferieren und je nach zeitlicher Überlagerung durch Verknüpfung mit einem EXOR ein z.T. sehr schnell toggelndes Bit ergeben, das schon gute Zufallswerte generiert, wenn es selten genug abgetastet wird. Je mehr solche Oszillatoren zugeschaltet werden, desto größer ist die Wahrscheinlichkeit eines Bitwechsels im Bereich der abtastenden Flanke. Leider neigt aber auch diese Anordnung von Ringoszillatoren dazu, sich auf Einflüsse der Restschaltung zu synchronisieren, was sich in der FFT-Analyse und Häufungsmessung des erzeugten Ausgangsignal äussert.

Desynchronisierte Ringoszillatoren

Eine effektive Möglichkeit, etwaige Synchronisationsneigungen zu unterdrücken, ist es, die Frequenzen der Oszillatoren permanent umzuschalten, sodass keiner von ihnen eine stabile Phasenlage einnehmen kann. Genau, wie zu Beginn der Einschwingphase, benötigt der Oszillator nach dem Umschalten nämlich einige Schwingungen, um halbwegs stabil zu werden. Dies gilt insbesondere, wenn er sich auf irgendein externes Ereignis einstellen möchte. Wenn rechtzeitig umgeschaltet wird, hat der Oszillator keine Chance, sich auf Nachbarschaltungen einzuschwingen.

Die Umschaltung funktioniert so, dass die Länge der Inverterkette verändert wird, indem ein Steuersignal einen Multiplexer treibt, der zwischen zwei Pfaden auswählt. Im einfachsten Fall schaltet man einfach 2 Inverter mehr dazu, wodurch sich etwas die Frequenz senkt. Je nach Technologie sind 4 Inverter besser, da dies einen deutlicheren Frquenzhub zur Folge hat. Entscheidend ist bei der Methode auch, dass durch das Umschalten ein Phasensprung erzeugt wird. Sollte der Oszillator begonnen haben, sich auf ein Ereignis zu synchronisieren, wird die massgebliche Taktflanke dadurch sofort wieder auf einen anderen Punkt gesetzt.

selbstdesynchronisierende Ringoszillatoren

Eine Erweiterung der Lösung von oben ist es nun, die Zeitpunkte der Umschaltung ebenfalls zufällig bestimmen zu lassen. Dies geschieht am einfachsten durch einen ähnlich aufgebauten Gegenpart, der seinerseits wieder zufällig gesteuert wird. Im ersten Schritt entsteht der nachfolgend beschriebene 2fach- gekoppelte OSC. Mit drei deratig ringförmig verketteten, selbstschwingenden Oszillatoren bekommt man ein nahezu zufälliges Verhalten der Phase, da sich immer einer der Oszillatoren im Einschwingvorgang befindet und sich sein Beitrag zum Exor stark verschiebt, sodass auch in der lokalen Betrachtung keine sichtbaren Interferenzmuster mehr auftreten.

Realisationsvorschlag

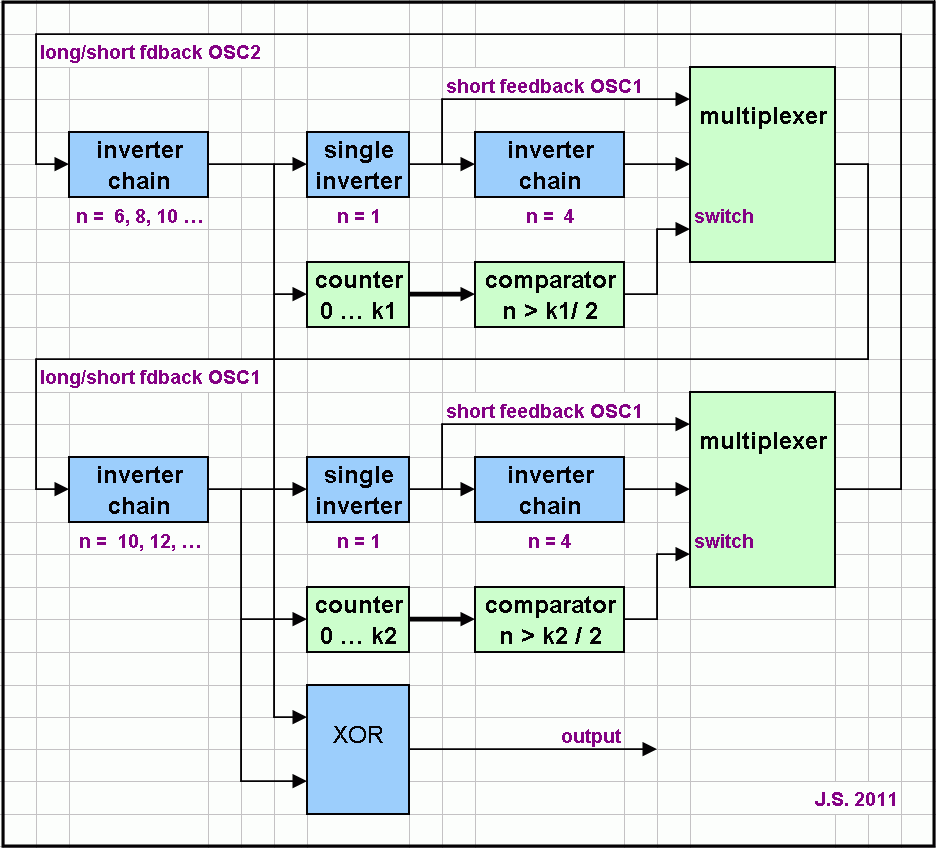
Hier eine konkrete Lösung mit 2 gekoppelten Oszillatoren:

Js-Vhdl-noise-bit-generator-schematic.gif

Jeder der beiden OSC wird über eine Inverterkette mit einer insgesamt ungeraden Anzahl von Invertern gebildet, wobei die geradzahligen Inverterstufen ein delay bilden. Die Rückführung erfolgt über einen Multiplexer, welcher umschaltbar ist. So liegen beispielsweise einmal 7 und einmal 9 inverter in der Kette, bei dem anderen z.B. 11 oder 13.

Jeder der beiden Oszillatoren treibt einen eigenen Zähler an, der bis 13 bzw. 27 zählt. Das jeweilige höchste Bit des Zählers wird zum Umschalten der Kettenlänge des anderen Oszillators benutzt. Durch die asymmetrische Verteilung 8/13 zu 5/13 bzw. 16/27 zu 11/27 wird erreicht, dass es eine längere und eine kürzere Phase gibt. Während der längeren Phase schaltet man die niedrigere Frequenz, während der längeren die höhere Frequenz. Damit ergibt sich für die Kettenlänge die Folge:

OSC1 : ...7.7.7.9.9.9.9.9.9.9.9.9.9.9.9.9.9.9.9.7.7.7.7.7.7.7.7.7.7.7.9.9.9.9.....

OSC2 : ....13.13.11.11.11.11.11.11.11.11.13.13.13.13.13.11.11.11.11.11.11.11.11.13.13...

Oszillator 1 darf also abwechselnd eine längere Periode mit der etwas niedrigeren Frequenz schwingen und danach eine kürzere Periode mit der höheren. Irgendwann dazwischen schaltet er die Frequenz des zweiten um. Da sich der andere ebenso verhält, ergeben sich grob 4 Frequenzkombinationen, die unterschiedlich und veränderlich überlappen. Durch die langen Phasen von mindestens >5 Takten ist sichergestellt, dass auch bei schnellen Technologien der jeweilige OSC wieder anschwingt, falls beim Umschalten mitten in einen Zustandswechsel gesprungen wurde. Genau dies verschiebt die Phasen immer wieder sehr zufällig, sodass die Frequenz nicht lange stabil ist und sich die Oszillatoren auf nicht auf Umgebungseinflüsse synchronisieren können. Die Ausgänge werden mit Exor gemischt, wodurch bei einer Abtastung durch eine andere Domain noch bis zu 5-10 MHz vollkommen zufällige Bits entstehen.

Realisation für Consumerqualität

16Bit-Rauschwerte bekommt man gemäß der Methode oben dann mit etwa 500kHz, in dem man kontinuierlich samplet und die Werte in SR schiebt. Für meine Audioworkstation benutze ich eine Abtastrate von ~4,5MHz und generiere daraus 24 Bit-Werte mit 192kHz Samplefrequenz. Muster im Bereich der Audiofrequenzen sind im Spektrum nicht erkennbar.

Anfänglich hatte ich auch noch mehrere Generatoren parallel aufgebaut und die 24 Bit-Werte gemischt, fand aber keine Verbesserung mehr. Allerdings hatte ich teilweise den Fall, dass statistisch mehr Nullen rauskamen (53%:47%). Ich habe dann einfach zwei ähnliche Generatoren aufgebaut (andere Kettenlängen) und einen Kanal invers zugemischt. Für meine Zwecke reicht das jetzt vollkommen aus. Für messtechnische Zwecke müsste man es näher untersuchen. Wenn man irgendwelche Rauschquellen mischen möchte, sollte man eine Extraquelle aufbauen, statt die erste mit anzuzapfen, es sei denn, dies ist signalverarbeitungstechnisch notwenig. Bei den Tongeneration von Schlagzeugklängen bekam ich vereinzelt seltsame metallisch klingende Auslöschungen, wenn zwei Instrumente (per Filter erzeugt) gleichzeitig erklangen. Einfache Abhilfe schafft ein Bitvertauscher.

Realisation für Messtechnik

Für messtechnische Applikationen sollte man genügend niedrig abtasten, z.B. 1/MHz/bit. Für jedes weitere bit bzw MHz kommt ein weiterer Generator hinzu, der anders parametriert ist. Das stellt platzmäßig nur ein geringes Problem dar, da je nach Realisation nur 50-100 Logikelemente benötigt werden. Die Rauschgeneratoren sollten an verschiedenen Stellen im FPGA sitzen und sich keine Logikzellen teilen -> FPGA-Editor für das mapping / constraints benutzen.

Ein eventuelles 1:0-Verteilungsproblem sollte mit zwei komplementären Rauschquellen zu lösen sein, während man die Zuordnung der Rauschbits ebenfalls noch ändern kann, indem man einen weiteren Oszillator nutzt, der zyklisch Adressen generiert, die einen von mehreren Multiplexern mit wechselndem Bitmapping auswählt. Auch lassen sich mehrere Rauschgeneratoren überlagern, um die Auflösung zu erhöhen. wobei das Problem auftritt, dass Ergebnisse im mittleren Wertebereich dann wahrscheinlicher sind, als Werte am Rand. Will man das verhindern, sind die Werte immer über EXOR bitweise zu verknüpfen.

Bauvorschlag / Beispiel

Ein array von 2x32 Rauschquellen (ca. 500 LEs) wird mit einem PLL-basierten Takt von 1MHz in 64 Registern asynchron eingelesen. Über einen 64:64-Bitvertauscher mit zufällig wechselndem Mapping werden diese zu zwei 32 2-Bit-Werten zusammengesetzt, die mit einem Exor und einem Inverter von einander subtrahiert / komplementär addiert werden. Die Ergebnisse gehen auf einen synchronen asymmetrischen 32:8-FiFo, der 8-bit Rauschwerte mit 4MHz produziert, die statistisch vollkommen gleichverteilt sind.

Einschätzung der Qualität

Simulation

Bereits mit festen Werten für die Inverterverzögerungen, die ja real starken Zufällen unterworfen sind, produziert eine ModelSIM-Simulation für die 2fach-Lösung ein sehr komplexes Muster mit geringer Wiederholrate. In der Realität lässt sich ein entsprechender Jitter messen, der mehrere Perioden des abtastenden Taktes überstreicht.

Mit einer analogen Simulation können minimale Änderungen des Schaltverhaltens untersucht werden. Variiert man z.B. die Steilheit nur eines Inverterausgangs eines Oszillators um 0,5% ergibt sich bereits nach wenigen Schwingungen ein qualitativ verändertes Bild, weil die Umschaltpunkte des anderen Oszillators ein wenig wandern, wodurch sich eine andere Phasenkonstellation ergibt.

  • 2 Fälle verkoppelter Oszillatoren
  • Die beiden blauen Oszillatoren variieren minimal, was anhand des sich ergebenden 2Bit Codes (Visualisierung der Zustandsfolge) = violette Kurve schon sichtbar wird. Der mit einem EXOR gebildete Signal-Wert (türkis), wird mit einem willkürlichen Takt im FPGA (rot) gesampelt, sodass der grüne Ausgangswert entsteht. Eine kleine Änderung im Verhalten eines Inverters bedingt bereits ein anderes Ausgangsmuster;

Probleme der realen Schaltung

Leider ergibt sich das Problem, dass bei zusammenfallenden Flankenwechseln kein eindeutiges Signal am Ausgang des XOR-Gatters erzeug wird und das abtastende FF der Zieldomain einen Zwischenwert sieht. Aufgrund der nicht 100%-symmetrischen Schaltungstopologie in CMOS-Schaltungen liegt die Schaltschwelle für den FF-Eingang nicht auf dem 50%-Niveau, sodass mitunter ein Zustand (0 oder 1) bevorzugt wird und häufiger auftritt. Dieses Prblem lässt sich durch einen Twister lösen:

Twister als Symmetierhilfe

Durch Zuschaltung eines weiteren ca Faktor 8-16 langsamer laufenden Zufallsbitgenerators wird die Bedeutung eines Bits bei Zustand 1 invertiert, was durch ein weiteres XOR realisiert wird. Damit unterdrückt eine hohe Zahl von Einsen sich selbst. Die statistische Verteilung der Zahlen wird damit quasi umgeklappt. Angenommen, ein asymmetrischer Generator liefert zu 60% Einsen und nur 40% Nullen, so würde ein weiterer Generator derselben Art jeweils 60% der Bits invertieren. Es ergäben sich also:

  • 60% * 60% = 36% zu 0 (1 verändert)
  • 40% * 60% = 24% zu 1 (0 verändert)
  • 60% * 40% = 24% zu 1 (1 unverändert)
  • 40% * 40% = 16% zu 0 (0 unverändert)

im Ergebnis also 36%+16% = 52% Nullen und 48% Einsen und damit erheblich symmetrischer, als die Eingangsannahme. Der Twister hat sich in einem anderen Zusammenhang praktisch bereits vervorragend bewährt und eigenet sich auch für andere Formen von Zufallsgeneratoren.

Messungen

  • FFT-Analyse von 2 gekoppelten Oszillatoren
  • Das Bild (Screenshot) zeigt eine FFT-Analyse von künstlich erzeugtem 16Bit-Rauschen aus zwei gekoppelten Oszillatoren. Der blaue Bereich zeigt die spiegelsymmetische 1024 FFT bei 16Mhz. Links sind Min, Max, Mittelwert und Standardabweichung automatisch markiert. Der verkleinerte türkise Bereich zeigt die um Faktor 2 verkleinerten über 16 Messungen gemittelten Werte.;

Tauglichkeit als Zufallszahlengenerator

Die so erzeugten Zufallsbits reichen in aller der Regel bereits für gute Zufallszahlen aus, wie sie in Simulationen für technische Anwendungen benötigt werden. Sie entstehen durch einfaches Aneinanderreihen von mehreren Bits mit einem Schieberegister.

Gleichverteilung

Das Aneinanderreihen von Bits bevorzugt keine Zahl. Theoretisch kommt jede Zahl mit derselben Häufigkeit vor. Ausnahmen sind wie oben beschrieben technologisch bedingt und durch den Symmetrierer zu verbessern.

  • Verteilung der erzeugten Zahlen
  • Die Grafik zeigt die Verteilung von Zahlen, die mit einem Rauschgenerator generiert wurden. Mit 8 zusammengehängten Bits werden Zahlen erzeugt und deren Häufung mitgezählt, wobei dieselbe Zahl innerhalb von 4096 "Würfen" schwerpunktmäßig etwa 10-40x vorkommt. Wird das Experiment fortgesetzt und weitersummiert, gleichen sich Unsymmetrien wieder etwas aus und die Kurve wird glatter. Bei 15000 Würfen beträgt die Dynamik zwischen seltenen und häufigen Zahlen ca. 60-120. Die Varianz beträgt letzlich nach >250.000 Würfen noch etwa +/- 12%. Aus Platzgründen sind nur die ersten 128 Zahlen dargestellt.;

Normalverteilung

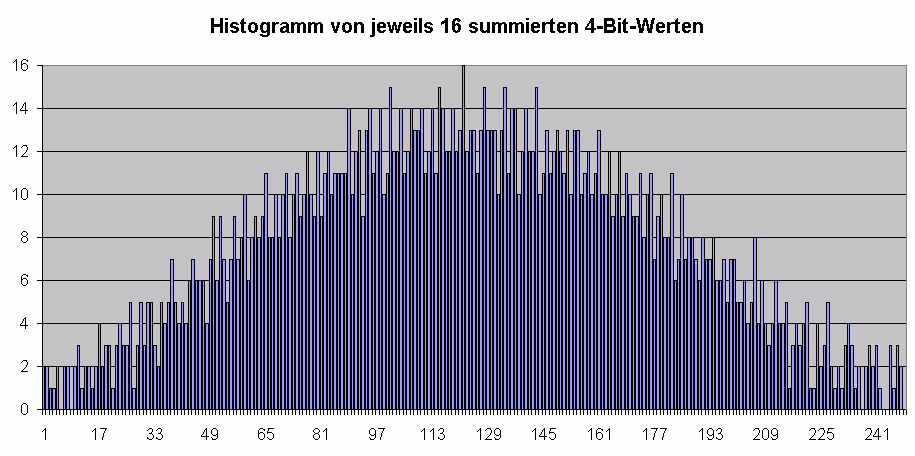
Durch das Addieren von Rauschwerten kommen Werte in der Mitte des Zahlenraums naturgemäß häufiger häufiger vor, weil es mehrere Kombinationsmöglichkeiten gibt, wie sie entstehen können. Werte am Randbereich sind sehr selten. Js-histogramm-rauschgenerator-summe.gif

Um den 8-Bit Zahlenraum abzudecken, wurde für den Rundungsfehler eine weitere Zahl addiert. Damit ist der Zahlenraum 0...255 darstellbar. Ansonsten wären nur 16x15 = 240 erreichbar.

Weitere Verteilungen

Will man gezielte Verteilungen generieren und sicherstellen, dass Zahlen nach bestimmten Zeiten mindestens einmal auftreten, muss noch ein wenig mehr getan werden. Siehe Digitaler Zufallszahlengenerator in VHDL.

Verbesserungsmöglichkeiten

Um die Zufälligkeit weiter zu erhöhen, lässt sich die Schleife eines oder mehrerer Oszillatoren über externe Pins bilden, was zu starken Temperatur und Exemplarschwankungen führt. Dies ist vor allem bei der Nutzung nur eines Oszillators vorteilhaft. Allerdings reduziert sich dadurch die maximale Frequenz des Generators.

Tauglichkeit als Rauschgenerator

Aufgrund der echten Zufälligkeit der Werte können keine Aussagen über das Spektralverhalten gemacht werden, womit sich das System als nichtdeterministischer Rauschgenerator eignet. Im Test wurden keine bevorzugt erzeugten Frequenzen beobachtet.


Anwendungen

Signalverarbeitung

Echte Zufallszahlen werden oft als Startwerte für deterministische Zufallszahlengeneratoren verwendet. Solche Generatoren kommen z.B. bei der Verschlüsselung von Signalen zur Anwendung. Um sie praktisch nutzen zu können, müssen sie selbstverständlich beiden Stellen (Encoder und Decoder) bekannt sein.

Bildverarbeitung

Rauschgeneratoren werden in der Bildverarbeitung zur Verbesserung der Bildqualität eingesetzt, indem z.b. mittels der "salt and pepper"-Methode Kanten infolge von Abtastungsartefakten geglättet werden.

Beiträge zum Thema

externe Weblinks

Abgerufen von „https://www.mikrocontroller.net/index.php?title=Digitaler_Rauschgenerator_im_FPGA&oldid=97034“