Hilbert-Transformator (Phasenschieber) mit ATmega
Dieser Artikel ist eine Fortsetzung von Digitalfilter mit ATmega und behandelt ein spezielles Digitalfilter namens Hilbert-Transformator.
Neben den üblichen Filtern, Tiefpass, Hochpass, Bandpass und Bandsperre, gibt es einige weitere Typen. In der Literatur findet man u.a. noch den Allpass, Phasenschieber, Integrator und Differentiator.
Der Hilbert-Transformator, ein Breitband-90-Grad-Phasenschieber
In den Lehrbüchern wird er völlig zu Unrecht eher am Rande abgehandelt. Tatsächlich findet man ihn in allen Schaltungen zur Datenübertragung, zu Modulation oder Demodulation mit I/Q-Mischern, im „Software-defined radio“.
Auch ein Hilbert-Transformator kann mithilfe von Scilab berechnet werden. Allerdings gibt es keine fertige Software, man muss sich durch einige Literatur hindurchfressen, z. B. ISBN 0471619957 Sanjit Mitra, Handbook for DSP (1993), Kapitel „Special Filter Designs“ von Phillip Regalia.
Matlab-Plots dazu hier ab Seitenzahl 41
GNU Octave stellt die Hilbert-Transformation und den Parks-McClellan-hilbert-FIR-Filterentwurf im octave-forge Paket "signal" zur Verfügung.
Eine Fundgrube sind die Matlab-Texte von Prof. Schüssler, die vorab 1998 zum zweiten Band seines Lehrbuchs auf seiner Webseite veröffentlicht wurden. Inzwischen ist der erste Band in der fünften Auflage erschienen ISBN 9783540782506 , der zweite Band ISBN 9783642011184 2010 erstmalig erschienen, Software-Download hier aber die Webseite ist nach seinem Tod 2007 abgeschaltet. Zum Glück gibt es das Webarchiv, wo die Texte noch zu finden sind.
Zu dieser Zeit waren die Matlab-Programme noch nicht in „Toolboxen“ untergebracht, deren Funktion von außen nicht mehr sichtbar ist. Daher lassen sie sich relativ einfach in Scilab oder Octave übersetzen.
Vier Versionen von Hilbert-Transformatoren werden hier berechnet:
- FIR-Hilbert, aufwendig, aber streng linearphasig, der bekannteste Typ, da schon lange mit dem Matlab-Befehl remez / firpm und Parameter 'hilbert' berechenbar. Mit dem octave-forge Paket "signal" ist remez mit "hilbert" verfügbar. Scilab kennt diesen Parameter nicht.
- näherungsweise linearphasiger IIR-Hilbert, maximal flach,
- näherungsweise linearphasiger IIR-Hilbert, Tschebyscheff
- minimalphasiger IIR-Hilbert, kompakt, aber mit großen Gruppenlaufzeitschwankungen, eher für Audioanwendungen als Digitalsignale.
Im Artikel von Schüßler/Steffen (siehe unten) sind in zwei vergleichenden Beispielen die Gruppenlaufzeitschwankungen des maximal Flachen etwa halb so groß, des Minimalphasigen etwa fünf Mal so groß wie die Tschbyscheff-Version.
Zumindest der kompakte IIR-Hilbert lässt sich auch in einem ATmega unterbringen. Er besteht aus einer Verzögerung und zwei Allpässen, die wieder aus SOS-Teilfiltern aufgebaut sind. Pro Teilfilter gibt es nur einen Koeffizienten, sodass man mindestens acht Teilfilter verwenden kann.
Ein Hilbert-Kochrezept (noch unvollständig)
Folgen wir dem Zahlenbeispiel und Berechnungsweg im „Handbook for DSP“.
Zuerst berechnen wir einen elliptischen Halbband-Tiefpass. Halbband besagt, dass die beiden Grenzfrequenzen symmetrisch zur halben Nyquist- Frequenz also 0,25 * Abtastfrequenz liegen, siehe Bild oben rechts. Die genauen Bedingungen lauten in der Schreibweise des Buches (p=passband, s=stopband):
- Omegas + Omegap = Pi
(auf Omegasample normierte Skala: Samplerate=2*Pi) - (1-Delta1)2 +Delta22=1
Als Zahlenwerte werden Omegas = 0,55*Pi und Delta2=0,01 gewählt, und damit ein elliptischer IIR-Tiefpass 7.Ordnung berechnet. Damit erhält er folgende Zahlenwerte der Pole:
0 0,436688 0,743707 0,927758
Scilab-Berechnung des Halbbandfilters
Mit Scilab erhalten wir nach einigem Ausprobieren praktisch dieselben Zahlenwerte, siehe Bild. Die Pole müssten für ein ideales Halbbandfilter genau auf der imaginären Achse liegen, der Realteil genau Null sein (Der Fehler kommt daher, dass die Angabe von fstop vom Programm nicht berücksichtigt wird, das Filter wäre überbestimmt). Diese Zahlen werden noch quadriert (konjugiert komplexe Pole zusammengefasst) und bilden schließlich die Koeffizienten des Hilbert-Transformators.
Die Übertragungsfunktion des gesuchten Hilbert-Transformators soll wie bisher H(z) heißen. Zur Unterscheidung nennen wir die bis jetzt berechnete Tiefpassfunktion G(z).
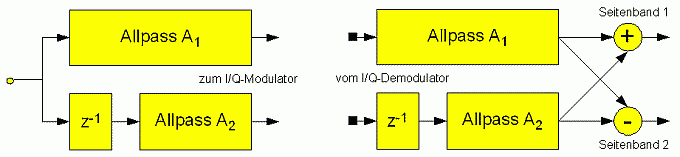
Wieder wird sie in SOS-Teilfilter aufgeteilt. Hier allerdings in die Summe von zwei parallel geschalteten Allpass-Funktionen A1 und A2 plus eine Verzögerung um einen Sampletakt, in der Übertragungsfunktion als „z-1“ ausgedrückt.
Ein Allpass läßt alle Signalfrequenzen mit unveränderter Amplitude durch, verändert nur die Phase. Seine SOS-Teilfunktion ist besonders einfach aufgebaut, zwei Koeffizienten sind Null, zwei sind gleich Eins und die beiden restlichen identisch. Damit benötigt man nur eine Multiplikation pro Teilfilter.
Die Tiefpass-Übertragungsfunktion erhält so die Form:
G(z) = ½ * ( A1 (z2) + z-1 * A2 (z2))
mit
[math]\displaystyle{ A_{1}(z^{2})=\frac{z^{-2}+0,190696}{1+0,190696\ast z^{-2}}\ast {\frac{z^{-2}+0,860735}{1+0,860735\ast z^{-2}}} }[/math]
[math]\displaystyle{ A_{2}(z^{2})=\frac{z^{-2}+0,553100}{1+0,553100\ast z^{-2}} }[/math]
Wenn man die beiden Ausgänge nicht addiert, sondern subtrahiert, entsteht ein Hochpass gleicher Grenzfrequenz. Beides kombiniert ergibt eine digitale Frequenzweiche.
Zum Übergang auf den Hilbert-Transformator ersetzen (substituieren) wir das z durch -jz und multiplizieren das ganze mit 2:
H(z)= 2*G(-jz)
H(z) = A1 (-z2) + j* z-1 * A2 (-z2)
mit
[math]\displaystyle{ A_{1}(-z^{2})=\frac{z^{-2}-0,190696}{1-0,190696\ast z^{-2}}\ast {\frac{z^{-2}-0,860735}{1-0,860735\ast z^{-2}}} }[/math]
[math]\displaystyle{ A_{2}(-z^{2})=\frac{z^{-2}-0,553100}{1-0,553100\ast z^{-2}} }[/math]
Wie man sieht, ändern sich nur die Vorzeichen. Die Pole liegen aber im Pol-Nullstellendiagramm auf der reellen Achse.
Die Ausgänge der beiden Allpässe sind jetzt gegeneinander um 90 Grad phasenverschoben, und können auf einen I/Q-Modulator gegeben werden. Umgekehrt kann man auch die beiden Eingänge auftrennen, und zwei um 90 Grad versetzte Signale aus einem I/Q-Demodulator einspeisen und die Ausgangssignale addieren oder subtrahieren, je nach gewünschtem Seitenband.
Und weil das so gut funktionierte, hier noch die Berechnung des Hilbert-Transformators von Olli Niemitalo mit einem Halbband-Tiefpass 17.Ordnung, was zu acht SOS-Teilfiltern führt, dazu folgt unten ein ATmega48-Programm.
Die originalen URL sind verwaist, aber im Webarchiv noch zu finden:
https://web.archive.org/web/20070719141658/http://yehar.com/ViewHome.pl?page=dsp/hilbert/
https://web.archive.org/web/20070814013543/http://yehar.com/ViewHome.pl?page=dsp/hilbert/011729.html
Olli ist auch heute (2019) noch aktiv:
http://yehar.com/blog/
speziell sein IIR-Hilbert:
http://yehar.com/blog/?p=368
Diskussion auch dazu:
https://dsp.stackexchange.com/questions/37411/iir-hilbert-transformer/59157#59157
Der näherungsweise linearphasige Hilbert-Transformator
Er wird im Handbook for DSP auf zwei Seiten sehr kurz abgehandelt. Statt aus zwei Allpässen besteht er aus einem einzigen, im anderen Zweig wird das Signal nur zeitverzögert, was mit einem Ringpuffer wenig Rechenzeit kostet. Eine Zeitverzögerung ist sozusagen die einfachste Form eines Allpasses, damit ist diese Bauform ein Spezialfall der oben gezeigten. Aus Schüsslers Texten erfahren wir noch, dass das Halbband-Tiefpassfilter zur Berechnung hier Tschebyscheff-Charakter haben muß.
Das Zahlenbeispiel zitiert Regalia aus einer anderen Veröffentlichung (M. Renfors and T. Saramäki, A class of approximately linear phase digital filters composed of allpass subfilters 1986 ) Der Allpass hat neun Koeffizienten, die Zeitverzögerung beträgt 17 Sampletakte. Der Halbband-Tiefpass hat eine Sperrdämpfung von > 49 dB. Sein Frequenzgang und der Phasengang des berechneten Hilbert-Transformators sind als Bild gezeigt.
Zum Allpass gibt es noch folgende Zahlenwerte:
Pole location for A(z)
z= -0.8699928078
0.491194141 ± j0.183666529
0.252724179 ± j0.463085544
-0.109950894 ± j0.548611467
-0.447326028 ± j0.356810323
Das könnte also ebenfalls noch in einen ATmega passen.
Hilbert ohne Multiplizierer
Eine interessante Variante wird im Artikel Design of multiplierless elliptic IIR halfband filters and Hilbert transformers vorgestellt. Ähnlich wie im Cordic-Algorithmus für trigonometrische Funktionen werden Multiplikationen vermieden, durch geschickte Wahl der Koeffizienten als Zweierpotenzen. Damit lässt sich der Phasenschieber auch in einem CPLD oder FPGA unterbringen.
Vom selben Autor gibt auch ein Buch von 2001 "Filter Design for Signal Processing Using MATLAB and Mathematica"
ISBN 9780201361308 mit einem Kapitel 9 ADVANCED DIGITAL FILTER DESIGN CASE STUDIES, in dem auch IIR-Hilbert-Filter behandelt werden. Auf Seite 432/433 ist derselbe multipliziererlose Hilbert zu finden.
Die beiden Allpässe des Zahlenbeispiels haben folgende Übertragungsfunktionen:
[math]\displaystyle{ \begin{align} A_1(z^{-2}) &=\frac{z^{-2}-0{,}12109375}{1-0{,}12109375 \cdot z^{-2}} \cdot\frac{z^{-2}-0{,}6640625}{1-0{,}6640625 \cdot z^{-2}} \\ &=\frac{z^{-2}-(\frac18 - \frac1{256})}{1-(\frac18 - \frac1{256}) \cdot z^{-2}} \cdot\frac{z^{-2}-(\frac12 + \frac18 + \frac1{32} + \frac1{128})}{1-(\frac12 + \frac18 + \frac1{32} + \frac1{128})\cdot z^{-2}}\\ \end{align} }[/math]
[math]\displaystyle{ \begin{align} A_2(z^{-2})\cdot{z^{-1}} &=z^{-1} \cdot\frac{z^{-2}-0{,}390625}{1-0{,}390625 \cdot z^{-2}} \cdot\frac{z^{-2}-0{,}890625}{1-0{,}890625 \cdot z^{-2}}\\ &=z^{-1} \cdot\frac{z^{-2}-(\frac14 + \frac18 + \frac1{64})}{1-(\frac14 + \frac18 + \frac1{64}) \cdot z^{-2}} \cdot\frac{z^{-2}-(1 - \frac18 + \frac1{64})}{1-(1 - \frac18 + \frac1{64}) \cdot z^{-2}} \end{align} }[/math]
Die ursprünglichen Zahlenwerte vor der Rundung auf Zweierpotenzen waren, wie auch im Artikel zu lesen:
0,1206 0,3900 0,6628 und 0,8906.
Im Artikel sind auch Kurven zur Abweichung zwischen den Idealwerten und den gerundeten abgebildet.
Hilbert Transformator nach der FIR-Methode
Nach dem Additionstheorem ergibt sich aus dem multiplikativen Mischen (u_prod = u_1 * u_2) zweier Wechselspannungen eine Überlagerung (u_sum = u_3 + u_4) zweier anderer Wechelspannungen; die Frequenz der einen Wechselspannung ist die Summe der Frequenzen der Faktor-Spannungen - die Frequenz der anderen Wechselspannung ist die Differenz der Frequenzen der Faktorspannungen. Jeweils eine der beiden Frequenzen ist das Nutz-Signal, die andere Frequenz ist die Spiegelfrequenz.
Der Hilbert-Tranformator ist ein Mittel um nur das Nutzsignal und nicht die Spiegelfrequenz zu mischen. Es wird nach den Regeln der Multiplikation komplexer Zahlen gemischt. Eingabesignal und Mischoszillator müssen in der Form der EULERschen Identität vorliegen:
y = A * exp( j * phi ) = A * ( cos( phi ) + j * sin( phi ) ) ; phi = omega * t ; omega = 2 * pi * f ; f ... Frequenz ; A ... Amplitude ; t ... Zeit
Mit der exp() - Darstellung kann man mischen, indem man den Ausdruck phi = 2 * pi * t * (f1 + f2) anwendet. Dabei addieren sich die Frequenzen ohne Spiegelfrequenz. Beide Frequenzen müssen als komplexe Zahlen vorliegen, also jede Frequenz als zwei Wechselspannungen mit (jeweils pro Frequenz) gleicher Amplitude. Liegt nur ein einfaches Sinus-Signal vor, kann man das dazugehörige Cosinus-Signal durch Phasenverschiebung um 90° mit einem Hilbert-Transformator erreichen. Danach wendet man die Multiplikation an:
y[ re, j * im ]:= x1[ re, j * im ]* x2[ re, j * im ] = (x1.re * x2.re - x1.im * x2.im) + j * (x1.re * x2.im + x2.re * x1.im) ; re ... Realteil ; im ... Imag. Teil
Jedes Glied des einen Faktors mit jedem Glied des anderen Faktors unter Beachtung der imaginären Einheit multiplizieren. Wendet man bei dem Signal einer der beiden Frequenzen nur einen der beiden Anteile (entweder nur realen Cosinus-Teil oder imaginären Sinusteil) so entsteht eine "negative" Frequenz (der Zeiger in der komplexen Zahlenebene dreht sich andersherum). Somit wird diese Frequenz von der anderen subtrahiert (phi = 2 * pi * t * (f1 - f2)). Das kann sowohl rechnerisch als auch durch Umpolen einer Bandfilterwicklung errreicht werden. Für Zwischenergebnisse nutzt man beide Signalteile weiter, für z.B. eine Audioausgabe genügt einer.
Kann man zu einem Sinussignal das Cosinus-Signal auch ohne synthetisches Filter erhalten? Genau weiß ich es nicht. Für einen Oszillator braucht man mindestens zwei Energiespeicher. Beide sind (wenn es kein Drehstromoszillator ist) um 90° phasenverschoben. Hier kommt man ohne synthetisches Filter aus. Anders bei Schallwellen. Der eine Speicher besteht hier sowohl aus Schalldruck als auch aus Schallschnelle. Sind beide um 0° phasenverschoben, so bewegt sich die Welle in die eine Richtung, bei 180° entsprechend entgegengesetzt. Der andere Speicher ist die 1. Ableitung von jeweils Schalldruck und Schallschnelle. Die Ableitung ist um 90° phasenverschoben aber bei frequenzabhängiger Amplitude ( y = A * sin( omega * t ) ; y' = omega * A * cos( omega * t ) ). Ohne Spiegelfrequenz kann man das nur für eine feste Frequenz mischen. Bei einem Frequenzband braucht man das synthetische Filter.
Der Hilbert-Transformator erzeugt aus einem Sinus-Signal das um 90° verschobene Cosinus-Signal. Ein Beispiel in Python:
# Begin Hilbert FIR filter.
import math # Math
import numpy as np # Math
import matplotlib as mlp # Plot
import matplotlib.pyplot as plt # Plot
FREQUENCY = 400.0 # 1 / s
RATE = 48000.0 # samples / s
SAMPLES = 4000
CELLS = 501
STEPS = SAMPLES - CELLS
PREFIX = (CELLS - 1) / 2
SUFFIX = CELLS - PREFIX
POSTFIX = SAMPLES - CELLS
samples = range(SAMPLES)
cells = range(CELLS)
steps = range(STEPS)
prefixes = range(PREFIX)
suffixes = range(SUFFIX)
postfixes = range(POSTFIX)
input = []
re = []
im = []
coefficients = []
def plot():
for sample in samples:
if(SAMPLES / 2 > sample):
_phi = FREQUENCY * sample / RATE * 2.0 * math.pi
else:
_phi = 5 * FREQUENCY * sample / RATE * 2.0 * math.pi
input.append(math.sin(_phi))
for cell in cells:
arg = cell - (CELLS - 1) / 2.0
if(0.0 == arg):
coefficients.append(0.0)
else:
arg *= math.pi
coefficients.append((1.0 - math.cos(arg)) / arg)
for postfix in postfixes:
coefficients.append(0.0)
for prefix in prefixes:
re.append(0.0)
im.append(0.0)
for step in steps:
re.append(input[step + PREFIX])
sum = 0.0
for cell in cells:
sum += input[step + cell] * coefficients[cell];
im.append(sum)
for suffix in suffixes:
re.append(0.0)
im.append(0.0)
# Prepare the plot.
plt.ylabel('amplitude')
plt.xlabel('timesteps')
plt.axis([0, SAMPLES - 1, -1.5, 1.5])
plt.grid(True)
plt.plot(samples, re, 'r-')
plt.plot(samples, im, 'b-')
plt.show()
# End.
Neben ein Array aus abgetasteten Werten eines akustischen Signales (hier Sinus-Signal, künstlich berechnet) wird das Array des Transformationskerns gelegt. Das Array des Transformationskerns ist dabei viel kürzer und es wird nur der gemeinsame Bereich berechnet. Der Wert des Cosinus-Signals, das zu dem Sinus-Signal gehört, das sich auf der Position der Mitte des Transformationskerns befindet, ergibt sich aus der Summe der Werte aus dem Sinus-Signal multiplizert mit den Faktoren aus dem Transformationskern mit gleichem Index. Das folgende Cosinus-Signal wird berechnet indem man zuvor den Transformationskern um einen Index gegenüber dem Eingabe-Sinus-Signal weiterschiebt (usw. bis zum Ende des Signales). Am Anfang und am Ende des berechneten Cosinus-Signales entsteht ein Stück Verlust der jeweils halb so lang wie der Transformationskern ist. Bei sehr lang dauernden Signalen (fast immer) ist statt dessen mit einem Ringpuffer zu arbeiten.
t ... Zeit
b[Länge k] ... Transformationskern
i[undendlich lang] ... Sinus - Signal oder Summe aus Sinus-Signalen
o[undendlich lang] ... um 90° verschobenes Cosinus - Signal
=>
o[t] := Summe { i[n+t] * b[n+t] } ; -k/2 <= n <= +k/2 ; t >= k/2
Der Transformationskern kann wie folgt ermittelt werden:
x ... natürliche Zahl > 0 k ... 4 * x + 1 b[] ... Transformationskern der Länge k n ... Index innerhalb des Tranformationskerns; -k/2 <= n <= +k/2 pi ... 3.14159... b[n] := ( 1 - cos( n * pi ) ) / ( n * pi ) ; Ausnahme ist b[0] := 0
Dabei ist das Argument der cos() - Funktion immer ganzzahlig. "1 - cos(...)" ist für ungerade "n" immer NULL. Der Kern hat nahe n == 0 maximale Werte und nimmt zum Rand hin ab. Ein Kern mit zuwenig Länge (k ist zu klein) wirkt als Hochpass und verkleinert die Amplitude von Signalen kleiner Frequenz (ist unbrauchbar). Kommen hohe und tiefe Frequenzen im Signal gleichzeitig vor, dann braucht man sowohl eine hohe Abtastrate als auch einen langen Kern ( k wird groß, z.B. Größenordnung 801 bei einem Audiosignal). Ändert sich das Nutzsignal unerwartet sprungartig so erhält man im Cosinus-Signal eine Art Sprungantwort.
- Großer Transformationskern : Medium:FIR_Kernel_Big.png
- Transformation zweier Signale verschiedener Frequenz : Medium:Hilber_FIR_OK.png
- Transformation eines Sprunges im Signal : Medium:Hilbert_FIR_OK_Lense.png
- Transformationsfehler bei zu kleinem Kern (k ist zu klein) : Medium:Hilbert_FIR_Too_Small_Kernel.png
Zusammenfassung Hilbert-Transformation ermittelt zu einem Sinus-Signal das um 90° verschobene Cosinus-Signal. Das gilt auch für eine Summe von Sinussignalen unterschiedlicher Frequenzen und Amplituden. Die Amplitude des Cosinus-Signales ist gleich der Amplitude des Sinus-Signales (kann geringfügig abweichen aber korrigiert werden). Das Transformieren erfolgt meist synthetisch, z.B. in digitalen Signal Prozessoren. Die Hilbert-Transformation wird verwendet, wenn man Sinus-Signal und Cosinus-Signal benötigt aber nur das Sinus-Signal vorliegt. Beide Signale (sin(...) und cos(...)) zusammen entsprechen einer Folge komplexer Zahlen. Damit kann man multiplikativ mischen ohne Spiegelfrequenz. Liegen beide Faktoren der Mischung als komplexe Zahlen vor, kann man jedes Glied der einen Zahl mit jedem Glied der anderen Zahl multiplizieren unter Beachtung der komplexen Einheit "j". Falls man sich dabei beide Faktoren jedoch in der exp( j * omega * t ) Schreibweise denkt, so multipliziert man statt dessen Potenzen, indem man die Exponenten addiert. Für eine Berechnung braucht man 4 Multiplikationen, was entweder digital erfolgen kann oder im analogen Fall vier Mischer (z.B. Ringmischer oder Gilbertzellen) benötigt, wenn man das ganze Ergebnis braucht. Der Transformationskern ist ein Array aus Zahlen deren Werte in der Mitte des Arrays groß sind und zum Rand hin abnehmen.
Weitere Literatur zu Hilbert
- Schüssler / Steffen "Halfband Filters and Hilbert Transformers"
Irgendwo im Web hatte ich den vollständigen Artikel als PDF gefunden, leider die Adresse nicht notiert, Google findet nur kostenpflichtige Downloads. - Dutta / Kumar On Digital Differentiators, Hilbert Transformers, and Half-Band Low-Pass Filters
dank Schrifterkennungsprogramm leicht lädiert - Miroslav Lutovac / Ljiljana Milic Half-band IIR Filter Design Using Matlab, weitere Artikel der Autoren
- Göckler / Damjanovic A Family of Efficient Complex Halfband Filters
ATmega-Programm Hilbert-Transformer ( fast fertig, schwingt leider)
Da der Adressenbereich des ATmega nicht groß genug ist, wird die Tabelle im SRAM in zwei Hälften geteilt.
;***************************************************************************
;* Hilbert transformer with ATmega48P, 90 degree broadband phase shifter *
;* 15 MHz xtal, input ADC0, PWM-output OCR1a/b, test output PD0 *
;* Christoph Kessler 2008 db1uq_at_t-online_dot_de *
;***************************************************************************
.nolist
.include "m48pdef.inc"
.list
;***************************************************************************
;* register 0-15 (no "immediate"-operations possible):
;***************************************************************************
.def mult_l = r0 ; multiplier result
.def mult_h = r1 ; multiplier result
.def zero = r2 ; zero register (used to add carry flag)
.def savsrg = r3 ; save status register during interrupt routine
.def reg04 = r4 ; free
.def reg05 = r5 ; free
.def reg06 = r6 ; free
.def reg07 = r7 ; free
.def reg08 = r8 ; free
.def reg09 = r9 ; free
.def reg10 = r10 ; free
.def reg11 = r11 ; free
.def reg12 = r12 ; free
.def accu0 = r13 ; Accumulator - 32bit for Interrupt routine
.def accu1 = r14 ; Accumulator - 32bit for Interrupt routine
.def accu2 = r15 ; Accumulator - 32bit for Interrupt routine
;***************************************************************************
;* register 16-23 ("immediate"-operations possible):
;***************************************************************************
.def accu3 = r16 ; Accumulator - 32bit for Interrupt routine
.def reg17 = r17 ; free
.def reg18 = r18 ; free
.def reg19 = r19 ; free
.def datal = r20 ; Data samples mul register
.def datah = r21 ; for Interrupt routine
.def coefl = r22 ; Filter coefficient mul register
.def coefh = r23 ; for Interrupt routine
;***************************************************************************
;* register 24-31 (16Bit-registers)
;***************************************************************************
.def tmp1 = r24 ; general temporary register
.def tmp2 = r25 ; general temporary register
; XL = r26 ; free
; XH = r27 ; free
; YL = r28 ; used by Interrupt routine
; YH = r29 ; used by Interrupt routine
; ZL = r30 ; init routine only, free for main program
; ZH = r31 ; init routine only, free for main program
;*************************************************************************
;* constants :
;*************************************************************************
;1st table:
;"allpass"0:
.equ x10 = 0
; allpass 2:
.equ x12 = 2
.equ x22 = 4
.equ y02 = 6
.equ y12 = 8
.equ y22 = 10
; allpass 4:
.equ x14 = 12
.equ x24 = 14
.equ y04 = 16
.equ y14 = 18
.equ y24 = 20
; allpass 6:
.equ x16 = 22
.equ x26 = 24
.equ y06 = 26
.equ y16 = 28
.equ y26 = 30
; allpass 8:
.equ x18 = 32
.equ x28 = 34
.equ y08 = 36
.equ y18 = 38
.equ y28 = 40
.equ k2 = 42
.equ k4 = 44
.equ k6 = 46
.equ k8 = 48
;2nd table:
.equ k1 = 0
.equ k3 = 2
.equ k5 = 4
.equ k7 = 6
; allpass 1:
.equ x11 = 8
.equ x21 = 10
.equ y01 = 12
.equ y11 = 14
.equ y21 = 16
; allpass 3:
.equ x13 = 18
.equ x23 = 20
.equ y03 = 22
.equ y13 = 24
.equ y23 = 26
; allpass 5:
.equ x15 = 28
.equ x25 = 30
.equ y05 = 32
.equ y15 = 34
.equ y25 = 36
; allpass 7:
.equ x17 = 38
.equ x27 = 40
.equ y07 = 42
.equ y17 = 44
.equ y27 = 46
;*****************************************************
;* Macros
;*****************************************************
.MACRO load_node
ldd datal,Y+@0 ; Load low byte of node
ldd datah,Y+@0+1 ; Load high byte of node
.ENDMACRO
.MACRO update_node
std Y+@0,datal ; Store low byte of node
std Y+@0+1,datah ; Store high byte of node
.ENDMACRO
.MACRO add_node
ldd coefl,Y+@0 ; Load 2nd node low
ldd coefh,Y+@0+1 ; Load 2nd node high
add datal,coefl ; Add low bytes
adc datah,coefh ; Add with carry high bytes
.ENDMACRO
.MACRO mult_32
ldd coefl,Y+@0 ; Load low byte of coefficient
ldd coefh,Y+@0+1 ; Load high byte of coefficient
muls coefh,datah ; Signed multiply, coefficient high byte and data high byte
mov accu2,mult_l ; Copy result word into accumulator byte 2:3
mov accu3,mult_h ; Copy result word into accumulator byte 2:3
mul coefl,datal ; Unsigned multiply, coefficient low byte and data low byte
mov accu0,mult_l ; Copy result word into accumulator byte 2:3
mov accu1,mult_h ; Copy result word into accumulator byte 2:3
mulsu coefh,datal ; Signed-unsigned multiply, coefficient high byte and data low byte
sbc accu3,zero ; Sign extention
add accu1,mult_l ; Add low byte of result to accumulator byte 1
adc accu2,mult_h ; Add with carry high byte of result to accumulator byte 2
adc accu3,zero ; Add carry to accumulator byte 3
mulsu datah,coefl ; Signed-unsigned multiply, data high byte and coefficient low byte
sbc accu3,zero ; Sign extention
add accu1,mult_l ; Add low byte of result to accumulator byte 1
adc accu2,mult_h ; Add with carry high byte of result to accumulator byte 2
adc accu3,zero ; Add carry to accumulator byte 3
.ENDMACRO
.MACRO subtr_node
ldd datal,Y+@0 ; Load 2nd node low
ldd datah,Y+@0+1 ; Load 2nd node high
sub accu0,datal ; Subtract low byte
sbc accu1,datah ; Subtract with carry high byte
sbc accu2,zero ;
sbc accu3,zero ;
.ENDMACRO
.MACRO limit_store
cpi accu3,$40 ; accu < $40000000 ?
brlo NoLimit1 ;
cpi accu3,-$40 ; accu >= -$40000000 ?
brsh NoLimit1 ;
clr accu2 ; accu2 = $00
cpi accu3,0 ;
brge PosLim1 ;
ldi accu3,$80 ; accu3 = $80
rjmp Limit1 ;
PosLim1:
ldi accu3,$7F ; accu3 = $7F
com accu2 ; accu2 = $FF
rjmp Limit1 ;
NoLimit1:
lsl accu1 ; Scaling to gain factor 2^16
rol accu2 ;
rol accu3 ;
Limit1:
std Y+@0,accu2 ;
std Y+@0+1,accu3 ;
.ENDMACRO
.LISTMAC
;*************************************************************************
;* reset/interrupt-vectors:
;*************************************************************************
.cseg
rjmp Initial ; after RESET to main program
reti ; External Interrupt Request 0
reti ; External Interrupt Request 1
reti ; Pin Change Interrupt Request 0
reti ; Pin Change Interrupt Request 1
reti ; Pin Change Interrupt Request 2
reti ; Watchdog Time-out Interrupt
reti ; Timer/Counter2 Compare Match A
reti ; Timer/Counter2 Compare Match B
reti ; Timer/Counter2 Overflow
reti ; Timer/Counter1 Capture Event
reti ; Timer/Counter1 Compare Match A
reti ; Timer/Counter1 Compare Match B
reti ; Timer/Counter1 Overflow
reti ; Timer/Counter0 Compare Match A
reti ; Timer/Counter0 Compare Match B
reti ; Timer/Counter0 Overflow
reti ; SPI Serial Transfer Complete
reti ; USART0, Rx Complete
reti ; USART0 Data register Empty
reti ; USART0, Tx Complete
rjmp ADCint ; ADC Conversion Complete
reti ; EEPROM Ready
reti ; 2-wire Serial Interface
reti ; Store Program Memory Read
;*************************************************************************
;* after reset: initialise stack,ports
;*************************************************************************
Initial:
ldi tmp1,Low(RAMEND)
out SPL,tmp1 ;
ldi tmp1,High(RAMEND)
out SPH,tmp1 ; stack initialised
clr zero ; always zero
ldi tmp1,$FF ;
out PortB,tmp1 ; PortB = % 1111 1111
out PortC,zero ; PortC = % 0000 0000
out PortD,tmp1 ; PortD = % 1111 1111
out DDRB,tmp1 ; PortB direction = % 1111 1111
out DDRC,zero ; PortC direction = % 0000 0000
out DDRD,tmp1 ; PortD direction = % 1111 1111
ldi tmp1,$A1 ; pos. outputs, fast PWM 8Bit
sts TCCR1A,tmp1 ;
ldi tmp1,$09 ; fast PWM 8Bit, clk/1 (no prescaling)
sts TCCR1B,tmp1 ;
sts OCR1AH,zero ;
sts OCR1AL,zero ;
sts OCR1BH,zero ;
sts OCR1BL,zero ;
ldi tmp1,$40 ; Ref=Vcc, right-adj, ADC0=input
sts ADMUX,tmp1 ;
ldi tmp1,$EE ; Start,Auto, enable Int, Clk/64
; ldi tmp1,$EF ; Start,Auto, enable Int, Clk/128
sts ADCSRA,tmp1 ;
ldi tmp1,$00 ; free running
sts ADCSRB,tmp1 ;
ldi tmp1,$01 ; disable ADC0 dig.inp (optional)
sts DIDR0,tmp1 ;
ldi ZL,low(CoTblF<<1) ; move filter coefficents
ldi ZH,high(CoTblF<<1) ; from program-flash
ldi YL,low(CoTblS) ; to SRAM
ldi YH,high(CoTblS) ;
ldi tmp1,16 ; count 8 * 2-Byte coefficients
TbLoop:
lpm tmp2,Z+ ; fetch 1 byte from coefficient table
st Y+,tmp2 ; copy coefficient to Sram, increment Y
dec tmp1
brne TbLoop
ldi YL,low(DatTbl1) ; load SRAM-Pointer for Interrupt routine
ldi YH,high(DatTbl1) ;
sei ; enable interrupts
;*************************************************************************
;* Main program:
;*************************************************************************
Endless:
rjmp Endless ;
;*************************************************************************
;* ADC-Interrupt routine: compute filter and update PWM output
;*************************************************************************
ADCint:
sbi PortD,0 ; just to measure INT-Time
in savsrg,SREG ; save status register
;*************************************************************************
; allpass 2
load_node x10 ;
add_node y22 ; y22 +---+ y12 +---+
mult_32 k2 ; o--<-|1/z|<-o--|1/z|<---+
subtr_node x22 ; | +---+ +---+ |
limit_store y02 ; v |
load_node x12 ; x10 +---+ +---+ +---+ |
update_node x22 ; o-->| + |-->|*K2|--->| - |--->o--->
load_node x10 ; | +---+ +---+ + +---+ y02
update_node x12 ; | - A
lds datal,ADCL ; | +---+ +---+ |
lds datah,ADCH ; +----|1/z|--o->|1/z|->-o
dec datah ; | +---+ x12 +---+ x22
dec datah ; |
lsl datal ; +-----------+
rol datah ; +---+ |
lsl datal ; ADC >--|1/z|--+
rol datah ; +---+
lsl datal ;
rol datah ;
lsl datal ; convert 10 bit unsigned
rol datah ; to 15 Bit signed
lsl datal ; $03FF -> $01FF -> $3FE0
rol datah ; $0000 -> $FE00 -> $C000
lsl datal ;
rol datah ;
update_node x10 ; save new sample for 2nd allpass-chain
load_node y12 ;
update_node y22 ;
load_node y02 ;
update_node y12 ;
; allpass 4
add_node y24 ;
mult_32 k4 ; y24 +---+ y14 +---+
subtr_node x24 ; o--<-|1/z|<-o--|1/z|<---+
limit_store y04 ; | +---+ +---+ |
load_node x14 ; v |
update_node x24 ; y02 +---+ +---+ +---+ |
load_node y02 ; ->o-->| + |-->|*K4|--->| - |--->o--->
update_node x14 ; | +---+ +---+ + +---+ y04
load_node y14 ; | - A
update_node y24 ; | +---+ +---+ |
load_node y04 ; +----|1/z|--o->|1/z|->-o
update_node y14 ; +---+ x14 +---+ x24
; allpass 6
add_node y26 ;
mult_32 k6 ; y26 +---+ y16 +---+
subtr_node x26 ; o--<-|1/z|<-o--|1/z|<---+
limit_store y06 ; | +---+ +---+ |
load_node x16 ; v |
update_node x26 ; y04 +---+ +---+ +---+ |
load_node y04 ; ->o-->| + |-->|*K6|--->| - |--->o--->
update_node x16 ; | +---+ +---+ + +---+ y06
load_node y16 ; | - A
update_node y26 ; | +---+ +---+ |
load_node y06 ; +----|1/z|--o->|1/z|->-o
update_node y16 ; +---+ x16 +---+ x26
; allpass 8
add_node y28 ;
mult_32 k8 ; y28 +---+ y18 +---+
subtr_node x28 ; o--<-|1/z|<-o--|1/z|<---+
limit_store y08 ; | +---+ +---+ |
load_node x18 ; v |
update_node x28 ; y06 +---+ +---+ +---+ |
load_node y06 ; ->o-->| + |-->|*K8|--->| - |--->o--->
update_node x18 ; | +---+ +---+ + +---+ y08
load_node y18 ; | - A
update_node y28 ; | +---+ +---+ |
load_node y08 ; +----|1/z|--o->|1/z|->-o
update_node y18 ; +---+ x18 +---+ x28
load_node x10 ;
ldi YL,Low(DatTbl2) ;
; allpass 1
add_node y21 ;
mult_32 k1 ; y21 +---+ y11 +---+
subtr_node x21 ; o--<-|1/z|<-o--|1/z|<---+
limit_store y01 ; | +---+ +---+ |
load_node x11 ; v |
update_node x21 ; x10 +---+ +---+ +---+ |
load_node x10 ; ->o-->| + |-->|*K1|--->| - |--->o--->
update_node x11 ; | +---+ +---+ + +---+ y01
load_node y11 ; | - A
update_node y21 ; | +---+ +---+ |
load_node y01 ; +----|1/z|--o->|1/z|->-o
update_node y11 ; +---+ x11 +---+ x21
; allpass 3
add_node y23 ;
mult_32 k3 ; y23 +---+ y13 +---+
subtr_node x23 ; o--<-|1/z|<-o--|1/z|<---+
limit_store y03 ; | +---+ +---+ |
load_node x13 ; v |
update_node x23 ; y01 +---+ +---+ +---+ |
load_node y01 ; ->o-->| + |-->|*K3|--->| - |--->o--->
update_node x13 ; | +---+ +---+ + +---+ y03
load_node y13 ; | - A
update_node y23 ; | +---+ +---+ |
load_node y03 ; +----|1/z|--o->|1/z|->-o
update_node y13 ; +---+ x13 +---+ x23
; allpass 5
add_node y25 ;
mult_32 k5 ; y25 +---+ y15 +---+
subtr_node x25 ; o--<-|1/z|<-o--|1/z|<---+
limit_store y05 ; | +---+ +---+ |
load_node x15 ; v |
update_node x25 ; y03 +---+ +---+ +---+ |
load_node y03 ; ->o-->| + |-->|*K5|--->| - |--->o--->
update_node x15 ; | +---+ +---+ + +---+ y05
load_node y15 ; | - A
update_node y25 ; | +---+ +---+ |
load_node y05 ; +----|1/z|--o->|1/z|->-o
update_node y15 ; +---+ x15 +---+ x25
; allpass 7
add_node y27 ;
mult_32 k7 ; y27 +---+ y17 +---+
subtr_node x27 ; o--<-|1/z|<-o--|1/z|<---+
limit_store y07 ; | +---+ +---+ |
load_node x17 ; v |
update_node x27 ; y05 +---+ +---+ +---+ |
load_node y05 ; ->o-->| + |-->|*K7|--->| - |--->o--->
update_node x17 ; | +---+ +---+ + +---+ y07
load_node y17 ; | - A
update_node y27 ; | +---+ +---+ |
load_node y07 ; +----|1/z|--o->|1/z|->-o
update_node y17 ; +---+ x17 +---+ x27
;*************************************************************************
;* PWM - D/A-output
;*************************************************************************
; output y07 to PWM-DAC
;test: output y01
ldd accu3, Y+y01+1 ;
;
subi accu3,$80 ; signed to unsigned $8000 ->$0000, $7FFF ->$FFFF
sts OCR1AH,zero ;
sts OCR1AL,accu3 ; fast PWM 8 bit y07 output to OCR1A
ldi YL,Low(DatTbl1) ; back to 1st data table
; output y08 to PWM-DAC
; load_node y08 ; load y08
; test outpt y02
load_node y02 ; load y02
;
subi datah,$80 ; signed to unsigned $8000 ->$0000, $7FFF ->$FFFF
sts OCR1BH,zero ;
sts OCR1BL,accu3 ; fast PWM 8 bit y08 output to OCR1B
cbi PortD,0 ; just to measure INT-Time
out SREG,savsrg ; restore status register
reti ;
;*************************************************************************
;* coefficient table in flash memory
;*************************************************************************
CoTblF:
.dw 15709 ; k2 *32768 (0,4794008655888)
.dw 28712 ; k4 *32768 (0,8762184935393)
.dw 32001 ; k6 *32768 (0,9765975895082)
.dw 32686 ; k8 *32768 (0,9974992559356)
.dw 5301 ; k1 *32768 (0,1617584983677)
.dw 24020 ; k3 *32768 (0,7330289323415)
.dw 30977 ; k5 *32768 (0,9453497003291)
.dw 32460 ; k7 *32768 (0,9905991566845)
;*************************************************************************
;* data in SRAM
;*************************************************************************
.dseg
.org $0100
DatTbl1:
; "allpass" 0
.dw $0000 ; x10
; allpass 2
.dw $0000 ; x12
.dw $0000 ; x22
.dw $0000 ; y02
.dw $0000 ; y12
.dw $0000 ; y22
; allpass 4
.dw $0000 ; x14
.dw $0000 ; x24
.dw $0000 ; y04
.dw $0000 ; y14
.dw $0000 ; y24
; allpass 6
.dw $0000 ; x16
.dw $0000 ; x26
.dw $0000 ; y06
.dw $0000 ; y16
.dw $0000 ; y26
; allpass 8
.dw $0000 ; x18
.dw $0000 ; x28
.dw $0000 ; y08
.dw $0000 ; y18
.dw $0000 ; y28
CoTblS:
.dw $0000 ; k2
.dw $0000 ; k4
.dw $0000 ; k6
.dw $0000 ; k8
DatTbl2:
.dw $0000 ; k1
.dw $0000 ; k3
.dw $0000 ; k5
.dw $0000 ; k7
; allpass 1
.dw $0000 ; x11
.dw $0000 ; x21
.dw $0000 ; y01
.dw $0000 ; y11
.dw $0000 ; y21
; allpass 3
.dw $0000 ; x13
.dw $0000 ; x23
.dw $0000 ; y03
.dw $0000 ; y13
.dw $0000 ; y23
; allpass 5
.dw $0000 ; x15
.dw $0000 ; x25
.dw $0000 ; y05
.dw $0000 ; y15
.dw $0000 ; y25
; allpass 7
.dw $0000 ; x17
.dw $0000 ; x27
.dw $0000 ; y07
.dw $0000 ; y17
.dw $0000 ; y27
;*************************************************************************