Modellierung analoger Schaltungen
Dieser Artikel untersucht die Möglichkeit, reale analoge Bauteile und Schaltungen mathematisch nachzubilden und simulieren zu können, um z.B. ihr Verhalten zu überwachen und voraussagen zu können. Es wird damit auch dargestellt, ob und inwieweit es möglich ist, analoge Schaltungen mit digitalen Systemen zu ersetzen, wie das z.B. bei Filtern und Signalerzeugern der Fall ist.
Vorbemerkung
Die Aufstellung ist ursprünglich für die Umsetzung in FPGAs mit einer damaligen Taktfrequenz von 50 MHz erstellt worden und wurde für diesen Artikel entsprechend skaliert. Sie gilt sinngemäß auch für Microcontroller und PC-Systeme. Dazu würde man die Betrachtung der Resourcen im FPGA ignorieren und nur die gefroderte Rechenleistung in Betracht ziehen. Diese müsste entsprechend der Möglichkeiten des jeweilgen DSPs oder der CPU interpretiert werden:
Für DSPs kann man diesbezüglich etwa 60% ... 80% Auslastung für die Berechnung ansetzen (Rest für Verwaltung und zusätzliche Speicherzugriffe) - aufgrund der besseren Arithmetik heutiger DSPs etwa 150% bis 200% der Rechenleistung - insbesondere bei genauen Anforderungen. Der hier beispielhaft angenommene FPGA mit 200 MHz entspräche im Bezug auf eine typische Multiplikation und Speicheropration in etwa einem 150MHz Audio DSP mit 24 Bit, bzw. 120MHz DSP mit 32 Bit.
Für aktuelle CPUs kann man etwa 40% ... 60% der Auslastung - und aufgrund der Arithmetik etwa 150% ... 250% der Rechenleistung pro Takt annehmen - inbegriffen der Tatsache, dass bei den Schritten unten auch nicht-arithmetische Aktionen mitgerechnet werden, bei denen die CPU keine Vorteile hat. Ein durchschnittlich ausgelasteter 4-Kern-Intel7 mit 3GHz kommt so praktisch auf das 10-fache bis 30-fache der Leistung eines FPGAs für eine Operation. Bei DSPs und CPUs müssen dann aber noch Speicher- und externe RAM-Zyklen berücksichtigt werden, die die Performance um z.T. 25% bis 75% senken. Ein direkter Vergleich zwischen FPGA und einer solchen CPU wies für eine Klangsyntheseschaltung konkret einen Faktor 8.2 für die CPU aus. Da die CPU aber nur begrenzt parallelisieren kann, sinkt der Faktor für die Werte in den letzten beiden Tabellen, welche die Parallelisierung mit pipelining untersuchen, schnell ab.
Wesentlich bei FPGAs ist die Berücksichtigung der gleichzeitig verfügbaren Resourcen. Typische FPGAs hatten zum Zeitpunkt der Artikelerstellung meist nur 20-40 Multipliziereinheiten. Auch die Anzahl der physisch parallen Speicherblöcke war begrenzt. Mit einem aktuellen FPGA unter 100€,- sind inzwischen hunderte Multiplizierer und Speicherblöcke verfügbar. Damit sind sehr rasch Rechen- und Daten-Bandbreiten zu erzielen, welche auch 16-Kern-CPU um ein mehrfaches übertreffen. Eine ähnliche Betrachtung lässt sich auch für Grafikkarten (GPU-processing) machen.
Im Folgenden wird einzeln untersucht, welche Performance-Anforderungen an den FPGA / die CPU bestehen und wie diese zustande kommen:
Rechenbedarf für Modelle
Die folgende Tabelle zeigt den Bedarf an Rechen- und Prozessschritten für unterschiedliche Bauelemente je nach Komplexität des gewählten Modells:
Tabelle 1
| Modell | Gleichungen | Parameter | Berechnungen | Operationen | Schritte |
|---|---|---|---|---|---|
| Transistor 3D - physisch | 31 | 73 | 3700 | 4700 | 13200 |
| Transistor hSpice | 17 | 32 | 890 | 1190 | 2000 |
| pSPice | 9 | 19 | 232 | 304 | 427 |
| BiPol - KleinSignal | 5 | 7 | 64 | 89 | 121 |
| BiPol - Lineariarisiert | 3 | 5 | 24 | 33 | 46 |
| Theoretischer Transistor | 1 | 9 | 11 | 12 | 18 |
| Widerstand 3D HF | 9 | 21 | 225 | 306 | 430 |
| Widerstand 2D LF | 5 | 12 | 69 | 94 | 128 |
| Widerstand pSpice | 3 | 5 | 24 | 33 | 46 |
| Widerstand - Linearisiert | 1 | 3 | 5 | 6 | 10 |
| Theoretischer Widerstand | 1 | 1 | 3 | 4 | 8 |
| Kondensator 3D HF | 17 | 37 | 904 | 1193 | 2011 |
| Kondensator 2D LF | 9 | 18 | 222 | 303 | 426 |
| Kondensator pSpice | 5 | 7 | 64 | 89 | 121 |
| Kondensator - Linearisiert | 2 | 3 | 11 | 15 | 22 |
| Theoretischer Kondensator | 1 | 1 | 3 | 4 | 8 |
| Spule 3D HF - freq | 23 | 45 | 1819 | 2350 | 4825 |
| Spule 2D LF - freq | 16 | 31 | 783 | 1040 | 1710 |
| Spule pSpice | 7 | 11 | 129 | 178 | 244 |
| Spule - Linearisiert | 3 | 6 | 25 | 34 | 47 |
| Theoretische Spule | 1 | 3 | 5 | 6 | 10 |
Anmerkungen
Der 3D-Transistor ist eine Sammlung von Formeln, welche sich aus der Analyse eines räumlich ausgedehnten Gebildes im Silizium ergibt, so wie es im physikalischen Simulator zur Chipherstellung verwendet wird. Das Spice-Modell ist der angepasste C-Code des Modells aus Cadence, bzw das Equivalent. Das Modell unter "BiPol" ist das klassische Kleinsignalersatzschaltbild und - verhalten eines Transistors gemäß Möschwitzer / Lunze und Titze -Schenk. Der theoretische Transistor besteht aus einer Formel mit Teillinearisierungen (und entsprechenden Abweichungen). Für MOS-Fet und BiPolar wird dieselbe Abschätzung verwendet, wobei die Charakterisierung des MosFet aufwändiger ist und den BiPo nach oben abschätzt.
Erwartungsgemäß haben umfangreichere Modelle mehr Formeln, Parameter und auch Rechentiefe. Bei Widerstand und Kondensator werden mitunter auch Temperatur, Induktivität und Streuung berücksichtigt, die sich aus realen Bauteilgehäuseformen ergeben, Bei den höheren Kondensator-Modellen sind auch die geringe Nichtlinearität des Dielektrikums und die Leckströme abgebildet.
Die Spule ist besonders trickreich, wegen der Streufelder im 3D-Fall und der "seltsamen" Frequenzabhängigkeit schon im im 2D-Fall. Das Magnetmodell ist jenes nach Jiles-Atherton ("Spice"), das 2D ein modifiziertes Carpenter-Modell von mir, das komplett in VHDL erstellt wurde und in mehreren Ausbaustufen verwendet wird.
Die Berechnungsformeln wurden u.a. in MATLAB umgesetzt und in lineares VHDL gewandelt. Daraus ergeben sich je nach Komplexität des Modells die anwendungsabhängige Anzahl von Rechenschritten. Der Bedarf ist als grober Anhaltspunkt zu sehen und kann stärker variieren.
Bei der Betrachtung der notwendigen Rechenschritte für CPUs ist der Wert entsprechend der Möglichkeiten der Arithmetik und der Rechenanforderungen gfs ein anderer. Auch sind die Besonderheiten von PCs in Betracht zu ziehen. Daher ergeben sich bei einer virtuellen Simulation in MATLAB oder pSPice sehr viel geringere Werte, als die Tabelle suggeriert.
Bauelementebedarf
Die nachfolgende Tabelle zeigt exemplarisch den Bedarf an typischen Bauelementen für unterschiedliche ausgewählte Analogschaltungen:
Tabelle 2
| Anwendung | Halbleiter | Widerstände | Kondensatoren | Spulen | I,U,B,H,N |
|---|---|---|---|---|---|
| Ein-Transistor-Verstärker | 1 | 4 | 2 | 0 | 8 |
| Gegentaktverstärker | 4 | 6 | 4 | 2 | 17 |
| AB-HIFI-Verstärker | 14 | 15 | 11 | 4 | 45 |
| Operationsverstärker | 18 | 32 | 6 | 0 | 57 |
| HIFI-Amp mit Preamp | 27 | 42 | 26 | 8 | 104 |
| Monophoner Analogsynthesizer | 155 | 235 | 130 | 36 | 557 |
| 8-fach polyphoner Synthesizer mit Filtern | 1.085 | 1.450 | 850 | 240 | 3.626 |
Anmerkungen
Für die Abschätzung des grundsätzlichen Rechenbedarfs werden Beispielschaltungen herangezogen und die durchschnittliche Zahl sowie Art der Bauelemente bestimmt. Dabei werden 2 Dioden wie 1 Transistor gerechnet, ein Darlington-Transistor als 2 Transistoren. Mit I,U,B,H und N sind Spannungsquellen, Stromquellen sowie B- und H-Felder gemeint, die mit simuliert werden sollen. Eingeschlossen darin sind auch Störungen und das Rauschen auf Leitungen. Z.B. sind dies Rauschquellen beim Widerstand und induzierte Ströme, aber auch Rückwirkungen von Feldern. Laut Tabelle handelt es sich um scheinbar viele Parameter, welche aber in der realen Rechnung einen überschaubaren Rechenaufwand verursachen, da sie nur additiv wirken. Dennoch sind sie für das Ergebnis wichtig. Rauschen fördert z.B. die Konvergenz von Iterationen und hilft, Ungenauigkeiten bei den Rechnungen zu überwinden.
Schaltungskomplexität beim Beispiel Hochpass
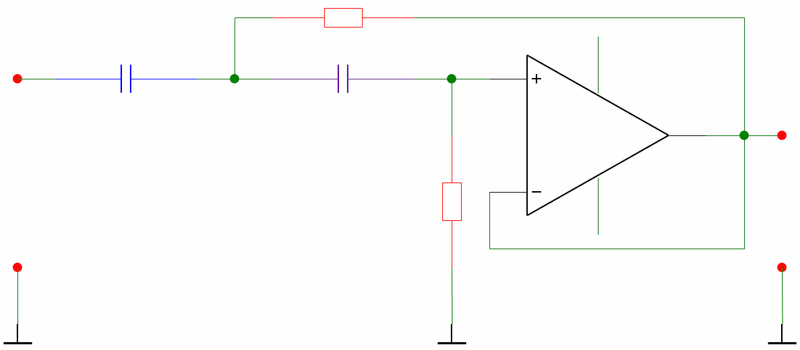
Maßgeblich für die Menge der zu simulierenden Bauelemente ist hier bereits der Anspruch an die Genauigkeit: Je genauer der HF-Anteil einer Schaltung berechnet werden soll, desto mehr kommen Felder, Streuinduktivitäten und die Ausgestaltung des PCBs ins Spiel. Die nachfolgenden Zeichnungen zeigen beispielhaft 2 Simulationsansätze für eine Tiefpassschaltung.
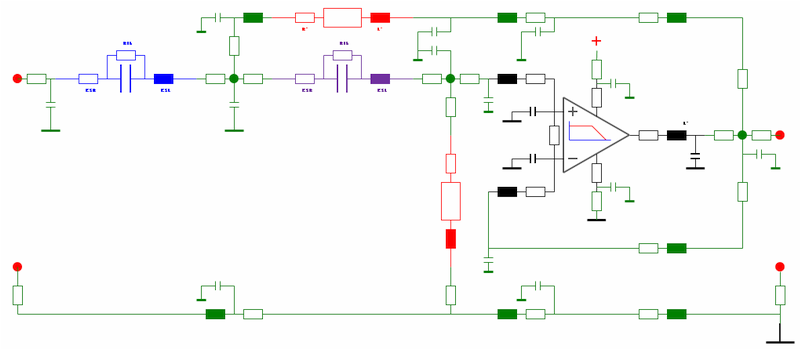
In der ersten kommen nur einfache theoretische Gleichungen zur Anwendung, darunter ein vollständig linearer Ansatz für den OPV. Der Ansatz führt zu einer geringen Zahl von Gleichungen und entsprechend schnellen Berechnung. In der unteren Zeichnung sind zusätzliche Bauelemente eingefügt, die helfen, das reale Verhalten besser nachzubilden. Dies betrifft neben den Komponenten (Eingangswiderstände und - kapazitäten) auch den Einfluss der konkreten Leiterbahnführung.
Diese Schaltung ist zwar auch noch signifikant von der Realität entfernt, da der OP nach wie vor bis auf eine Ausgangsdämpfung linear modelliert wurde, dennoch war es möglich, das Verhalten bis etwa 100kHz für kleine Signale weitgehend exakt nachzustellen, was für Audiosimulationen taugen würde. Darüber hinaus kommt zunehmend der OP und seine limitierte Bandbreite ins Spiel. Für echte HF-Simulationen müssten weitere Effekte Berücksichtigung finden.
Rechenzeitbedarf
Die nachfolgende Tabelle zeigt den Bedarf an Rechenschritten für die gewählten Schaltungen je nach Modell:
Tabelle 3
| Anwendung | Theoretisch | Linear | pSpice | 2D-Modell | 3D-Modell |
|---|---|---|---|---|---|
| Ein-Transistor-Verstärker | 82 | 146 | 563 | 1.810 | 19.020 |
| Gegentaktverstärker | 206 | 460 | 1.765 | 7.615 | 73.000 |
| AB-HIFI-Verstärker | 590 | 315 | 4.780 | 19.475 | 233.500 |
| Operationsverstärker | 742 | 1.395 | 4.490 | 14.450 | 264.400 |
| HIFI-Amp mit Preamp | 1.118 | 2.820 | 10.500 | 41.780 | 266.850 |
| Monophoner Analogsynthesizer | 7.184 | 15.165 | 55.190 | 213.950 | 2.590.700 |
| 8-fach polyphoner Synthesizer mit Filtern | 47.580 | 101.600 | 366.700 | 1.426.400 | 17.870.000 |
Anmerkungen
Diese Tabelle ist effektiv das Ergebnis der Verknüpfung der beiden vorherigen Tabellen unter Anrechnung der Anzahl der beteiligten Bauelemente und dem offset zur Verwaltung von z.B. Stimulationsobjekten.
Erwartungsgemäß erfordern größere Schaltungen mit komplexeren Modellen überproportional immer mehr Rechenschritte, um einen einzelnen Rechnungsdurchlauf einer simulierten Zeiteinheit zu absolvieren. Bei umfangreichen Schaltungen entstehen zudem sehr viele Verbindungen, Schleifen und Einflüsse, welche den Rechenaufwand nach oben treiben. Der zuvor dargestellte Hochpass erforderte z.B. die 15-fache Zahl von Rechenschritten im Vergleich zum einfachen Modell und erreicht im Volumen bereits das Innere eines vollständigen OPs.
Es ist hier sicher schon einsichtig, dass die einfachen linearisierten Modelle kein Detailverhalten wiedergeben-, sondern im Rahmen von Simulationen nur das Prinzip der Funktion darstellen können. Alle Feinheiten, insbesondere die Abweichungen der realen Bauelemente vom Ideal, fehlen hier.
Maximale Iterationsfrequenz
Die nachfolgende Tabelle zeigt die Anzahl der möglichen Iterationen je Sekunde bei Abarbeitung der vollständigen analytischen Gleichungen mit dem angenommen 200MHz FPGA:
Tabelle 4
| Anwendung | Theoretisch | Linear | pSpice | 2D-Modell | 3D-Modell |
|---|---|---|---|---|---|
| Ein-Transistor-Verstärker | 2.500.000 | 1.400.000 | 355.000 | 110.000 | 10.500 |
| Gegentaktverstärker | 970.000 | 434.000 | 113.000 | 26.200 | 2.730 |
| AB-HIFI-Verstärker | 338.000 | 152.000 | 41.800 | 10.270 | 857 |
| Operationsverstärker | 269.000 | 143.000 | 44.500 | 13.840 | 756 |
| HIFI-Amp mit Preamp | 152.000 | 70.900 | 19.040 | 4.786 | 428 |
| Monophoner Analogsynthesizer | 27.840 | 13.200 | 3.624 | 934 | 77 |
| 8-fach polyphoner Synthesizer mit Filtern | 4.200 | 1.968 | 545 | 140 | 11 |
Anmerkungen
Unter der Annahme einer optimalen Ausnutzung des Chips und der typischen Auslastung der Fläche wie oben angesetzt, ergibt sich bei der Taktfrequenz eine maximale Anzahl von Durchläufen einer Iterations-Schleife, bis ein Ergebnis vorliegt. Diese entspricht der invertierten Latenz. Die Abschätzung zeigt, dass - die betreffende Hardware vorausgesetzt - es grundsätzlich möglich wäre, auch ein sehr kompliziertes Analogmodell mit immerhin 10Hz punktweise zu simulieren, was für Untersuchungen der Funktion im Vorfeld des Designs reichen würde.
Die hier inbegriffene Streuung beträgt etwa 50% ... 100% je nach individueller Konvergenz und Ausbau des FPGAs sowie Qualität der Umsetzung, d.h. ein Maximalmodell eines Analogsynthesizers oder einer Filterbank, wie unten rechts angenommen wurde, kann statt 100ms zwischen 50ms und 200ms pendeln. Die Größenordnung bleibt aber in diesem Bereich.
Oversampling
Die nachfolgende Tabelle zeigt den ungefähren Bedarf an Oversampling und die Anzahl der Iterationen, bis eine ausreichende Konvergenz und damit Genauigkeit bei numerischer Berechnung erzielt wird. Die Werte ergeben sich aus Erfahrung sowie aus der Grundbetrachtung der notwendigen Repräsentation von Oberwellen eines Signals bei z.B. Faltungsoperationen. Vor allem schlägt sich hier ein zunehmend schlechteres Konvergenzverhalten der Rechnung beim Finden der Lösungen für umfangreiche Schaltungen mit Energiespeichern wie Drosseln und verlustbehaftete Kondensatoren nieder.
Tabelle 5
| Anwendung | Theoretisch | Linear | pSpice | 2D-Modell | 3D-Modell |
|---|---|---|---|---|---|
| Ein-Transistor-Verstärker | 4 | 6 | 8 | 32 | 128 |
| Gegentaktverstärker | 6 | 9 | 12 | 48 | 192 |
| AB-HIFI-Verstärker | 8 | 12 | 16 | 64 | 256 |
| Operationsverstärker | 12 | 18 | 24 | 96 | 384 |
| HIFI-Amp mit Preamp | 16 | 24 | 32 | 128 | 512 |
| Monophoner Analogsynthesizer | 24 | 36 | 48 | 192 | 768 |
| 8-fach polyphoner Analogsynthesizer mit Filtern | 32 | 48 | 64 | 256 | 1024 |
Anmerkungen
Je nach Anwendung ist ein oversampling der Rechnung, eine Überhöhung der Taktfrequenz für numerische Rechnungen in Echtzeit und auch die gesteigerte Anzahl der echten Iterationen zu berücksichtigen. Dabei erfordern komplexere und umfangreichere Anwendungen für die letztlich gleiche Genauigkeit zunehmend mehr Iterationen. Zudem werden die Anforderungen an umfangreiche Schaltungen auch im Hinblick auf die Genauigkeit steigen. Daraus ergibt sich gewöhnlich ein ungefähr quadratisches Verhalten des Bedarfs mit wachsender Größe der Schaltung und des Modells. Gleichzeitig verläuft die Genauigkeit mit der Potenz der Anzahl der Iterationen, wächst also stärker, als linear. Damit ergibt sich ein mittleres Verhalten aus linearer Steigung und Potenzierung, was die Zahl der nötigen Iterationen / Takte angeht.
Die Tabelle zeigt Erfahrungs- und Schätzwerte, die entsprechend variieren können. Der beispielhaft angeführte Hochpass musste seinerzeit schon mit fast der 10-fachen Abtastrate / Feinheit der Simulationsschritte simuliert werden, um realitätsnahe Ergebnisse zu erhalten und das Verhalten im höheren kHz-Bereich zufriedenstellend abzubilden. Insgesamt erforderte es eine fast 100-fache Rechenzeit gegenüber dem einfachen Modell.
Resultierende Abtastfrequenz
Die nachfolgende Tabelle zeigt die aus den Vorbetrachtungen resultierende mögliche Anzahl der Abtastungen für die vollständigen Iterationen :
Tabelle 6
| Anwendung | Theoretisch | Linear | pSpice | 2D-Modell | 3D-Modell |
|---|---|---|---|---|---|
| Ein-Transistor-Verstärker | 610.000 | 228.000 | 44.400 | 3.459 | 82 |
| Gegentaktverstärker | 161.000 | 48.300 | 9.400 | 547 | 14 |
| AB-HIFI-Verstärker | 42.300 | 12.600 | 2.600 | 160 | 3 |
| Operationsverstärker | 22.400 | 7.900 | 1.850 | 143 | 2 |
| HIFI-Amp mit Preamp | 9.400 | 2.900 | 595 | 37 | 0,8 |
| Monophoner Analogsynthesizer | 1.160 | 367 | 75 | 5 | 0,1 |
| 8-fach polyphoner Analogsynthesizer mit Filtern | 131 | 41 | 9 | 0,5 | 0,011 |
Anmerkungen
Als Folge der nötigen Iterationen ergibt sich damit die Anzahl der echten Samples, die berechnet werden können und damit ein Hinweis auf die Echtzeitfähig der Anwendung. Um die jeweils erforderliche Genauigkeit und Frequenz zu ermitteln, muss die höchste auftretende Frequenz beachtet werden, welche für den Benutzer relevant ist, bzw. abgebildet werden soll. Diese ist maßgeblich für Authentizität der Berechnung und für z.B. Regelungen und Überwachungen wichtig. Für Temperaturen wären z.B. Raten von 10Hz und darunter möglicherweises ausreichend. Für Audiosignale wären mindestens 2x15kHz zu fordern. Mit Einschränkungen sind auch 5kHz ... 10kHz noch zulässig, wenn größere Abweichungen in den Höhen hakzeptiert werden können. Üblicherweise nehmen die Fehler in den Höhen mit jeder Oktave um 3...6db zu, was eine Abschätzung zulässt: Hat man z.B. bei einer angegebenen Frequenz eine definierte Präzision von 100dB THD Signalgüte erreicht und befindet sich genügend weit unterhalb der Eckfrequenz der Abtastrate, so kann man bei der 10-fachen Frequenz immerhin noch 80dB Güte erwarten und entscheiden, ob man man weniger überabtastet oder Iterationen früher abbricht.
An dieser Stelle sieht man bereits, dass realistischerweise nur sehr kleine und einfache Schaltungen in Echtzeit sinnvoll simuliert und überwacht werden können. Sobald komplexere Strukturen voliegen, müssen Vereinfachungen an den Gleichungen vorgenommen werden.
Benötigte Anzahl der FPGAs
Aus den Rechenanforderungen ergibt sich eine theoretische Anzahl von FPGAs, die zeitlich belegt werden. Fälle mit Zahlen unter 1.0 lassen die Berechnung mehrerer Einheiten in einem FPGA zu. Zahlen > 1 deuten hingegen darauf hin, dass es mehr Resourcen benötigt, um überhaupt 1 Schaltung berechnen zu können.
Tabelle 7
| Anwendung | Theoretisch | Linear | pSpice | 2D-Modell | 3D-Modell |
|---|---|---|---|---|---|
| Ein-Transistor-Verstärker | 0,1 | 0,1 | 0,3 | 1,0 | 11 |
| Gegentaktverstärker | 0,1 | 0,3 | 1,0 | 4,3 | 41 |
| AB-HIFI-Verstärker | 0,4 | 0,8 | 2,7 | 11 | 131 |
| Operationsverstärker | 0,4 | 0,8 | 2,6 | 8,2 | 149 |
| HIFI-Amp mit Preamp | 0,8 | 1,6 | 5,9 | 24 | 263 |
| Monophoner Analogsynthesizer | 4,1 | 8,6 | 31 | 120 | 1.458 |
| 8-fach polyphoner Analogsynthesizer mit Filtern | 27 | 57 | 206 | 803 | 10.050 |
Anmerkungen
Bei der Beurteilung, ob ein FPGA auch tatsächlich reicht, muss berücksichtigt werden, dass die Resourcen für einen sequenziellen Betrieb inklusive Verwaltung insgesamt reichen. In einigen Fällen der Teilauslastung ist dabei eine Teilparallelisierung effektiver und machbar. Bei Werten >1 reicht 1 FPGA aufgrund der gesamten Anforderungen nicht mehr aus, da die Rechnung von der Fläche her "zu lang" wird. Zwar gibt es einen schmalen Bereich, wo durch künstliche Sequenzialisierung (resource sharing) Resourcen gespart werden könnten, aber dies wird hier nicht betrachtet, da dann die Option des pipelinings entfiele, die im FPGA regelmäßig angewendet wird.
Maximale Performance
Die nachfolgende Tabelle zeigt die maximale Anzahl der parallelen Berechnungen bei totalem pipelining in angenommenden 16 FPGAs bei günstigster Verschaltung und Nutzung:
Tabelle 8
| Anwendung | Theoretisch | Linear | pSpice | 2D-Modell | 3D-Modell |
|---|---|---|---|---|---|
| Ein-Transistor-Verstärker | 215 | 145 | 46 | 15 | 1,5 |
| Gegentaktverstärker | 111 | 56 | 16 | 4 | 0,4 |
| AB-HIFI-Verstärker | 44 | 21 | 6 | 1,5 | 0,1 |
| Operationsverstärker | 36 | 20 | 6 | 2,0 | 0,1 |
| HIFI-Amp mit Preamp | 21 | 10 | 3 | 0,7 | 0,1 |
| Monophoner Analogsynthesizer | 4 | 2 | 0,5 | 0,1 | 0,01 |
| 8-fach polyphoner Synthesizer mit Filtern | 0,6 | 0,3 | 0,1 | 0,02 | 0,001 |
Anmerkungen
Bei einem CUBE-System aus 16 FPGAs ergibt sich die Möglichkeit, die Rechnung als solche aufgrund der benötigten Hardware sehr wohl zu implementieren und die Iteration zu schließen, gleichzeitig eine Anzahl von Situationen simultan zu berechnen und so den FPGA voll zu nutzen. Das ist insbesondere bei Monte-Carlo-Analysen vorteilhaft. Es ergibt sich dann eine rechnerisch maximale Anzahl gleichzeitiger Rechenkanäle. Eine Anzahl größer 1 gibt an, dass 16 FPGAs in Umfang und Tempo für die Anforderung ausreichen. Konstellationen <1 könnten zwar teilweise vom Platz her mehr, als 100% berechnen, erlauben es aber nicht, den Loop in Echtzeit schließen. Abhilfe schafft dann nur noch eine schnellere Technologie mit einer höheren Taktfrequenz.
Fazit
Wie man erwarten konnte, ist ein einzelnes Bauelement bei entsprechendem Aufwand leicht zu berechnen, wenn man nicht gerade ins 3D geht und alle erdenklichen parasitären Effekte mitberücksichtigen will. Aber bereits, wenn man eine kleinere Schaltung zusammensetzt, entstehen durch die Leitungsführung Effekte, die zu Verfälschungen der reinen Modelle führen. Je höher die Frequenz ist, die betrachtet wird, desto mehr Effekte müssen simuliert werden.
Nach meiner Einschätzung reicht für Audio die Modellierung auf Spice-Niveau gerade so aus, wenn man Leitungen und wichtige Störungen mit simuliert und diese als Einflüsse mit zusätzlichen Spannungen darstellt. Ansonsten laufen die Ergebnisse der Gleichungen rasch weg. Wichtig sind die Verluste bei Spulen und Kondensatoren, die oft nur unzureichend abgebildet werden.
Trotzdem ist eine einfache Transistorschaltung noch gut zu modellieren und zu überwachen. Das geht auch in Echtzeit und ist wie die Wettervorhersage für einen gewissen Zeitraum stimmig. Eine Echtzeitüberwachung muss dann durch Messungen unterstützt und immer wieder "eingefangen" werden. Eine Simulation läuft dann logischerweise weg und ist nur dem Prinzip nach exakt d.h. ein Schwingkreis, den man ausrechnet, kommt gfs zu einer leicht abweichenden Frequenz, schwingt aber weitgehend authentisch.
Sehr schwierig sind Spulen. Die Speicherwirkung des Feldes insbesondere die Streuung und Nichtlinearität bei magnetischen Werkstoffen ist eine Wissenschaft für sich. Ein weitgehend gut funktionierendes Ersatzmodell in VHDL, das ich entwickelt habe, füllte in der Realität schon einen halben FPGA. Mit den reduzierten Modellen darf man nicht erwarten, dass man Sättigungen und Oberwellen so hinbekommt, wie sie real auftreten. Wer also in seinem Analogschaltkreis eine Drossel mit Ferritkern hat, ist im Grunde schon "verloren".
Eine simple Drossel ist hingegen in etwa so genau zu simulieren wie ein Kondensator, wenn man die parasitären Effekte mit drin hat und kleine Ströme nutzt und nicht viel von Außen einstreut. Ansonsten liegt man im Bereich der Komplexität von Transistoren.