Spannungsteiler

Einleitung

Oft ist es notwendig, die Ausgangsspannung eines Sensors an den Eingangsspannungsbereich eines AD-Wandlers anzupassen. Ist die Ausgangsspannung größer als die Eingangsspannung, ist dies sehr einfach und kostengünstig mit einem Spannungsteiler machbar.

Einfacher Spannungsteiler

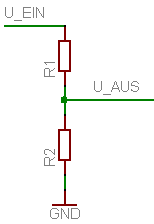
Die wohl einfachste Anwendung des Ohmschen Gesetzes ist der einfache Spannungsteiler. Dabei wird eine große Eingangsspannung linear in eine kleine Ausgangsspannung umgesetzt. Der mathematische Zusammenhang ist dabei

[math]\displaystyle{ U_\text{AUS} = U_\text{EIN} \cdot \frac{R_2}{R_1+R_2} }[/math].

Die Berechnung von [math]\displaystyle{ R_1 }[/math] und [math]\displaystyle{ R_2 }[/math] ist einfach. Es wird ein Wert für [math]\displaystyle{ R_1 }[/math] oder [math]\displaystyle{ R_2 }[/math] gewählt und die Formel nach [math]\displaystyle{ R_1 }[/math] bzw. [math]\displaystyle{ R_2 }[/math] umgestellt. Das soll hier beispielhaft geschehen.

[math]\displaystyle{ R_2 = R_1 \cdot \frac{U_\text{AUS}}{U_\text{EIN}-U_\text{AUS}} }[/math]

Für die Herleitung der Formel siehe den Wikipedia-Artikel zum Spannungsteiler.

Ein Windows-Programm, das den Spannungsteiler aus Widerständen der E12- oder E24-Reihe mit der niedrigsten Toleranz automatisch berechnet, findet sich unter elexs.de/kap2_4.htm. Online (mit JavaScript) geht dies unter gjlay.de/helferlein/spannungsteiler.html.

Spannungsteiler mit Biaskorrektur

Manche Spannungsteiler ziehen Strom, bzw. liefern einen konstanten Strom. Eine Möglichkeit besteht darin, die Widerstände niederohmig zu dimensionieren. Nachteil dieser Lösung ist die überproportional zunehmende Verlustleistung.

Alternativ kann man den Spannungsteiler mit Offset folgendermaßen berechnen:

[math]\displaystyle{ U_\text{AUS} = \frac{R_2 \cdot U_\text{EIN}}{R_1+R_2}-\frac{I_B}{\frac{1}{R_1}+\frac{1}{R_2}} }[/math]

Löst man die Gleichung nach [math]\displaystyle{ R_2 }[/math] auf, erhält man

[math]\displaystyle{ R_{2} = \frac{U_\text{AUS} \cdot R_1}{U_\text{EIN}-I_B \cdot R_1-U_\text{AUS}} }[/math].

Spannungsteiler mit Offset, passiv

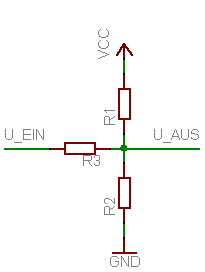
Um einiges komplizierter wird die Situation, wenn die Eingangsspannung mit einem Offset behaftet ist, oder wenn die Ausgangsspannung einen Offset haben soll. Hier kommt ein Spannungsteiler mit 3 Widerständen zum Einsatz. Die Berechnung der Widerstände [math]\displaystyle{ R_1 }[/math], [math]\displaystyle{ R_2 }[/math] und [math]\displaystyle{ R_3 }[/math] ist um einiges komplexer. Hier kann mit dem Überlagerungsprinzip (Superpositionsprinzip) gerechnet werden. Man erhält

[math]\displaystyle{ U_\text{AUS} = U_\text{EIN} \cdot \frac{\frac{R_1 \cdot R_2}{R_1+R_2}}{\frac{R_1 \cdot R_2}{R_1+R_2} + R_3} + V_\text{CC} \cdot \frac{\frac{R_3 \cdot R_2}{R_3+R_2}}{\frac{R_3 \cdot R_2}{R_3+R_2} + R_1} }[/math] und

[math]\displaystyle{ U_\text{EIN} = \left(U_\text{AUS} - V_\text{CC} \cdot \frac{\frac{R_3 \cdot R_2}{R_3+R_2}}{\frac{R_3 \cdot R_2}{R_3+R_2} + R_1}\right) \cdot \frac{\frac{R_1 \cdot R_2}{R_1+R_2} + R_3}{\frac{R_1 \cdot R_2}{R_1+R_2}} }[/math].

Mit

[math]\displaystyle{ R_a = R_1||R_2 = \frac{R_1 \cdot R_2}{R_1+R_2} }[/math] und

[math]\displaystyle{ R_b = R_3||R_2 = \frac{R_3 \cdot R_2}{R_3+R_2} }[/math]

lassen sich die Formeln etwas übersichtlicher schreiben:

[math]\displaystyle{ U_\text{AUS} = U_\text{EIN} \cdot \frac{R_a}{R_a + R_3} + V_\text{CC} \cdot \frac{R_b}{R_b + R_1} }[/math]

[math]\displaystyle{ U_\text{EIN} = \left(U_\text{AUS} - V_\text{CC} \cdot \frac{R_b}{R_b + R_1}\right) \cdot \frac{R_a + R_3}{R_a} }[/math]

Dieses Gleichungssystem ist unterbestimmt. Das heißt, dass es unendlich viele Lösungen gibt. Zur praktischen Anwendung muss man daher bei gegebenen Spannungswerten noch einen Widerstandswert wählen, zum Beispiel den von [math]\displaystyle{ R_2 }[/math], um die Werte der anderen Widerstände wie [math]\displaystyle{ R_1 }[/math] und [math]\displaystyle{ R_3 }[/math] bestimmen zu können.

Um die praktische Anwendung zu vereinfachen finden sich alle Formeln in einer Exceltabelle wieder. Die Nutzung ist praktisch selbsterklärend. Im oberen Teil trägt man alle gegebenen bzw. gewünschten Parameter ein, im Mittelteil erscheinen Zwischenergebnisse, die jedoch für die direkte Anwendung nicht von Bedeutung sind. Wichtig sind nur die Ergebnisse ganz unten mit den Werten für [math]\displaystyle{ R_1 }[/math] und [math]\displaystyle{ R_3 }[/math] sowie dem Eingangs- und Ausgangswiderstand des Spannungsteilers sowie die obere Grenzfrequenz.

Für die Anwendung ist es wichtig zu wissen, dass die Quelle, welche den Spannungsteiler speist, einen geringen Innenwiderstand haben muss, damit es nicht zu unakzeptablen Messfehlern kommt. „Pi mal Daumen“ gilt, dass der Innenwiderstand nur 1 % vom Eingangswiderstand des Spannungsteilers betragen darf, damit der Messfehler nicht größer als 1 % wird ([math]\displaystyle{ R_2 }[/math] möglichst groß wählen). Ist das nicht möglich, dann muss ein Operationsverstärker als Impedanzwandler eingesetzt werden (Spannungsfolger). Als weiterer systematischer Messfehler kommen noch die Toleranzen der Widerstände R1…R3 hinzu. Bei 1-%-Metallschichtwiderständen beträgt dieser etwa 2 %. Wenn es genauer sein soll, muss man 0,1-%-Widerstände verwenden oder eine Kalibrierung durchführen. Eine dritte systematische Fehlerquelle ist die Spannung [math]\displaystyle{ V_\text{CC} }[/math], welche normalerweise die Versorgungsspannung bzw. Referenzspannung des ADC ist. Der Einfluss von [math]\displaystyle{ V_\text{CC} }[/math] wird durch den Spannungsteiler etwas abgeschwächt und liegt bei ca. 0,1 bis 1. D. h. 10 mV Fehler von [math]\displaystyle{ V_\text{CC} }[/math] erscheinen als 1…10 mV Fehler auf dem Messsignal. Selbstverständlich muss [math]\displaystyle{ V_\text{CC} }[/math] auch ausreichend stabil und belastbar sein. Der einfache Aufbau wird jedoch mit einigen Nachteilen erkauft.

• relativ geringer Eingangswiderstand
• hoher Ausgangswiderstand
• bei hochohmigen Widerständen sinkt die obere Grenzfrequenz, nur langsame Signale sind dann noch messbar

Als grobe Abschätzung gilt

• [math]\displaystyle{ R_\text{aus}=R_1||R_2||R_3 = \frac{1}{\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}} }[/math]
• [math]\displaystyle{ f_\text{3 dB}=\frac{1}{2 \pi \cdot R_\text{aus} \cdot C_\text{ein}} }[/math]
• Einschränkungen bezüglich der Werte für [math]\displaystyle{ U_\text{ein,min} }[/math], [math]\displaystyle{ U_\text{ein,max} }[/math], [math]\displaystyle{ U_\text{aus,min} }[/math], [math]\displaystyle{ U_\text{aus,max} }[/math]
  • [math]\displaystyle{ U_\text{aus,min} \gt = U_\text{ein,min} }[/math]
  • [math]\displaystyle{ U_\text{aus,max} \gt = U_\text{ein,max} }[/math]
  • [math]\displaystyle{ V_\text{CC} \gt = U_\text{ein,max} }[/math]

([math]\displaystyle{ f_\text{3 dB} }[/math] ist die Frequenz, bei der das Ausgangssignal um 3 dB (≈ 30 % der Spannung) abgefallen ist.)

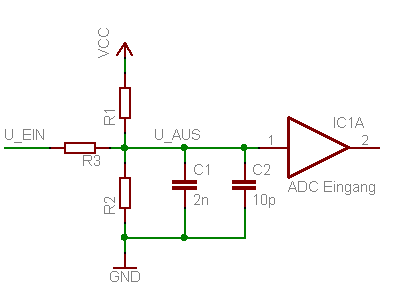
Nachfolgend ist eine praktische Schaltung des Spannungsteilers mit einem AVR-Mikrocontroller gezeigt. Prinzipiell gilt sie natürlich für jeden Mikrocontroller bzw. ADC. Wichtig ist hier der Kondensator C1. Dieser ist notwendig, um kurzzeitig Strom zu liefern, wenn der ADC das Eingangssignal abtastet. Leider sinkt damit auch die obere Grenzfrequenz (siehe Formel für [math]\displaystyle{ f_\text{3 dB} }[/math]). Hier muss ein Kompromiss aus Grenzfrequenz, Ausgangswiderstand und Messfehler gefunden werden. Der Kondensator C2 ist kein diskret platziertes Bauteil, er symbolisiert vielmehr die unvermeidliche Eingangskapazität des ADC.

Spannungsteiler mit Offset, aktiv

Mit etwas mehr Aufwand kann man die genannten Probleme beseitigen. Ein Operationsverstärker bietet hier viele Vorteile.

• sehr hoher Eingangswiderstand
• niedriger Ausgangswiderstand, wichtig zum Speisen von ADC-Eingängen
• [math]\displaystyle{ U_\text{ein,min} }[/math], [math]\displaystyle{ U_\text{ein,max} }[/math], [math]\displaystyle{ U_\text{aus,min} }[/math], [math]\displaystyle{ U_\text{aus,max} }[/math] hängen praktisch nur von der Beschaltung des Operationsverstärker ab.

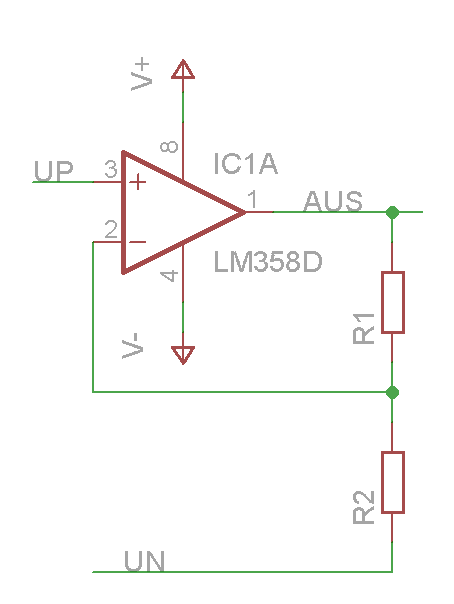
Der mathematische Zusammenhang ist dabei gegeben durch

[math]\displaystyle{ U_\text{AUS} = U_\text{P} \cdot \left( 1 + \frac{R_1}{R_2} \right) - U_\text{N} \cdot \frac{R_1}{R_2} }[/math]

Man kann sowohl UP als auch UN als Eingang benutzen und erhält damit einen invertierenden oder nichtinvertierenden Verstärker mit Offset. Die Berechung der Parameter findet man auch in der Exceltabelle. Wenn die Rechnung negative Zahlen ergibt, ist die gewählte Kombination aus Ein- und Ausgangsspannungsbereich nicht möglich!

Spannungsteiler, der Geheimtip

Oft verwendet man Spannungsteiler, um ein Signal für eine anschließende ADC-Wandlung anzupassen. Verwendet man 15 kΩ und 1 kΩ bzw. 150 kΩ und 10 kΩ, stellt sich ein Teilungsverhältnis von 1:16 ein … welches sehr einfach durch 4fach-Shift im Controller kompensiert werden kann. Das geht wesentlich schneller als die entsprechende Multiplikation.

Messung hochohmiger Widerstände

Will man sehr hochohmige Widerstände messen, die deutlich hochohmiger als der Meßbereich der meisten Multimeter sind (10-50MOhm), so kann man das relativ leicht mittels Spannungsteiler aus Meßobjekt RX und Meßgerät tun. Die allermeisten Digitalmultimeter haben 10 MOhm Eingangswiderstand. Damit läßt sich der gesuchte Widerstand einfach ermitteln. Selbst wenn das Meßobjekt 100 mal hochohmiger als das Multimeter ist (z.B. 1 GOhm), so hat man mit 10V Testspannung immer noch 100mV als Meßwert, welcher relativ sicher und genau gemessen werden kann.

Praktischer Aufbau

• Messung der Spannungsquelle, UT
• Messung in Reihe mit Meßobjekt, U2

[math]\displaystyle{ R_X=(\frac{U_T}{U_2}-1) \cdot 10M\Omega }[/math]

Fehlerrechnung

Bei vielen Meßtechnikanwendungen dient der Spannungsteiler der Einstellung bestimmter Verstärkungsverhaltnisse, um z.B. einen ADC sinnvoll auszusteuern oder auch eine analoge Anzeige zu skalieren. Dabei ist es wichtig, eine Fehlerrechnung durchzuführen, welche eine Aussage macht, inwieweit die Streuung der Bauteile Einfluss nimmt. Dies ist besonders dann wichtig, wenn die Belastung eines Spannungsteilers nicht genau bekannt ist, weil z.B. der Rin eines Chips nur auf 10% bekannt ist. Die klassische Behandlung solcher Unsicherheiten besteht darin, den vorgeschalteten Spannungsteiler entsprechend niederohmig auszulegen. Fließt dort z.B. der 10-fache Strom gegenüber dem belastenden Eingang, so sinkt der Einfluss dessen Ungenauigkeit auf 1:10 - mit dem Resultat, dass er zusammen mit dem vorgeschalteten Spannungsteiler aus 1%-Widerständen zu einem Gesamtfehler von ca 3% führt.

Siehe auch

• Forumsbeitrag: Frequenzkompensierter 10:1-Teiler mit 1 MΩ Impedanz

Weblinks

• Wikipedia-Artikel zum Spannungsteiler
• Youtube-Video: Dynamischer Spannungsteiler für 5kV