Statemachine
Einleitung
Bei einem sogenannten Endlichen Zustandsautomaten (engl. finite state machine, kurz FSM) handelt es sich um die Realisation eines Steuerungskonzeptes, welches eine abstrahierte Maschine zum Vorbild hat, die eine Reihe von Zuständen besitzt, durch die sich ihre Funktion definiert. Diese Maschine arbeitet, indem sie von einem Zustand in einen anderen übergeht und bei den Zustandsübergängen oder dem Verharren in Zuständen bestimmte Aktionen ausführt. Dabei ergibt sich der Folgezustand aus der Kombination des momentanen Zustands und einem externen Ereignis, z. B. einem Tastendruck oder einem Signal aus anderen Bereichen der Software. Dabei wird die Maschine oftmals in verschiedenen Zuständen nur für ganz bestimmte Ereignisse sensibel gemacht.
Die FSM selbst wird immer in irgendeiner Weise über einen Takt angetrieben, kann also nicht in beliebig kurzen Zeitspannen auf Ereignisse reagieren und Zustände wechseln. Der aktive Takt definiert dabei, ob gerade ein Zustandswechsel stattfindet, oder ob in Zuständen verharrt wird. Mit jedem Takt wird anhand des vorliegenden Zustands und dem Status der Eingabekanäle entschieden, welcher Zustand als nächstes vorliegen soll und welche Aktionen dabei auszuführen sind.
Abstrahierte Formen dieser Maschine werden in vielen elektronischen Geräten eingesetzt, um Bedieneraktivitäten und andere Ereignisse im System zu verarbeiten sowie autark ablaufende Prozesse geeignet zu beeinflussen. Entsprechend formulierte FSMs können sowohl in Software auf Prozessoren als auch als eletronische Hardware aufgebaut werden.
Die Beschreibung einer FSM ist auf mehrere Arten möglich. Zum einen kann sie in Form einer Tabelle beschrieben werden, aber auch eine graphische Darstellung der Zustände und deren Abhängigkeiten in Form eines Zustandsdiagramms ist möglich.
Darstellung von Zustandsautomaten
Zustandsautomaten haben den großen Charme, dass es meistens leicht möglich ist, ihre Funktion durch eine Grafik zu veranschaulichen.
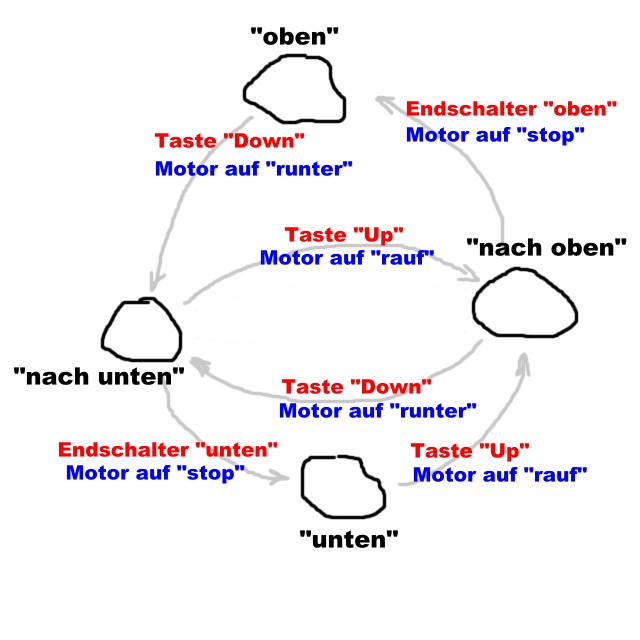
Beispiel: Es ist eine FSM zu entwerfen, die eine Rollosteuerung übernimmt. Es gibt einen Motor, der sich in 3 Zuständen befinden kann: stop, rauf drehend, runter drehend. Außerdem gibt es Endschalter, welche betätigt werden, wenn das Rollo die jeweilige Endposition erreicht hat. Und es gibt 2 Taster "Up" und "Down" durch welche der Benutzer den Bewegungswunsch an die FSM weitergibt. Irgendwie weiß jeder, wie so eine Rollosteuerung funktioniert, und so recht und schlecht kann das auch jeder in der einen oder anderen Form beschreiben. Aber kann man das ganze auch so 'beschreiben', dass man im Vorfeld, vor der Programmierung tatsächlich alle Eventualitäten erfasst und so darstellt, dass auch ein Nicht-Informatiker die Funktionsweise versteht? Genau an dieser Stelle kommt die graphische Darstellung ins Spiel.
Wie sieht nun eine derartige FSM aus? Jede Wolke im Bild sei ein Zustand, dem man einen Namen gibt. Die Pfeile zwischen den Wolken zeigen die Zustandsübergänge an, wobei am Pfeil vermerkt ist, unter welcher Bedingung dieser Übergang genommen werden kann (in Rot) und welche Aktionen dabei auszuführen sind (in Blau).
Aus der Zeichnung ist ablesbar: Befindet sich die Maschine im Zustand "unten" und wird die Taste "Up" gedrückt, dann folgt als Aktion, daß der Motor auf "rauf drehend" gestellt wird und gleichzeitig wechselt die Maschine in den Zustand "nach oben". In diesem Zustand verbleibt die Maschine, während der Motor immer weiter dreht, bis der Endschalter meldet, dass das Rollo oben angekommen ist. Dies ist eine Möglichkeit wie die Maschine den Zustand "nach oben" verlassen kann. In diesem Fall wird dann der Motor abgeschaltet und die Maschine wechselt in den Zustand "oben".
Man sieht hier schon, dass es mit so einer Grafik relativ einfach ist, sich von der korrekten Logik zu überzeugen. In einfachsten Fall legt man zur Simulation einfach einen Gegenstand in die betreffende Wolke, die den gerade aktiven Zustand symbolisiert. Danach geht man alle Möglichkeiten durch, wie diese Maschine von aussen (Taster, Schalter, etc) beeinflusst werden kann und sieht sich an, ob es dafür in der Grafik einen Pfeil gibt, der von der aktiven Wolke wegführt. Gibt es keinen, dann passiert auch nichts. Gibt es einen, dann verschiebt man den Gegenstand in die betreffende Wolke und führt (in Gedanken) die Aktion aus. Auf die Art kann man ganz leicht einige typische Benutzerszenarien durchspielen aber auch ausprobieren, ob man alle Eventualitäten berücksichtigt hat. Denn gerade diese Evantualitäten, an die man am Anfang gar nicht denkt, die sind es, die einem in weiterer Folge oft Probleme bereiten.
Um bei der Rollosteuerung zu bleiben: Was soll denn passieren, wenn das Rollo gerade hochfährt und der Benutzer ein weiteres mal auf "Up" drückt? Oder wenn er auf "Down" drückt? In der Grafik ist ersichtlich, wie in diesem Fall zu verfahren ist. (Und Hand aufs Herz: Hätten Sie daran gedacht, dass diese Fälle zu berücksichtigen sind, als sie 'Rollosteuerung' gelesen haben?)
Implementierungsvariationen
Der konkrete softwaremässige Aufbau einer FSM kann in weiten Grenzen variieren. Das grundlegende Konzept, Aktionen an Zustände zu knüpfen und logische Abläufe an die Abfolge von Zuständen zu binden, bleibt dabei in allen Fällen erhalten. Aber je nach Lust und Laune und dem Können des Programmierers gibt es viele unterschiedliche Möglichkeiten eine FSM zu implementieren. Ziel ist es dabei immer, die eigentliche Maschine, also das was in der Zustandstabelle ausgedrückt wird, so einfach und überschaubar wie möglich zu präsentieren. Sie implementiert die Logik und definiert was die Maschine eigentlich macht und warum sie es macht. Ein einfacher Ansatz ist die Verwendung des C-Konstrukts switch, in der in jedem case-zweig die einzelnen Zustände kodiert werden. Es ist aber auch durchaus möglich eine universelle FSM zu bauen, bei denen eine generische Funktion die Tabelle in Arrayform bekommt und zusammen mit einigen globalen Variablen die Maschine implementiert. Oft wird auch eine Statemaschine dadurch gebaut, indem das zentrale switch-case Konstukt der Sprache [C] durch einen einzelnen Funktionszeiger ersetzt wird und jeder Zustand nichts anderes als eine Funktion ist. Der Übergang von einem Zustand in einen anderen Zustand ist dann nichts anderes als das Zuweisen einer Funktion an diesen Funktionszeiger. Oder aber man kombiniert Tabelle und Funktionszeiger in ein gemeinsames Konzept.
Grundlegender Aufbau
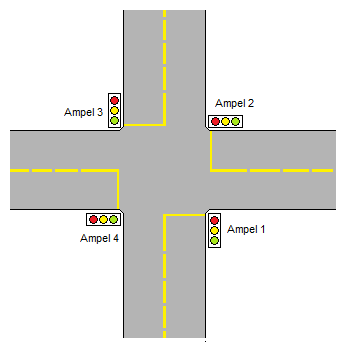
Im Folgenden wird eine FSM in Software verwirklicht, welche die Ampelsteuerung einer Kreuzung übernimmt.
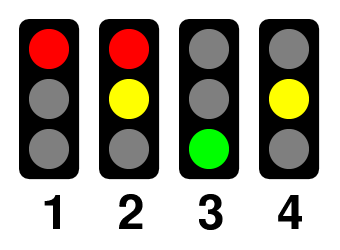
Die Abfolge der Lichtzeichen einer einzelnen Ampel ist dabei
Die komplette Lichtfolge aller Ampeln in der Kreuzung stellt sich dann wie folgt dar: Es ist dabei ausreichend, nur Ampel 1 und Ampel 2 zu betrachten, da Ampel 3 bzw. Ampel 4 die jeweils gleichen Lichtsignale anzeigen. Dies muss nicht immer so sein! Auf einer Kreuzung kann es durchaus für eine Fahrtrichtung Zusatzampeln geben, die die Lichtfolge der Hauptampel modifizieren.
| Zustand | Ampel 1 | Ampel 2 | nächster Zustand |
|---|---|---|---|
| 1 | rot | grün | 2 |
| 2 | rot | gelb | 3 |
| 3 | rot | rot | 4 |
| 4 | rot/gelb | rot | 5 |
| 5 | grün | rot | 6 |
| 6 | gelb | rot | 7 |
| 7 | rot | rot | 8 |
| 8 | rot | rot/gelb | 1 |
Die Zustandsnummer ist in diesem Fall einfach die Taktung der FSM. Verfolgt man die Zustände von einem Zustand zum nächsten, dann kann man sich sehr leicht davon überzeugen, daß die Lichtfolge der beiden Ampeln tatsächlich der gewünschten Abfolge entspricht.
Hat man die Funktionalität einer FSM erst mal soweit in Tabellenform festgelegt, dann ist es sehr einfach daraus ein Programm in einer Programmiersprache wie z.B. C abzuleiten, welches diese Statemachine implementiert.
Kochrezeptartig kann man dabei folgenden Aufbau vornehmen:
- Es gibt eine globale Variable, die den aktuellen Zustand der Maschine repräsentiert. Die Zustände wurden in obiger Tabelle bereits durchnummeriert, so dass es sich anbietet, Zustände innerhalb der Maschine durch ebendiese Zahlen darzustellen.
- Die FSM wird als Funktion implementiert, die für jeden einzelnen Takt aufgerufen wird.
- Jeder Zustand wird innerhalb der Funktion durch einen case innerhalb einer switch Anweisung dargestellt.
- Jeder Zustand kann vor verlassen der Funktion den aktuellen Zustand der FSM beim nächsten Aufruf der Funktion festlegen, indem er an die globale Variable die Nummer des nächsten Zustands zuweist.
- Jegliche Form von Warteschleifen innerhalb der FSM sind verboten. Wenn die FSM auf ein Ereignis warten müsste, dann ist dafür ein eigener Zustand vorzusehen, der auf das Eintreten des Ereignisses prüft und nur dann den nächsten Zustand auswählt, wenn das Ereignis tatsächlich eingetreten ist. Damit erreicht man Multitasking.
- Es ist sinnvoll, den Ampelfarben Namen in Form eines #define oder enums zu geben, damit wird das Konstrukt deutlich leichter lesbar.
#define ROT 1
#define ROT_GELB 2
#define GRUEN 3
#define GELB 4
void Ampel1( unsigned char Farbe ); // schaltet Ampel1 auf eine Farbe
void Ampel2( unsigned char Farbe ); // schaltet Ampel2 auf eine Farbe
unsigned char state = 1; // globale Variable, die den Status repräsentiert
void stateMachine()
{
switch( state ) {
case 1:
Ampel1( ROT );
Ampel2( GRUEN );
state = 2;
break;
case 2:
Ampel1( ROT );
Ampel2( GELB );
state = 3;
break;
case 3:
Ampel1( ROT );
Ampel2( ROT );
state = 4;
break;
case 4:
Ampel1( ROT_GELB );
Ampel2( ROT );
state = 5;
break;
case 5:
Ampel1( GRUEN );
Ampel2( ROT );
state = 6;
break;
case 6:
Ampel1( GELB );
Ampel2( ROT );
state = 7;
break;
case 7:
Ampel1( ROT );
Ampel2( ROT );
state = 8;
break;
case 8:
Ampel1( ROT );
Ampel2( ROT_GELB );
state = 1;
break;
}
}
int main()
{
....
while( 1 ) {
stateMachine();
delay_ms( 1000 );
}
}
Wird diese Funktion im Sekundentakt aufgerufen, so werden die Funktionen Ampel1() bzw. Ampel2() mit der jeweils richtigen Lichtstellung in der richtigen Reihenfolge aufgerufen um die Lichtwechsel der Ampeln einer Kreuzung zu realisieren. Der Einfachheit halber wird in diesem Beispiel die Funktion delay_ms() verwendet. Praktisch wird man in den meisten Fällen besser einen Timer benutzen, um die Statemachine periodisch aufzurufen. Wie das geht und was das für Vorteile hat ist im Artikel Multitasking beschrieben.
Reaktionen auf äußere Ereignisse
Obige Statemaschine ist noch sehr primitiv. Angenommen an dieser Ampelkreuzung gibt es eine Induktionsschleife. Diese sei derartig geschaltet, dass die Hauptrichtung über Ampel2/Ampel4 ständig Grün zeigt und nur bei Annäherung eines Fahrzeugs auf der Strecke Ampel1/Ampel3 wird ein Lichtwechselzyklus durchgeführt, um diesem Fahrzeug die geordnete Durchfahrt zu ermöglichen. Die Statemaschine muss daher auf ein äußeres Ereignis reagieren können. Der Übergang von Zustand 1 in Zustand 2 ist von diesem Ereignis abhängig. Nur wenn es auftritt wird dieser Übergang durchgeführt, ansonsten verbleibt die Maschine im Zustand 1. Die Beschreibung der FSM wird also um einen weiteren Tabelleneintrag ergänzt, in dem festgehalten wird, wie mit dem zusätzlichen Eingang verfahren werden soll. In dieserm erweiterten Beispiel sollen die Zustände mit einem aussagekräftigen Namen versehen werden, denn Menschen sind sehr schlecht im Umgang mit abstrakten Zahlen, sie sind viel besser mit Wörtern vertraut. Die x in der Tabellenspalte "Induktionsschleife" besagen, daß dieses Eingangsignal für die Entscheidungen der Statemaschine keine Rolle spielt (engl. don't care).
| Zustand | Name | Ampel 1 | Ampel 2 | Induktionsschleife | nächster Zustand |
|---|---|---|---|---|---|
| 1 | OSTWEST_GRUEN | rot | grün | ==1 ? | 2 |
| 2 | OSTWEST_GELB | rot | gelb | x | 3 |
| 3 | ALLE_ROT_1 | rot | rot | x | 4 |
| 4 | NORDSUED_ROTGELB | rot/gelb | rot | x | 5 |
| 5 | NORDSUED_GRUEN | grün | rot | x | 6 |
| 6 | NORDSUED_GELB | gelb | rot | x | 7 |
| 7 | ALLE_ROT_2 | rot | rot | x | 8 |
| 8 | OSTWEST_ROTGELB | rot | rot/gelb | x | 1 |
#define ROT 1
#define ROT_GELB 2
#define GRUEN 3
#define GELB 4
void Ampel1( unsigned char Farbe ); // schaltet Ampel1 auf eine Farbe
void Ampel2( unsigned char Farbe ); // schaltet Ampel2 auf eine Farbe
unsigned char Induktionsschleife(); // fragt die Induktionsschleife ab
typedef enum { NORDSUED_ROTGELB, NORDSUED_GRUEN, NORDSUED_GELB, ALLE_ROT_1,
OSTWEST_ROTGELB, OSTWEST_GRUEN, OSTWEST_GELB, ALLE_ROT_2} state_t ;
state_t state = ALLE_ROT_1;
void stateMachine()
{
switch( state ) {
case OSTWEST_GRUEN:
Ampel1( ROT );
Ampel2( GRUEN );
if( Induktionsschleife() ) {
state = OSTWEST_GELB;
}
break;
case OSTWEST_GELB:
Ampel1( ROT );
Ampel2( GELB );
state = ALLE_ROT_1;
break;
case ALLE_ROT_1:
Ampel1( ROT );
Ampel2( ROT );
state = NORDSUED_ROTGELB;
break;
case NORDSUED_ROTGELB:
Ampel1( ROT_GELB );
Ampel2( ROT );
state = NORDSUED_GRUEN;
break;
case NORDSUED_GRUEN:
Ampel1( GRUEN );
Ampel2( ROT );
state = NORDSUED_GELB;
break;
case NORDSUED_GELB:
Ampel1( GELB );
Ampel2( ROT );
state = ALLES_ROT_2;
break;
case ALLES_ROT_2:
Ampel1( ROT );
Ampel2( ROT );
state = OSTWEST_ROTGELB;
break;
case OSTWEST_ROTGELB:
Ampel1( ROT );
Ampel2( ROT_GELB );
state = OSTWEST_GRUEN;
break;
}
}
Warteschleifen
Das Warten auf ein äußeres Ereignis kann mit dem Verzweigen oder auch nicht Verzweigen in einen anderen Zustand realisiert werden. In obiger Statemaschine soll z.B. die Grünphase der Ampel1 von einem Takt auf 5 Takte angehoben werden. Grundfalsch wäre es, dies jetzt mit einer while-Schleife im Zustand 5 zu realisieren. Warten wird immer über zusätzliche Zustände realisiert. Eine Statemaschine darf innerhalb eines Zustands niemals auf etwas warten, sondern muss so schnell als möglich die Kontrolle wieder abgeben. Geht man naiv an die Sache ran, dann könnte man die 5 Takte über die Einführung von zusätzlichen Zuständen leicht erreichen.
| Zustand | Ampel 1 | Ampel 2 | Induktions- schleife |
nächster Zustand |
|---|---|---|---|---|
| 1 | rot | grün | ==1? | 2 |
| 2 | rot | gelb | x | 3 |
| 3 | rot | rot | x | 4 |
| 4 | rot/gelb | rot | x | 5 |
| 5 | grün | rot | x | 9 |
| 6 | gelb | rot | x | 7 |
| 7 | rot | rot | x | 8 |
| 8 | rot | rot/gelb | x | 1 |
| 9 | grün | rot | x | 10 |
| 10 | grün | rot | x | 11 |
| 11 | grün | rot | x | 12 |
| 12 | grün | rot | x | 6 |
Daß ein derartiges Vorgehen bei längeren Wartezeiten oder gar bei berechneter Wartezeitdauer nicht praktikabel ist, dürfte auf der Hand liegen. Besser ist daher die Einführung eines internen Zählers sowie nur eines einzigen, neuen Wartezustands. Beginnt die Wartezeit wird der Zähler auf einen Wert entsprechend der Wartezeit gestellt. Im neuen Zustand wird der Zähler um 1 verringert und nur dann, wenn der Zähler 0 erreicht hat, wird in den ursprünglichen Folgezustand gewechselt. Der Zähler kann also in ähnlicher Form wie die Induktionsschleife als Ereignislieferant aufgefasst werden.
| Zustand | Ampel 1 | Ampel 2 | Induktions- schleife |
Wartezeit | nächster Zustand |
|---|---|---|---|---|---|
| 1 | rot | grün | ==1 ? | x | 2 |
| 2 | rot | gelb | x | x | 3 |
| 3 | rot | rot | x | x | 4 |
| 4 | rot/gelb | rot | x | x | 5 |
| 5 | grün | rot | x | =4 | 9 |
| 6 | gelb | rot | x | x | 7 |
| 7 | rot | rot | x | x | 8 |
| 8 | rot | rot/gelb | x | x | 1 |
| 9 | x | x | x | dec / ==0 ? | 6 |
#define ROT 1
#define ROT_GELB 2
#define GRUEN 3
#define GELB 4
void Ampel1( unsigned char Farbe ); // schaltet Ampel1 auf eine Farbe
void Ampel2( unsigned char Farbe ); // schaltet Ampel2 auf eine Farbe
unsigned char Induktionsschleife(); // fragt die Induktionsschleife ab
typedef enum { NORDSUED_ROTGELB, NORDSUED_GRUEN, NORDSUED_GELB,
ALLE_ROT_1,
OSTWEST_ROTGELB, OSTWEST_GRUEN, OSTWEST_GELB,
ALLE_ROT_2, WARTE_NORDSUED} state_t;
state_t state = ALLE_ROT_1;
unsigned char zaehler;
void stateMachine()
{
switch( state ) {
case OSTWEST_GRUEN:
Ampel1( ROT );
Ampel2( GRUEN );
if( Induktionsschleife() ) {
state = OSTWEST_GELB;
}
break;
case OSTWEST_GELB:
Ampel1( ROT );
Ampel2( GELB );
state = ALLES_ROT_1;
break;
case ALLES_ROT_1:
Ampel1( ROT );
Ampel2( ROT );
state = NORDSUED_ROTGELB;
break;
case NORDSUED_ROTGELB:
Ampel1( ROT_GELB );
Ampel2( ROT );
state = NORDSUED_GRUEN;
break;
case NORDSUED_GRUEN:
Ampel1( GRUEN );
Ampel2( ROT );
zaehler = 4;
state = WARTE_NORDSUED;
break;
case NORDSUED_GELB:
Ampel1( GELB );
Ampel2( ROT );
state = ALLES_ROT_2;
break;
case ALLES_ROT_2:
Ampel1( ROT );
Ampel2( ROT );
state = OSTWEST_ROTGELB;
break;
case OSTWEST_ROTGELB:
Ampel1( ROT );
Ampel2( ROT_GELB );
state = OSTWEST_GRUEN;
break;
case WARTE_NORDSUED:
zaehler = zaehler - 1;
if( zaehler == 0 )
state = NORDSUED_GELB;
break;
}
}
Umsetzung in Tabellenform
Im letzten Beispiel wollen wir die Ampelsteuerung noch etwas realistischer gestalten. Denn die einzelnen Phasen sind unterschiedlich lang, der Zustand Gelb ist deutlich kürzer als der Zustand Grün. Wenn wir also in fast jedem Zustand eine bestimmte Anzahl Takte warten wollen, erscheint es nicht sinnvoll, dafür jedesmal einen neuen Zustand anzuspringen. Sinnvoller ist die Integration des Wartens direkt in den Zustand, so wie im vorherigen Beispiel der Zustand "WARTE_NORDSUED". Dabei fallen jedoch zwei Sachen auf.
- In jedem Zustand muss die Wartezeit des nächsten Zustands zugewiesen werden. Das ist etwas verwirrend.
- Fast alle Anweisungen sind gleich in den Zuständen, nur die Zahlen und der Wert für den nächsten Zustand ändern sich.
Darum soll hier die FSM von einer großen switch Anweisung auf eine Tabelle geändert werden. Das hat den Vorteil, dass die Zustandstabelle nahezu 1:1 in den Quelltext geschrieben werden kann und sie so sehr kompakt und übersichtlich ist. Die eigentliche FSM wird sehr klein und arbeitet sich durch die Tabelle durch. Zur weiteren Verbesserung der Lesbarkeit (siehe Strukturierte Programmierung auf Mikrocontrollern) nutzen wir einen Struct, welche den Zustand der State machine mit sinnvollen Variablennamen beschreibt. Bei dieser Methode muss man beachten, dass die Reihenfolge der Zustände in der enum Definition gleich sein muss mit der Reihenfolge der Zustände in der Tabelle, sonst funktioniert es nicht.
#define ROT 1
#define GRUEN 2
#define GELB 4
#define ROTGELB 5
void Ampel1( unsigned char Farbe ); // schaltet Ampel1 auf eine Farbe
void Ampel2( unsigned char Farbe ); // schaltet Ampel2 auf eine Farbe
int Induktionsschleife(); // fragt die Induktionsschleife ab
typedef enum { OSTWEST_GRUEN=0, OSTWEST_GELB, ALLE_ROT_1,
NORDSUED_ROTGELB, NORDSUED_GRUEN, NORDSUED_GELB, ALLE_ROT_2,
OSTWEST_ROTGELB } state_t;
typedef struct {
int Ampel1;
int Ampel2;
int I_Schleife;
int Wartezeit;
int Naechster;
} ampel_state_t;
state_t state = ALLE_ROT_1;
int zaehler=1;
// Tabelle fuer state machine
ampel_state_t state_table[8] = {
// AMPEL1 AMPEL2 Induktionsschleife ?
// | | | Wartezeit in s
// | | | |
// | | | | naechster Zustand Name
//----------------------------------------------------------------------
{ROT , GRUEN , 1, 10, OSTWEST_GELB}, // OSTWEST_GRUEN
{ROT , GELB , 0, 1, ALLE_ROT_1}, // OSTWEST_GELB
{ROT , ROT , 0, 3, NORDSUED_ROTGELB}, // ALLE_ROT_1
{ROTGELB , ROT , 0, 1, NORDSUED_GRUEN}, // NORDSUED_ROTGELB
{GRUEN , ROT , 0, 10, NORDSUED_GELB}, // NORDSUED_GRUEN
{GELB , ROT , 0, 1, ALLE_ROT_2}, // NORDSUED_GELB
{ROT , ROT , 0, 3, OSTWEST_ROTGELB}, // ALLE_ROT_2
{ROT , ROTGELB , 0, 1, OSTWEST_GRUEN}}; // OSTWEST_ROTGELB
void stateMachine()
{
Ampel1(state_table[state].Ampel1);
Ampel2(state_table[state].Ampel2);
if (zaehler>0) {
zaehler--;
} else {
if ( ((state_table[state].I_Schleife == 1) && Induktionsschleife() ) ||
(state_table[state].I_Schleife == 0) )
{
state = state_table[state].Naechster;
zaehler = state_table[state].Wartezeit;
}
}
}
Implementierung einer objektorientierten Finite State Machine in C++
- Notation von Endlichen Automaten in UML
- Praktisches Beispiel, anhand dessen die Funktionsweise eines Toasters erklärt wird. Dazu wird die Notation in UML verwendet.
- Implementation des Beispiels in C++ auf einem AVR-Controller
Die gezeigte Möglichkeit bzw. das Beispiel sollte als Denkanstoss verstanden werden und nicht als Referenzimplementation. Es wurden bewusst bestimmte Feinheiten von endlichen Automaten verzichtet, um das Beispiel auf gut verständlichem Niveau zu halten.
- Dokumentation im PDF Format ImplementierungEinerFiniteStateMachine_V1.1.pdf
- LaTeX Source der Dokumentation Dokumentation_Source_V1.1.zip
- Beispielcode für AVR-Studio 4 AVR_Beispiel_Source.zip
- Forumsbeitrag: Eine objektorientierte State Machine in C++
Grafische Modellierung einer Finite State Machine
Das Open Source Werkzeug Yakindu Statechart Tools (http://www.statecharts.org) ermöglicht es Zustandsautomaten grafisch zu modellieren, deren Verhalten zu simulieren und Code für verschiedene Sprachen (C/C++, Java) zu generieren. Die grafischen Modellelemente entsprechen denen der UML2 und werden durch eine einfache und zweckmäßige Expression-Language ergänzt.
Einfaches Ampel Modell
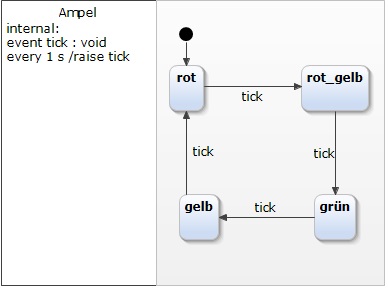
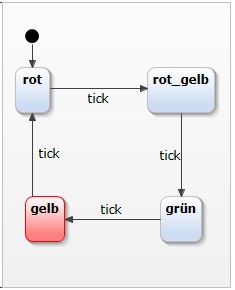
Das Modell einer einfachen Ampel wie oben beschrieben sieht in Yakindu SCT wie folgt aus:
Wie erwartet hat die Ampel vier Zustände, die wiederum mit Übergangs-Pfeilen (Transitionen) verbunden sind. Jede Transition verfügt über einen Auslöser, in diesem Fall mit dem Namen tick Mit Hilfe der Yakindu DSL wird im linken Teil des Editors ein internes Event mit dem Name "tick" definiert, das entsprechend der Taktung des Zustandsautomaten "gefeuert" werden soll. Der Ausdruck every 1s / raise tick sorgt dafür, dass das Event tick jede Sekunde einmal gefeuert wird. Da Yakindu SCT es erlaubt Zustandsautomaten zu simulieren, ist es jederzeit überprüfbar ob das modellierte Verhalten den Erwartungen entspricht. Über Run as... --> YAKINDU Statechart lässt sich in die Simulation View wechseln. Der jeweils aktive Zustand wird nun rot hinterlegt.
Einfache Kreuzung mit Zwei Ampel-Gruppen
Im zweiten Beispiel soll eine einfache Ampelkreuzung modelliert werden. Es wird davon ausgegangen, dass die Ampeln in zwei Gruppen geschaltet werden. Ampel 1 und 3 bilden die nord_süd – Gruppe, während die übrigen Ampeln die ost-west – Gruppe bilden. Der Einfachheit halber werden Ampeln einer Gruppe immer gleich geschaltet. Wie oben darf eine Ampel-Gruppe nur dann den Zustand rot verlassen, wenn die jeweils andere Gruppe sich im Zustand rot befindet.
Im Yakindu SCT Modell gibt es nun für jede Ampel-Gruppe eine eigene Region. Wird der Zustandsautomat betreten so wird nun parallel der Zustand rot in der nord_sued Region und der Zustand gruen in der ost_west Region aktiv. Wie bereits im ersten Beispiel wird der Zustandsautomat über das tick Ereignis angetrieben, das jede Sekunde einmal auftritt. Um das gewünschte Ampel-Verhalten zu modellieren wird nun die Transition von rot zu rot-gelb mit einem Guard, also einer Bedingung geschützt. Zwar wird der Übergang weiterhin mit dem Ereignis tick angestoßen, allerdings wird der Übergang nur ausgeführt wenn die in eckigen Klammern formulierte Boolesche-Bedingung erfüllt ist. Die Funktion active() gehört zu den Bordmitteln von Yakindu SCT und prüft ob ein bestimmter Zustand aktiv ist. In diesem Beispiel kann in der Region nord_sued der Zustand rot nur verlassen werden, wenn in der Region ost-west der Zustand rot aktiv ist. Wie auch im vorhergegangenen Beispiel lässt sich das Verhalten simulieren, so das überprüft werden kann ob das Verhalten den Erwartungen entspricht.
Ampel mit Induktionsschleife
Das Verhalten der Ampelanlage aus Beispiel 2 soll um eine Induktionsschleife erweitert werden. Der Verkehr an der Ampelanlage fließt normalerweise in ost_west – Richtung, daher die Ampel in dieser Richtung immer den Zustand grün haben, es sei denn die Induktionsschleife in nord-süd - Richtung wird ausgelöst.
Um dieses Verhalten in das SCT-Modell zu integrieren muss zunächst ein neues Ereignis definiert werden. Dieses Ereignis wird als Teil des Interface-Scopes definiert, da es außerhalb des Zustandsautomaten erzeugt werden soll. Ereignisse die Teil einer externen Schnittstelle sind werden mit einer Richtung (in / out) deklariert, die angibt ob das Ereignis den Zustandsautomat betritt, oder verlässt.
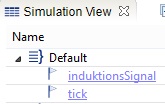
Nach dem das neue Ereignis definiert ist, muss nur noch der Auslöser für den Übergang von gruen zu gelb geändert werden. Statt wie bisher durch das tick Event, wird nun das induktionsSignal als Auslöser verwendet. In der Simulations-Ansicht kann das neue Ereignis manuell mit einem Klick ausgelöst werden, so dass das korrekte Verhalten wieder getestet werden kann.
Warteschleife
Es soll die Grün-Phase verlängert werden, so dass erst nach dem 5. tick der Übergang in den gelb Zustand erfolgt.
Um eine Warteschleife zu realisieren wird dem Internal-Scope zuerst eine neue Variable hinzugefügt. Da während des Wartens der grün Zustand nicht verlassen wird, lässt sich das Herunterzählen der Wartezeit mittels eines zusammengesetzten Zustands darstellen. Wird der Zustand grün betreten, wird zunächst einen Eintritts-Aktion ausgeführt, die den Wert von wartezeit auf 5 setzt. Außerdem wird ebenfalls der Zustand Warten aktiv. Erfolgt nun ein tick wird ohne grün zu verlassen in WartezeitVerringern gewechselt und der Wert von wartezeit um 1 verringert. Der Übergang zu gelb ist wieder durch einen Guard geschützt und kann nur erfolgen wenn die Bedingung wartezeit == 0 erfüllt ist.
C-Code aus dem Modell generieren
Um nun Code aus dem Modell zu generieren muss zuerst eine GeneratorModel-Datei erzeugt werden, in der unter anderem die Ziel-Sprache angegeben wird. Um den Zustandsautomaten abzubilden verwendet die konkrete Implementierung ein switch case Konstrukt, das dem oben Gezeigten ähnelt. Außerdem wurde ein code-only Ansatz verfolgt, so dass keine externen Bibliotheken oder Frameworks benötigt werden. Das komplette Eclipse Projekt kann hier runtergeladen werden.
Realisation von FSMs in Hardware
Aufbau einer FSM in digitalen Chips
Sollen sehr schnelle Steuerungen und Entscheider aufgebaut werden, wurden und werden digitale Bausteine mit Logikgattern verdrahtet, die steuerbare Zähler enthalten. Damit lassen sich effektive Taktgeschwindigkeiten im Bereich von mehreren MHz erreichen, die in Sicherheitsbereichen eingesetzt werden. Oft werden solche Schaltungen auch zur Überwachung von anderen Schaltungsteilen eingesetzt.
Früher wurden fast alle logischen Schaltungen auf diese Weise entworfen, z.B. auch die ersten Computer von IBM.
Umsetzung von FSMs in programmierbarer Hardware
Da heute digitale Hardware vielfach in Form von programmierter PLD- und FPGA-Bausteine realisiert ist, gleicht der Entwurfsprozess der FSMs dem in der klassischen Softwareentwicklung. Dabei besteht je nach Vorliegen der funktionellen Beschreibung und anderer Randbedingungen die Möglichkeit, ein Abbild der digitalen Schaltung in VHDL zu formulieren und zu importieren, bzw. ein klassisches state diagram neu zu entwerfen oder die Zustandswechsel in Tabellenform zu importieren und das Erzeugerwerkzeug die FSM generieren zu lassen, was besonders bei umfangreichen FMSs praktiziert wird.
Letztendlich kann in Hardware jede sequentielle Logikschaltung, welche FlipFlops und Dekoder enthält als FSM betrachtet werden, egal ob es ein einfaches Schieberegister oder eine komplexe ALU einer CPU ist. Die einfachste, denkbare FSM ist ein Toggle-FlipFlop, welches mit jedem Takt seinen Ausgangszustand wechselt.
Geschwindigkeitsvergleich
- In Software realisierte state machines erreichen unter C++ auf Windows-PCs trotz hoher Prozessorleistung selten niedrigere Reaktionszeiten als im Millisekundenbereich. Die damit in Echtzeit erfassbaren und prozessierbaren externen Ereignisse bewegen sich üblicherweise im Bereich von einigen 100Hz. Ein Extrembeispiel ist der USB-3.0-Bus im Zusammenspiel mit HW-IO-Karten: Die Bandbreite lässt ein Laden von Daten mit über 3Gbit im streaming-Modus zu, während im Regelungsbetrieb in der Schleife typische Latenzen von bis zu 10ms auftreten, bis die Reaktion der PC-Software auf eine äußeree Signaländerung auch ausgegeben wurde
- Mit einem Echtzeitbetriebssystem auf einem PC, z. B. Linux mit Preempt-RT Patch, werden ungefähr 35 µs Zykluszeit erreicht, also circa 30 kHz. Trotz des stark verbesserten Treiberssystems unter Linux sind auf PCs auch hier mehrere Millisekunden Latenz zu beobachten.
- Mit Microcontrollern und DSPs erreicht man mit Nicht-Multi-tasking-FSMs Abtastraten bis einige 100kHz. Mit Assembler programmierte Signalprozessoren erreichen Abtastraten bis hin zu 20% ihrer Taktfrequenz, wenn sie direkt auf externe Port-Pins zugreifen.
- In VHDL realisierte state machines besitzen je nach FPGA-Familie, Art der Codierung typische Taktfrequenzen von bis zu 400MHz. Je nach Zyklustiefe laufen damit realisierte FSMs auf bis zu 100MHz und anders als bei DSPs und PCs senkt die Hinzunahme weiterer FMSs nicht deren Schleifen-Frequenz.
Siehe auch
- Multitasking
- Forumsbeitrag: Statemachine: Toller Artikel
Weblinks
- statecharts.online Comprehensive and interactive tutorial on statecharts and state machines
- Using State Machines In Your Designs (C) 2003 Hank Wallace
- Qfsm - A graphical tool for designing finite state machines (GPL)
- itemis CREATE Ein Werkzeug zum Modellieren und Simulieren von Statecharts sowie Code-Generatoren für Java, C und C++.
- www.sinelabore.com Ein Werkzeug das aus UML State Machines C-Code speziell für eingebettete Systeme erzeugt.
- SMC The State Machine Compiler
- C/C++ event driven FSM Open source Werkzeug zur Generierung von C++ FSM Code und UML Diagramm mittels Transitionstabelle.
- http://astade.tigris.org/ -> http://wiki.astade.de/dokuwiki/doku.php (https://www.mikrocontroller.net/search?query=astade)
- Multithreading in C und Arduino von Stefan Frings
- Finite State Machines in Forth von J.V. Noble