Digitale Sinusfunktion
Erzeugung optimierter Sinusfunktionen mit Mikroprozessoren und FPGAs für Anwendungen in der digitalen Signalverarbeitung.
von Jürgen Schuhmacher.
(Auszug aus meinem Artikel "optimized sine wave generation in digital systems").
Die hier beschriebenen Methoden eigenen sich insbesondere zur Umsetzung in low cost Systemen, in denen es auf Geschwindigkeit und Platzersparnis ankommt. Sie gelten für VHDL, Verilog, C und Assembler sinngemäß.
Tabellenbasierte Annäherung
Bei u.a. der klassischen DDS wird die aus einem Akkumulator abgeleitete Phase direkt als Adresse eines RAM/ROM genutzt, in der ein Sinus al Tabelle abgelegt wurde. Diese lässt sich mit Excel leicht erzeugen und analysieren. Danach kann sie in ein Daten-Array in VHDL oder direkt als Definitions-file für die FPGA-internen BRAMs angelegt werden.
Phasendefinition
Gerne wird dabei von der Möglichkeit Gebrauch gemacht, die Gesamtperiode als 4 Teilperioden zu interpretieren, nur die erste zu hinterlegen, bzw. zu erzeugen, um die Welle später phasen- und vorzeichenrichtig wieder zusammenzubauen. Dabei gibt es zwei Möglichkeiten, die Sinuswelle abzubilden:
Randwertdefinition
Man bezieht sich bei den Stützstellen des Sinus auf die Randwerte des abgedeckten Bereiches, also 0.0, 1.0, 2.0, 3.0, ... (n/4)-1 und wiederholt ab dem Punkt n/4 den Bogen rückwärts. Daraus ergibt sich z.B. für 32 Punkte die Abbildung: [0,1,2,3,4,5,6,7] und [8,7,6,5,4,3,2,1] sowie die entsprechende Wiederholung dieses Bogens mit dann negativem Vorzeichen für die Werte ab 180°. Man beachte dabei, dass der "Elementarbogen" bei den Punkten 0, 90, 180 und 270 beginnt, aber den jeweils letzten Wert nicht einschließen darf, da er sonst im nächsten Bereich wiederholt würde. Die Phasen dieser Darstellung entspricht damit p = 0, 1/n, 2/n ... (n-1)/n. Wichtig ist das Teilen durch n und nicht etwas n-1, wie man es teilweise sieht.
Die so generierten Stützstellen rahmen also (erst) mit 9 Werten den vollen Bereich von 0°…90° ein, bzw. mit 17 Werten den Bereich von 0…180° = π. Es gibt zwei leicht verschiedene Viertelbögen, die zueinander nicht symmetrisch sind. Man benötigt gegebenenfalls ein Bit mehr für die Umrechnung (siehe 0…7 und 1…8).
Zwischenwertdefinition
Aus rechnerischer Sicht und auch aus darstellungstechnischen Gründen ist es günstiger, mit den ansteuernden Digitalwerten 0 ... n-1 die Mitte eines Winkelintervalls zu definieren. Damit gibt es pro Viertelbogen genau 8 Stellen, die zur nächsten Viertelperiode voll symmetrisch sind. Der Digitalwert 0 repräsentiert also den mittleren Sinuswert in dem Bereich 0...1, der Digitalwert 7 den Wert im Bereich 7...8. Dazu muss bei der Interpretation der Phase 1/n aufaddiert werden. Die Phase entspricht damit p = 0,5 , 1,5/n, 2,5/n ... (n-0,5)/n. Man kann damit für beide Viertelbögen mit einem gleich großen Vektor arbeiten.
Amplitudenberechnung
In Abhängigkeit der Phase muss die zugehörige Amplitude berechnet werden. Je nach der gewünschten digitalen Aussteuerung braucht man mitunter für nur einen einzigen Wert (den Maxwert) ein Bit mehr. Es sollte daher bedacht werden, ob man unbedingt eine Vollaussteuerung "2 hoch n" benötigt.
Maximalwert-orientiert
Gfs. kann es sinnvoll sein, den Wertebereich nicht voll auszuschöpfen - auch, um die Sinuswelle um einen bestimmten Punkt symmetrisch zu halten. Speziell bei Methode 1 (der Randwertorientierung) liegt ein echter Nullpunkt vor und man ist versucht, den negativen MaxWert (z.B. "-128" bei 8 bit) mitzubenutzen. Eine Optimierung der Werte ist auch mit anderen Zielen möglich:
Fehler-orientiert
Seltener genutzt, aber effektiv wirksamer, als die pauschale Nutzung der maximalen Aussteuerung ist die Optmimierung der Werte - gerade kleiner Tabellen - anhand einer Fehlervorschrift für die Abweichungen, um die durch die Rundung entstehenden Fehler zu minimieren. Anhand der Vorgabe des Maximalwertes sucht man diejenige Zahl für die Aussteuerung, welche in Summe die geringste Abweichung ergibt. Dabei muss entschieden werden, ob es auf den absoluten oder relativen Fehler ankommt. Ist das Ziel die Audiosynthese, währen geringe absolute Fehler anzustreben, weil diese eine additiv überlagerte Störschwinung erzeugen. Für einen einfachen Sinus mit signed INT8 und 8 Werten für die Vierteltabelle sind folgende Werte optimal: 13, 37, 60, 81, 99, 113, 122, 127, erzielt durch eine Aussteuerung von nominell +/-127,75 für den Sinus. Diese Werte treffen nach Rundung die realen Werte besser, als die übliche Multiplikation mit 127 und erzeugen nur etwa 5/8 des mittleren quadratischen Fehlers. Noch besser ist die mit einer Aussteuerung von 121,38 erzielte Wertegruppe von 12, 35, 57, 77, 94, 107, 116, 121. Obwohl die Amplitude kleiner ist, ist sowohl der absolute und relative Fehler geringer. Die Summe der Fehlerquadrate liegt bei einem Viertel der Wertegruppe +/-127! Selbst die niedrig skalierte Sinusfunktion im Bereich +/-99,5 - um unter 100 zu bleiben- , liefert mit den Werten 10, 29, 47, 63, 77, 88, 95, 99 fast genau so gute Werte, wie die vorgestellte "121,38-Gruppe".
Resourcen-orientiert
Durch die geschickte Wahl der Verstärkung können in digitalen Systemen Bits zur Darstellung der Werte eingespart werden.
(Optimierte Tabelle folgt)
Vergleich der Methoden
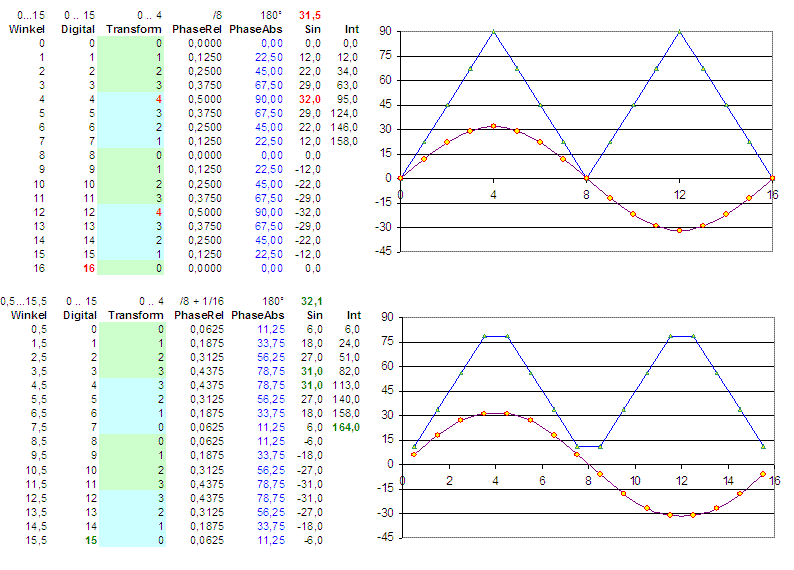
Grafische Veranschaulichung
Erläuterungen zur Grafik:
Dargestellt sind die beiden Methoden beginnend mit jeweils dem Winkel als float-Wert von 0 < X < 16, dem digitalen "code" 0 ... 15, dem abgebildeten Sektor (man beachte den Sonderpunkt 4), der relativen Phase bezogen auf den Definitionsbereich, die absolute Phase innerhalb 360 Grad und der sich Sinuswerte. Die aufaddierten Sinuswerte (int) ergeben einen Eindruck des Integrals = Fläche unter der Kurve. In den Kurven sind die 4 benutzten Punkte dargestellt. Die blaue Kurve gibt den Winkel 0 ... 90 Grad an.
Vorteile der zwischenwertorientierten Methode
Bei Nutzung der Methode 2 ergibt sich der Vorteil, dass sich - gerade bei kleinen Tabellen - eine etwas größere Amplitude unterbringen lässt, da bei gerader Punktanzahl für die Viertelbogen immer Symmetrie zur Zeitachse herrscht. Die Werte liegen also z.B. bei 4 Bit nicht bei 7,6,5 ... -5,-6,-7 unter Verlust des Punktes "-8", der ja möglich wäre, sondern bei 7,5 ... -7.5, womit alle 16 Punkte genutzt werden können und die Welle trotzdem symmetrisch zu 0 bleibt. Ferner fällt der alleinige Maxwert weg, wodurch die Skalierung weiter wachsen kann (z.B. 32,1 im Bild), was besonders bei kleinen Auflösungen relevant ist. Nutzbringend ist der Effekt immer dann, wenn der Wert direkt auf einen Wandler gegeben und geeignet gefiltert wird. So lässt sich in der Tat ein Analogwert von äquivalent 32,000 realisieren, der ausdrücklich nicht ausgegeben werden kann.
Mögliche Probleme
Der Nachteil, dass es bei Methode 2 keinen ausdrücklichen Nullpunkt gibt, ist bei vielen Anwendungen unerheblich - wäre aber im Einzelfall zu prüfen, z.B. wenn ein Motor direkt durch Phase=0 abgeschaltet werden soll und eine echte "0" am Wandlerausgang benötigt wird.
Grundsätzlich muss auch bedacht werden, dass im Falle einer Nachbehandlung der Sinuswellen durch interne digitale Filter generell größere Werte entstehen können, als durch die Stützstellen vorgegeben wurden, was bei größeren Amplituden ein Problem wird. Sicherheitshalber verzichtet man auf die Amplitudenüberhöhung und reduziert diese sogar, z.B. im Hinblick auf Fehlerreduktion, wie oben beschrieben.
Vergleich und Fazit
In der Regel ist Definition 2 vorzuziehen. Bei großen Auflösungen nähern sich beide ohnehin an, es bleibt aber der Vorteil der einfacheren Behandlung der Vektoren und es gibt keine Sonderbehandlung des 90°-Falles. Damit entfallen u.U. Abfragen und das Erzeugersystem arbeitet schneller.[1] Bei Methode 1 bräuchte man je nach Realisierung eine Fallunterscheidung oder ein Bit mehr für die Vollaussteuerung. Gleiches gilt bei der Bildung der Phase.
Eine weitere Betrachtung zu diesem Thema befindet sich hier: http://www.mikrocontroller.net/topic/251921#2593000
Analytische Annäherung
Die Sinuswelle kann durch einen Parabelbogen angenähert werden, wenn eine schnelle Multiplikation zur Verfügung steht:
Sinus-Approximation 1
Die nachfolgende Formel beschreibt dagegen eine einfache Approximation:
- [math]\displaystyle{ \sin(\pi x) \approx 4 x (1-x)\quad \text{wobei}\quad 0 \leqslant x \leqslant 1 }[/math]
Der Faktor 4 ist so gewählt, dass der Scheitel der Parabel mit dem Maximum der sin-Kurve zusammenfällt. Die Abweichung dieses leicht oberhalb des Sinus verlaufenden Bogens beträgt nicht mehr als 12.5%[2] und eignet sich daher für viele Applikationen, bei denen es nicht auf 100% Genauigkeit ankommt, oder die Abweichung akzeptabel ist.
Nutzt man neben der Grundwelle auch jeweils Oberwellen, also Vielfache des Eingangsvektors, können die in der Quadratfunktion gemäß Laplace enthaltenen Oberwellen stückweise eliminiert werden, indem sie passend abgezogen werden. Dazu sind die Koeffizienten der entstehenden neuen Oberwellen iterativ zu berücksichtigen. Allein durch schon durch die amplitudenrichtige gegenphasige Zumischung der dritten Oberwelle kann der Fehler bereits auf unter 1% gesenkt werden. Durch Zumischung der Oberwellen 5 und 7 erreicht man einen Sinus besser als 50dB(sfdr), wobei die 9. Oberwelle automatisch mit wegfällt, da die abzuziehende 3. Oberwelle ihrerseits eine dritte enthält, welche exakt die Amplidude besitzt, welche in der Grundfunktion zuviel enthalten ist.
Sinus-Approximation 2
Durch Anwendung von angepassten Korrekturwerten, die aus Vielfachen der anregenden Frequenz gewonnen werden, können die Oberwellen im Endwert reduziert werden. Der Definitionsbereich wird dabei einfach durch Multiplikation des Einspeisevektors mit einem größeren Faktor abgetastet, wobei ab den Oberwellen 4 und folgende der resultierende Y-Wert zwischen zwei Nulldurchgängen manuell invertiert werden muss, um den jeweils inversen Halbbogen zu bilden. In C kann das durch die Signum/ABS-Funktionen erfolgen, in VHDL durch Nutzung des jeweiligen entstehenden MSBs. Die resultierenden Funktionen für die Oberwellen Y2 ... Y5 werden mit geeigneten Korrekturfaktoren multipliziert und addiert, sodass sich die Fehler minimieren.
Im obigen Beispiel wurde für die Abbildung des benötigten Sinus-Viertels ein 8Bit-Vektor (0...255) angenommen und 4 Oberwellen herangezogen. Die Phase wird daher auf 10Bit => 1/1024 genau abgebildet. Die Koeffizienten lauten:
k1 = 1,0000, k2= -0,0444, k3= -0,0207, k4= -0,0018, k5= -0,00255.
Die Abweichung des Ausgangswertes vom idealen Sinus (grün) beträgt hier ca. +/-45 digit pro Vollaussteuerung (hier 65536), was bewirkt, dass man mit der obenstehenden Vorschrift durch Weglassen der unteren 5 Bits einen Endwert mit +/- 1 digit Fehler (~ 0,1% Genauigkeit) erzielen kann, was gut zur gewählten Phasenauflösung passt.
Eine in VHDL realisierte Schaltung läuft in einem Altera Cyclone FPGA rein kombinatorisch mit nahezu 50MHz.
Weiterverarbeitung
Bei der direkten Erzeugung des Wertes durch Formeln kann die Berechnung mit jeder beliebigen Auflösung erfolgen. Eine Interpolation oder Filterung ist in diesen Fällen nicht unbedingt nötig. Um dennoch Zwischenwerte zu bekommen gibt, es folgende Möglichkeiten:
Interpolation
Die bisher nicht genutzten unteren Bits des Phasenakkumulators werden in eine Geradengleichung eingesetzt, wobei die Steigung und der Achsenabschnitt aus dem aktuellen und dem nächsten Punkt gewonnen werden. Wird eine Tabelle benutzt und neben dem Sinus auch der Cosinus erzeugt, so gibt die jeweils andere Funktion bereits die Steigung an und kann mitverwendet werden. Für schnelle Applikationen lohnt sich in jedem Fall die ausdrückliche Hinterlegung der Steigung.
Durch die Nutzung einer Interpolation werden die Artefakte infolge der begrenzten Tabellengröße stark gemindert. Für erweiterte Ansprüche werden zuweilen wavelets oder quadratische Bögen als Interpolationsfunktion verwendet, oftmals ist aber eine einfache Filterung zweckmäßiger:
Filterung
Eine anschließende Filterung kann die Güte des Sinus weiter erhöhen. Ein einfaches, auf die zu erzeugende Frequenz abgestimmtes, IIR-Filter dämpft zuverlässig die hochfrequenten Anteile, also die verbleibenden "Knicke" der Interpolation. Die einfachste Implementierung ist ein Filter mit binären Koeffizienten vom Typ: Y(t+1) = Y(t) - Y(t)/k + SinusWert/k, wobei k = 16,32,64 ...!
Eine Filterung ist insbesondere dann vorteilhaft, wenn ein Umsteuern der Frequenz erfolgt und Phasensprünge geglättet werden sollen.
Anwendungsbeispiele
Signalsynthese
Tongeneration
In den 80ern konnte ich (in Assembler!) so ohne Interpolation oder Filterung wie bei einer DDS arbeiten und mit dem VC20 und VC64 Pseudo-Sinustöne erzeugen, die in der Frequenz genau zu variieren waren. Bei nur ca. 2MHz Taktfrequenz liessen sich mit einer einfachen Schleife schon bei 64 Punkten Sweeps und kontinuierliche Portamentoeffekte für das komplette Audiospektrum mehrkanalig produzieren. Die im Signal freilich enthaltenen Oberwellen wirken dabei mit zusätzlicher Musikalität :-)
Motorsteuerung
Bei dem Betrieb von Schrittmotoren werden die X/Y-Wicklungen mit Strömen angesteuert, die Sinus/Cosinus-Verläufe aufweisen, um einen Feinschrittbetrieb zu ermöglichen. Die im Signal enthaltenen Oberwellen sind hier sogar günstig für den Beschleunigungsverlauf, da die Steigungen der Funktion genau dort größer sind, als der echte Sinus, wo der Motor aufgrund des Haltemoments am meisten Widerstand entgegen setzt. (Nur ein Motor ohne Haltemomentpunkte würde 100%ige COS/SIN benötigen).
Signalverarbeitung
Fensterung
Durch partielle Nutzung der Halbbögen der Sinusapproximation 1 kann in einfacher Weise eine effektive Fensterfunktion für Filter und FFTs erzeugt werden.
IQ-Modulation
Der Vorteil der kontinuierlichen, nicht an Tabellen gebundenen, Sinussynthese zeigt sich besonders bei der IQ-Modulation, wo die Akkumulatorrundung bei kleinen Tabellen ohne eine Interpolation zu weiterem unerwünschtem Phasenrauschen führt, das mitunter schwerwiegendere Fehler generiert, als der systematische Amplitudenfehler. Allerdings ist zumindest Annäherung 2 zu verwenden.
Verzerrer
Durch parametrische Addition der so erzeugen Quasi-Sinushalbwelle zwischen -100% und +100% zu einem Signal lassen sich einfache Signalkompressoren und Verzerrer konstruieren, die sehr homogen arbeiten.
Diese sind z.B. in der in der Tonstudio / Audiotechnik oder der Industrie im Bereich non-linear-predistortion zur Ansteuerung von frequenzabhängigen Filtern und Korrektur von nichtlinearen Systemen wie Magnetik anwendbar.
Fußnoten
- ↑ Unterschied AVR 8 Bit mit 10MHz und 256 Sinusstellen: 16% weniger Rechenzeitbedarf!
- ↑ Die maximale Abweichung wird für x ≈ 0.15 bzw. x ≈ 0.85 erreicht. Eine kleinere absolute Abweichung kann für eine etwas kleinere Konstante auf der rechten Seite erreicht werden, d.h. für ca. 3,848 anstatt der 4,0.
Links
Diskussion um DDS:
Suche im Forum nach