Operationsverstärker-Grundschaltungen
Idealisiertes Modell eines OPV
Anschlüsse
Ein Operationsverstärker hat zwei Eingänge (+) und (-) und einen Ausgang (UA). Außerdem verfügt er über eine positive und eine negative Spannungsversorgung (V+) und (V-).
Spannungsversorgungen
Die Spannungsversorgungen sollen zunächst nicht interessieren. Sie werden in Schaltungen oft nicht eingezeichnet. In der Praxis ist es jedoch wichtig zu wissen, dass die Ausgangsspannung immer zwischen (V+) und (V-) liegt. Die Ausgangsspannung des OPV kommt schließlich dadurch zustande, dass der Ausgang über einen Transistor mehr oder weniger hochohmig mit den beiden Versorgungsspannungen verbunden wird.
Wenn man einen OPV also mit +5V versorgt, so kann der OPV im besten Fall am Ausgang +5V erzeugen. Man würde in diesem Fall von einem "Rail-to-Rail" Operationsverstärker sprechen. Bei vielen Operationsverstärkern ist die maximal mögliche Ausgangsspannung geringer als die Versorgungsspannung. Ein mit +5V Spannungsversorgung beschalteter OPV kann dann beispielsweise nur +4V Ausgangsspannung erzeugen.
Ausgang
Der Ausgang des OPV ist eine ideale Spannungsquelle. Das bedeutet, dass die Ausgangsspannung unabhängig davon ist, was ausgangsseitig an den OPV angeschlossen wird. In der Praxis gilt dieses Modell häufig nur bei "sinnvollen Anwendungen". So ist beispielsweise der Ausgangsstrom des OPV nach oben begrenzt (typischerweise im mA-Bereich), und manche OPV schwingen sehr leicht, wenn man sie kapazitiv belastet.
Eingänge
Die Eingänge eines OPV sind hochohmig, d. h., es handelt sich nur um "Messfühler", die keinen Strom führen. Achtung: Die Eingangsschutzbeschaltung (Dioden von GND und gegen VCC) bei manchen OPVs kann jedoch dazu führen, dass Strom in den Eingang fliesst, wenn dessen Betriebsspannung z.B. abgeschaltet ist.
Funktionsweise
Der OPV mißt zu jeder Zeit die Differenz [math]\displaystyle{ U_D = U(+) - U(-) }[/math] der Eingangsspannungen.
Ist die Spannung an (+) größer als an (-), so erhöht der OPV die Ausgangsspannung. Ist die Spannung an (+) niedriger als an (-), so vermindert der OPV die Ausgangsspannung.
Das Ergebnis dieses Vorgangs wird häufig über die Gleichung:
[math]\displaystyle{ U_a = v \cdot U_D }[/math]
beschrieben, wobei [math]\displaystyle{ v }[/math] eine sehr große Zahl (10^4...10^6) ist.
Mit Hilfe der beschriebenen Funktionsweise lassen sich alle grundlegenden Schaltungen herleiten.
Beispiel
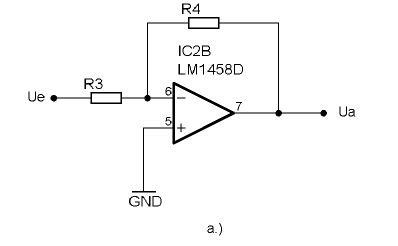
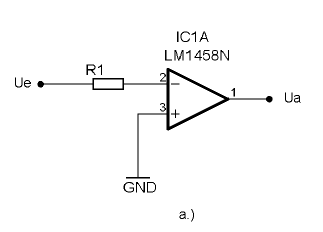
Betrachtet wird die invertierende Grundschaltung nach Abbildung a) im Abschnitt Verstärkergrundschaltungen.
Für die Pfeilrichtungen der Spannungen und Ströme gilt:
- [math]\displaystyle{ U_e }[/math]: von oben nach unten
- [math]\displaystyle{ I_{R3} }[/math]: von links nach rechts
Die Spannung am (+)Eingang ist gleich Null. Die Spannung am (-)Eingang wird durch die Spannungsquelle [math]\displaystyle{ U_e }[/math] und durch die im OPV befindliche und mit dem Ausgang verbundene Spannungsquelle des OPV manipuliert.
- Ist die Spannung am (-)Eingang negativ, so erhöht der Operationsverstärker die Ausgangsspannung. Dadurch wird durch die Rückführung über den Widerstand auch die Spannung am (-)Eingang positiver. Und zwar so lange, bis die Spannung am (-)Eingang gleich groß ist, wie die Spannung am (+)Eingang, also U(-)=0V.
- Ist die Spannung am (-)Eingang positiv, so vermindert der Operationsverstärker die Ausgangsspannung. Dadurch wird durch die Rückführung über den Widerstand auch die Spannung am (-)Eingang negativer. Und zwar so lange, bis die Spannung am (-)Eingang gleich groß ist, wie die Spannung am (+)Eingang, also U(-)=0V.
Der Operationsverstärker wird also die Spannungen an (+) und (-) angleichen. Das passiert immer dann, wenn der Ausgang mit dem (-)Eingang verbunden ist. Der Trick in dieser Schaltung besteht darin, dass von der Ausgangsspannung nur ein Teil wieder rückgeführt wird. Die Spannung U_e ist daher höher, als der Teil der benötigt wird, um die Spannungen an den Eingängen aneinander anzugleichen. Man nennt das Prinzip "Gegenkopplung". Auf diese Art und Weise funktionieren alle analogen OPV-Schaltungen.
Da an (+) Massepotential anliegt, wird somit auch (-) daran angeglichen, und so liegt an [math]\displaystyle{ R_3 }[/math] die Spannung [math]\displaystyle{ U_e }[/math] an. Daher gilt: [math]\displaystyle{ I_{R3}=\frac{U_e}{R_3}. }[/math]
Da der (-)Eingang hochohmig ist, fließt [math]\displaystyle{ I_{R3} }[/math] über [math]\displaystyle{ R_4 }[/math] weiter zum OPV-Ausgang.
Ua ist die Spannung vom Ausgang zur (virtuellen) Masse am (-)Eingang. (--> Pfeil einzeichnen und klarmachen, daß es egal ist, ob der Pfeil vom Ausgang zur Masse geht oder vom Ausgang "entgegen der Stromrichtung" zur virtuellen Masse an (-)!)
Mit Hilfe von [math]\displaystyle{ I_{R3}=\frac{U_e}{R_3} }[/math] ergibt sich:
[math]\displaystyle{ U_a = -R_4 \cdot I_{R3} = -{{R_4} \over {R_3}} \cdot U_e. }[/math]
Die Energie für den Stromtransport über [math]\displaystyle{ R_4 }[/math] stammt vom OPV! Sobald die Ladungen ausgehend von der Spannungsquelle [math]\displaystyle{ U_e }[/math] die virtuelle Masse an (-) erreicht haben, hat [math]\displaystyle{ U_e }[/math] seine gesamte Energie abgegeben.
Reale OPVs / Kennwerte
Abweichend vom idealen OPV besitzen reale OPVs diverse Einschränkungen und Kennwerte, die sie für verschiedene Einsätze mehr oder weniger prädestinieren.
Leerlaufverstärkung
Die Leerlaufverstärkung gibt an, wie stark sich das Ausgangssignal i.A. der Änderung eines Eingangsignals statisch ändert, bzw nach dem Einschwingen erreichen könnte, wenn es nicht durch die Betriebsgrenzen limitiert wäre.
Verstärkungs-Bandbreiteprodukt
Das Verstärkungs-Bandbreiteprodukt gibt an, bei welcher Verstärkung welche Bandbreite erreicht werden kann. Durch Rückkopplung kann die Verstärkung eingestellt werden. Bei kleinerer Verstärkung ergibt sich somit eine höhere Bandbreite, wenn das Produkt aus beiden konstant ist. Die Bandbreite bei der Verstärkung eins heißt Transitfrequenz (englisch "Unity Gain Frequency"). Das Verstärkungs-Bandbreiteprodukt ist entscheidend für das Kleinsignalverhalten.
Anstiegsgeschwindigkeit
Bestimmend für das Großsignalverhalten ist neben dem Verstärkungs-Bandbreiteprodukt die Anstiegsgeschwindigkeit (slew rate), da bei hohen Ausgangsamplituden die Ausgangskurve eventuell zu steil wird, um richtig wiedergegeben zu werden.
Gleichtaktverstärkung
Infolge des inhomogenen Aufbaus der internen Verstärkerstufen werden die beiden Eingangssignale nicht exakt gleich verstärkt, was in einen Gleichanteil und einen Differenzanteil aufgeteilt werden kann. Die nicht erwünschte Gleichtaktverstärkung bzw. ihr Gegenstück, die Gleichtaktunterdrückung (engl. common mode rejection ratio, CMRR) ist dabei ein Maß für die Qualität des OPVs. Klassische (VFB) OPV haben immer ein mit der Frequenz fallendes (-20 dB/Dekade) CMRR.
Ein- und Ausgangsbereich
Wie weiter oben schon angesprochen ist die Ausgangsspannung eines OPVs begrenzt von der Versorgungsspannung und dem internen Aufbau des OPVs. Standard-OPV erreichen meist einen Ausgangsbereich, der bis circa 1-2 V an Versorgungsspannungen heran reicht, während sogenannte Rail-to-Rail (R2R) OPV sehr nah (bei niedriger Last bis auf wenige mV) an die Versorgungsspannungen herankommt. Das ist jedoch mit Abstrichen verbunden, sodass es in der Regel besser ist R2R OPV nur wenn nötig zu verwenden.
Ähnliche Beschränkungen gibt es auch für die Eingänge eines OPVs, hier werden im Wesentlichen drei Arten unterschieden:
- Klassisch: Eingangsspannung darf nur bis wenige Volt an die Versorgung herankommen.
- Ground-Sensing: Die Eingangsspannung darf bis zur negativen Versorgung heruntergehen, klassische Vertreter sind LM324/LM358.
- Rail-to-Rail Input/Output (RRIO): R2R OPV, wo sowohl Eingänge als auch Ausgänge bis an die Versorgungsspannungen reichen.
Bei klassischen Operationsverstärkern ist zu beachten, dass manche ein Verhalten namens phase reversal (Phasenumkehr) zeigen, wenn die Eingangsspannung den zulässigen Bereich überschreitet. Bei der Phasenumkehr dreht sich die Phase in der Eingangsstufe des OPVs um 180° und Rückkopplung wird zur Mitkopplung. Ein bekannter Vertreter dieser Art ist die TL06x/TL07x/TL08x Familie von OPV.
Verstärkergrundschaltungen
Grundbeschaltung mit Berechnung
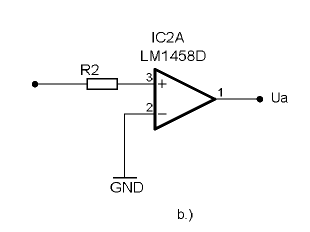
In a) und b) verwenden wir den OPV als Verstärker und nutzen hier die Möglichkeit der Gegenkopplung, um definierte Verstärkungen zu erhalten. Wir gehen wieder davon aus, dass der OPV ein ideales Bauteil ist und daher seine Leerlaufverstärkung unendlich ist. Ebenso betrachten wir den Eingangswiderstand als unendlich.
In a) ist ein invertierender Verstärker mit einem OPV dargestellt. Durch die Widerstände R3 und R4 wird die Verstärkung bestimmt:
- [math]\displaystyle{ V = \frac{U_a}{U_e} = -\frac{R_4}{R_3} }[/math]
Das Verhältnis der beiden Widerstände bestimmt also die Verstärkung und somit die Ausgangsspannung:
- [math]\displaystyle{ U_a = -\frac{R_4}{R_3} \cdot U_e }[/math]
oder auch
- [math]\displaystyle{ U_a = V \cdot U_e }[/math]
Das negative Vorzeichen drückt aus, dass es sich um einen invertierenden Verstärker handelt.
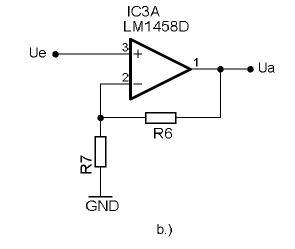
Beim nichtinvertierenden Verstärker b) finden wir auch eine Rückkopplung über R6 zum invertierenden Eingang des OPVs. Die Verstärkung wird durch das Gegenkopplungsnetzwerk R6 und R7 bestimmt. Hier ist:
- [math]\displaystyle{ V = 1 + \frac{R_6}{R_7} }[/math]
Eine Verstärkung von 1 ist sinnvoll, wenn eingangsseitig eine Spannungsquelle mit hohem Innenwiderstand verwendet wird. Für [math]\displaystyle{ \frac{R_6}{R_7} \to 0 }[/math] heißt die Schaltung "Spannungsfolger".
Kleinere Werte als 1 lassen sich nicht realisieren. Die Ausgangsspannung errechnet sich also so:
- [math]\displaystyle{ U_a = U_e \cdot \left (1 + \frac{R_6}{R_7}\right ) }[/math]
Beispiel: Eine Eingangsspannung von 0,5 V soll auf den Wert 5 V verstärkt werden, es ist also eine Verstärkung V von 10 benötigt. R7 ist mit 10 kΩ vorgegeben. Also ist das Verhältnis
- [math]\displaystyle{ \frac{R_6}{R_7} = V - 1 }[/math]
Bei einem Wert von 10 kΩ für R7 errechnet sich R6 zu
- [math]\displaystyle{ R_6 = (V - 1) \cdot R_7 = (10 - 1) \cdot 10\,\mathrm{k\Omega} = 90\,\mathrm{k\Omega} }[/math]
Die Ausgangsspannung Ua wird also:
- [math]\displaystyle{ U_a = U_e \cdot \left (1 + \frac{R_6}{R_7}\right ) = 0{,}5\,\mathrm{V} \cdot \left (1 + \frac{90\,\mathrm{k\Omega}}{10\,\mathrm{k\Omega}}\right) = 5\,\mathrm{V} }[/math]
Nichtinvertierender Verstärker mit Offset
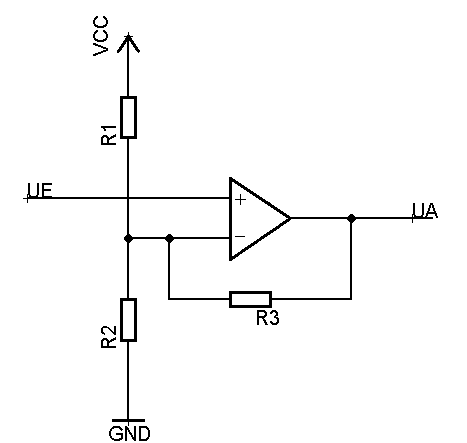
Eine Abwandlung des nichtinvertierenden Verstärkers erlaubt es, einen konstanten Offset vorzugeben. D.h. von der zu verstärkenden Eingangsspannung U(e) wird eine konstante Spannung U(o) abgezogen und die Differenz verstärkt. Auf der Ausgangsspannung U(a) findet sich die Offsetspannung U(o) allerdings wieder.
Es gilt:
Offsetspannung:
- [math]\displaystyle{ U_o = U_V \cdot \frac{R_2}{R_1 + R_2} }[/math]
mit U(V) = Versorgungsspannung an R1
Verstärkung:
- [math]\displaystyle{ V = 1 + \frac{R_3}{\frac{R_1 \cdot R_2}{R_1 + R_2}} }[/math]
Ausgangsspannung:
- [math]\displaystyle{ U_a = (U_e - U_o) \cdot V + U_o }[/math]
Der Vorteil dieser Schaltung ist, daß nur die Differenz verstärkt wird. Damit kann eine größere Verstärkung gewählt werden. Zu berücksichtigen ist dabei, dass die Ausgangsspannung U(a) um die Offsetspannung U(o) verschoben ist.
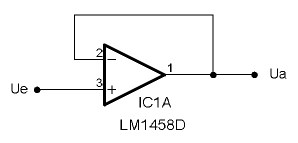
Spannungsfolger (Impedanzwandler)
Eine Abart des nichtinvertierenden Verstärkers stellt der Spannungsfolger dar. Beim nichtinvertierenden Verstärker errechnet sich die Ausgangsspannung aus:
- [math]\displaystyle{ U_a = U_e \cdot \left (1 + \frac{R_2}{R_1}\right ) }[/math]
Wenn wir R2 auf 0Ω (mit R1 > 0) oder R1 auf unendlich (mit R2 < ∞) ändern, erhalten wir daher:
- [math]\displaystyle{ V = 1 + \frac{R_2}{R_1} = 1 }[/math]
Ein Spannungsfolger hat also eine Verstärkung V von 1.
Umgezeichnet sieht die Schaltung dann so aus:
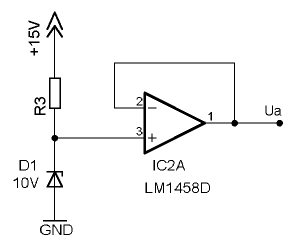
Man erhält den klassischen Elektrometerverstärker. Der Zweck dieser Schaltung ist die sogenannte Impedanzwandlung. Man nutzt die Eigenschaft, dass ein idealer OP einen unendlichen Eingangswiderstand und einen Ausgangswiderstand von 0Ω hat. Zwar sieht das real natürlich anders aus - so liegt der Eingangswiderstand Re bei normalen OPs in der Größenordnung von 1MOhm bis [math]\displaystyle{ 10^{15} \Omega }[/math], der Ausgangswiderstand Ra im Bereich 20Ω bis 1kOhm - trotzdem kann man mit einer solchen Schaltung aus einer relativ hochohmigen Spannungsquelle eine niederohmige, durch Folgeschaltungen belastbare Spannungsquelle machen.
In dem nebenstehenden Beispiel ist eine einfache Möglichkeit zur Erzeugung einer Referenzspannung gezeigt: Es kommt eine normale Stabilisierungsschaltung mit einer Z-Diode (früher "Zenerdiode") und einem Widerstand zur Anwendung, die aber nicht mehr die schlechten Eigenschaften der Standardbeschaltung hat. Trotz des steilen Durchbruchverhaltens einer Z-enerdiode hängt die genaue Spannung davon ab, welcher Strom durch sie fließt. Dieser Strom würde sich aber ändern, wenn ein Verbraucher die Zenerdiode direkt mit einem ungleichmäßigen Stromfluss belasten würde. Als Folge davon würde die Spannungslage der Zenerdiode je nach Verbraucherlast schwanken. Durch den Spannungsfolger wird das verhindert, weil dieser den vom Verbraucher gezogenen Strom bereitstellt und durch den Widerstand an der Z-Diode praktisch immer derselbe Strom fließt. Ein Einfluss ist nur noch durch die Versorgungsspannung gegeben, weil deren Änderung einen minimal geänderten Stromfluss in der Z-Diode auslöst, der bei großen Änderungen wieder Spannungsänderungen bewirkt. Bei Chips in denen sehr genaue Spannungen benötigt werden, kommen daher 2 verkettete Stufen dieser Art zum Einsatz. Die erste stabilisiert den Eingang, die zweite den Ausgang.
Eine weitere Anwendungsmöglichkeit wäre das hochohmige Auskoppeln einer Brückenspannung. Die Brückenschaltung selbst wird durch Folgeschaltungen nicht mehr belastet, alle anderen Eigenschaften bleiben erhalten.
Der Komparator
In der einfachsten Beschaltung des Operationsverstärkers erhält man einen Komparator. Es fällt auf, dass kein Gegenkopplungsnetzwerk vorhanden ist. Der OP arbeitet daher mit seiner vollen Leerlaufverstärkung Vo. Dies bedeutet, dass bereits eine kleine Eingangsspannung genügt, um den OP in die Begrenzung zu treiben. Das heißt, die Ausgangsspannung Ua wird annähernd die Betriebsspannung erreichen.
Achtung: nicht jeder OP ist als Komparator verwendbar! Manche haben Schutzdioden zwischen invertierendem und nichtinvertierendem Eingang, die bei einem zu großen Spannungsunterschied das Signal kurzschließen. Ob das bei einem konkreten OP-Typ der Fall ist, findet man im Datenblatt: bei den absolute maximum ratings ist die "Differential Input Voltage" angegeben. Wenn dort nur 1 bis 2 Volt stehen, ist der OP nicht als Komparator einsetzbar. Die sichere Alternative ist jedoch, einen speziellen Komparator-IC zu verwenden. Diese sind im Grunde auch nur OPs, aber für den Komparator-Betrieb optimiert.
Beim Komparator gibt es zwei Möglichkeiten der Beschaltung: die invertierende nach a) und die nichtinvertierende Beschaltung nach b).
Berechnungsbeispiel für Schaltung b)
Angenommen die Leerlaufverstärkung Vo von 40000 und eine Eingangsspannung von 0,1 Volt. Die Betriebsspannungen Vcc und Vee legen wir auf +/- 24 V fest. Damit ergibt sich theoretisch für Ua:
- [math]\displaystyle{ U_a = V_0 \cdot U_e = 40000 \cdot 0{,}1\,\mathrm{V} = 4000\,\mathrm{V} }[/math]
Das ist natürlich ein unrealistischer Wert, da Ua nicht höher sein kann als die Betriebsspannung. Also anders ausgedrückt: Bei welcher Spannung Ue erreicht der OP seine Aussteuerungsgrenze?
- [math]\displaystyle{ U_e = V_{cc} / V_0 = 24\,\mathrm{V} / 40000 = 0{,}6\,\mathrm{mV} }[/math]
Das bedeutet, dass eine Spannung von 0,6 mV ausreicht um den Komparator in die Begrenzung zu treiben.
Das gleiche gilt auch für den invertierenden Komparator, allerdings wird hier der OP in die negative Begrenzung gebracht.
- [math]\displaystyle{ -U_a = V_0 \cdot U_e }[/math]
Diese beiden einfachsten Komparatorschaltungen werden so nur sehr selten verwendet, weil sie keine Hysterese haben. D.h. es gibt nur eine Umschaltschwelle. Dadurch kann der Ausgang schwingen, wenn das Eingangssignal sehr nah an der Umschaltschwelle liegt, weil kleinste Störungen im Signal den Komparator mehrfach schalten lassen (dafür reichen wenige mV!). Ausserdem sind Operationsverstärker als Komparator relativ langsam, das liegt am inneren Aufbau. Echte Komparatoren sind deutlich schneller und sie haben auch kein Problem damit, wenn der Ausgang in die Sättigung geht. Darum beschaltet man einen OPV bzw. Komparator meistens mit Hysterese. Das nennt man dann einen Schmitt-Trigger.
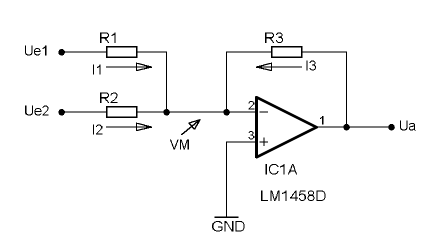
Der Addierer (Summierverstärker)
Ein als invertierender Verstärker beschalteter OP lässt sich so beschalten, dass ein Summensignal aus den Eingangsspannungen gebildet wird. Um die Funktion deutlich zu machen, ist eine Betrachtung der einzelnen Ströme nötig.
In einem invertierenden Verstärker wird sich die Ausgangsspannung immer so einstellen, dass der invertierende Eingang Massepotential hat. Die virtuelle Masse (VM) unterscheidet sich von einer "normalen" Masse dadurch, dass das Potential durch einen Regelungsvorgang zustande kommt. An der virtuellen Masse (VM) gilt die Knotenpunktregel, wonach die Summe der zufließenden Ströme gleich der Summe der abfließenden Ströme ist.
- [math]\displaystyle{ I_1 + I_2 = -I_3 }[/math]
Sofern [math]\displaystyle{ U_{e1} }[/math] und [math]\displaystyle{ U_{e2} }[/math] bekannt sind, lässt sich die Gleichung umformen in:
- [math]\displaystyle{ \frac{U_{e1}}{R_1} + \frac{U_{e2}}{R_2} = -\frac{U_a}{R_3} }[/math]
Nach Ua aufgelöst ergibt sich:
- [math]\displaystyle{ -U_a = \left (U_{e1} \cdot \frac{R_3}{R_1}\right ) + \left (U_{e2} \cdot \frac{R_3}{R_2}\right ) + ... + \left (U_{en} \cdot \frac{R_3}{R_n}\right ) }[/math]
Einen Sonderfall gibt es, wenn die Widerstände R1 und R2 gleich sind. Dann gilt
- [math]\displaystyle{ R_1 = R_2 = R_x }[/math]
und damit
- [math]\displaystyle{ -U_a = \frac{R_3}{R_x} \cdot (U_{e1} + U_{e2}) }[/math].
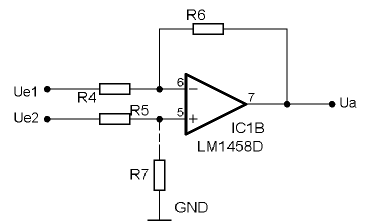
Der Subtrahierer (Differenzverstärker)
Ein Subtrahierer ist die Zusammenschaltung eines invertierenden und eines nichtinvertierenden Verstärkers. Schliessen wir Punkt Ue1 nach Masse kurz und steuern Ue2 an, arbeitet die Schaltung als nichtinvertierender Verstärker. Wird Ue2 nach Masse verbunden und Ue1 angesteuert, verhält sich die Schaltung als invertierender Verstärker (R7 vorerst nicht beachten).
Für den 1. Fall (nichtinvertierender Verstärker) gilt:
- Ua = Ue2 (1 + R6\R4 )
Für den 2. Fall (invertierender Verstärker) gilt:
- Ua = -Ue1 R6\R4
Der dritte Fall ist die Ansteuerung beider Eingänge:
- Ua = -Ue1 R6\R4 + Ue2 (1 + R6\R4 )
Diese Schaltung ist gut für eine Erklärung, praktisch aber taugt sie nichts. Denn liegen an den Eingängen gleiche Spannungen an, ist die Ausgangsspannung nicht 0, wie eigentlich zu vermuten wäre. Deshalb ändern wir die Schaltung und fügen R7 ein. Jetzt stellt sich am Punkt + des OPs die Spannung
- Ue2+ = Ue2 R7\(R5 + R7)
ein. Wenn wir das berücksichtigen, erhalten wir endlich einen richtigen Subtrahierer:
- Ua = Ue2 (1 + R6\R4 ) R7\(R5 + R7) - R6\R4 Ue1
Dies gilt für alle Subtrahierer, obwohl es natürlich auch hier wieder zwei Sonderfälle gibt; nämlich a) wenn alle Gegenkopplungswiderstände gleich sind:
- R6 = R7 = R4 = R5
dann ist
- Ua = Ue2 - Ue1
oder b) wenn die Widerstandsverhältnisse gleich sind :
- R6\R4 = R7\R5
Dann ergibt sich für Ua:
- Ua = (Ue2 R7\R5 ) - (Ue1 R6\R4 )
oder noch einfacher:
- Ua = (Ue2 -Ue1) R6\R4
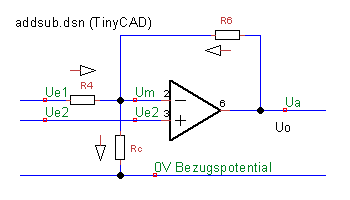
Addierer/Subtrahierer mit unterschiedlichen Faktoren
Legt man nicht den + sondern den - Eingang des Operationsverstärkers als Bezugspunkt zur Masse mit einem Widerstand fest, übernimmt der Vorwiderstand vom - Eingang, R4 die Aufgabe von R5.
Hier die Schaltung die addieren und subtrahieren kann, mit unterschiedlichen Faktoren. Sie kann verwendet werden für Aufgaben wie: Gesucht ist eine Schaltung, die aus 0...2.56 V eine Spannung von -10V...10V macht. Für dieses Beispiel wird hier die Dimensionierung durchgeführt:
| [math]\displaystyle{ U_{e1} = 5\,\mathrm{V} }[/math] | Einfach festgelegt, muss nur ein positiver Wert sein |
| [math]\displaystyle{ R_6 = 200\,\mathrm{k\Omega} }[/math] | Einfach festgelegt, könnte auch 100k oder 500k sein |
| [math]\displaystyle{ U_{e2i} = 0\,\mathrm{V},\, U_{ai} = -10\,\mathrm{V} }[/math] | gewählter momentaner Zustand 1, Ue2 = 0V ist günstig für Berechnung, Ua ist die dazupassende Ausgangsspannung |
| [math]\displaystyle{ U_{e2ii} = 2{,}56\,\mathrm{V},\, U_{aii} = 10\,\mathrm{V} }[/math] | gewählter beliebiger Zustand 2 |
| [math]\displaystyle{ U_m = U_{e2} }[/math] | Gleichgewicht am Eingang |
| [math]\displaystyle{ I_a + I_b = I_c }[/math] | In den Eingang fließt "kein" Strom |
| [math]\displaystyle{ \frac{U_a-U_{e2}}{R_6} + \frac{U_{e1}-U_{e2}}{R_4} = \frac{U_{e2}}{R_c} }[/math] | Gleichung mit den Unbekannten R4 und Rc |
| [math]\displaystyle{ \frac{U_{ai}-U_{e2i}}{R_6} + \frac{U_{e1}-U_{e2i}}{R_4} = \frac{U_{e2i}}{R_c} }[/math] | Variablen für Zustand 1 eingesetzt, bildet 1. Gleichung |
| [math]\displaystyle{ \frac{U_{aii}-U_{e2ii}}{R_6} + \frac{U_{e1}-U_{e2ii}}{R_4} = \frac{U_{e2ii}}{R_c} }[/math] | Variablen für Zustand 2 eingesetzt, bildet 2. Gleichung |
| [math]\displaystyle{ R_4=-\frac{R_6\cdot U_{e1}}{U_{ai}} }[/math] | 2 Gleichungen mit 2 Unbekannten, Lösung durch Umformen der 1. Gleichung nach R4 und einsetzen von Ue2i=0 (freundlicherweise fällt die 2. Unbekannte dabei raus) |
| [math]\displaystyle{ R_4 = 100\,\mathrm{k\Omega} }[/math] | restliche Werte eingesetzt |
| [math]\displaystyle{ R_c=\frac{R_6\cdot U_{e1}\cdot U_{e2ii}}{U_{aii}\cdot U_{e1}-U_{ai}\cdot (U_{e1}-U_{e2ii})-U_{e1}\cdot U_{e2ii}} }[/math] | Ergebnis für R4 in die 2. Gleichung einsetzen und Umformen nach Rc |
| [math]\displaystyle{ R_c = 41{,}6\,\mathrm{k\Omega} }[/math] | Werte eingesetzt |
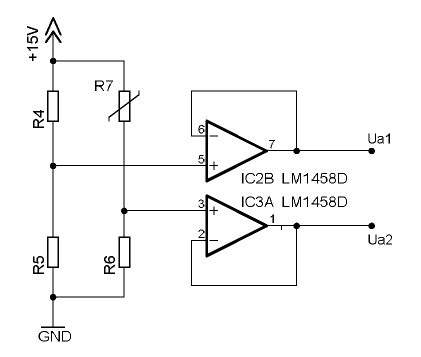
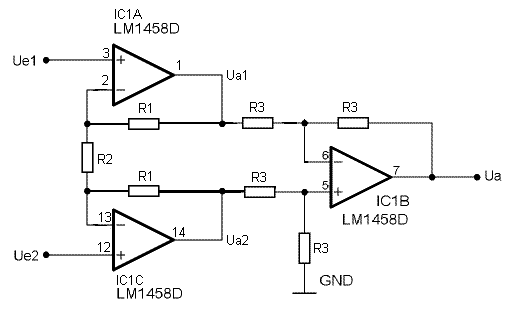
Der Instrumenten-Verstärker
Ein Nachteil des Subtrahierers ist sein geringer Eingangswiderstand. Um den nahezu unendlichen Eingangswiderstand des verwendeten Operationsverstärkers zu erreichen, kann man einfach vor beide Eingänge je einen Impedanzwandler vorschalten. Die hier beschriebene Schaltung ist um drei Widerstände erweitert und ermöglicht die Einstellung der Differenz-Verstärkung über nur einen Widerstand, nämlich R2.
Am invertierenden Eingang von IC1A gilt (Knotenregel):
- [math]\displaystyle{ \frac{U_{a1}-U_{e1}}{R_1}-\frac{U_{e1}-U_{e2}}{R_2}=0 }[/math]
Am invertierenden Eingang von IC1C gilt (Knotenregel):
- [math]\displaystyle{ \frac{U_{a2}-U_{e2}}{R_1}+\frac{U_{e1}-U_{e2}}{R_2}=0 }[/math]
Subtrahiert man die beiden Gleichungen voneinander, erhält man:
- [math]\displaystyle{ U_{a2}-U_{a1}=(U_{e2}-U_{e1})\cdot\left (1+\frac{2\cdot R_1}{R_2}\right ) }[/math]
Letztere Differenz ist die Eingangsspannung eines normalen Subtrahierers mit der Verstärkung 1.
Also ergibt sich als Ausgangsspannung:
- [math]\displaystyle{ U_a=(U_{e2}-U_{e1}) \cdot \left (1+\frac{2\cdot R_1}{R_2}\right ) }[/math]
Die Differenzverstärkung beträgt demnach:
- [math]\displaystyle{ V=\left (1+\frac{2\cdot R_1}{R_2} \right ) }[/math]
Anwendung: Auswertung von Brückenschaltungen, wie Drucksensoren oder Dehnungsmessstreifen, die durch den Eingangswiderstand der Messschaltung nicht belastet werden dürfen.
Instrumenten-Verstärker kann man auch fertig kaufen. Im INA102 ist die komplette Schaltung integriert. Für R2 sind 3 verschiedene Werte eingebaut, die bei passender Verschaltung eine Verstärkung von 1, 10, 100 oder 1000 ermöglichen.
Da die Gleichtaktunterdrückung hauptsächlich von der Übereinstimmung der Widerstände abhängt, sind für viele Standardanwendungen, insbesondere solche mit niedriger erforderlicher Bandbreite, integrierte Instrumentenverstärker zu bevorzugen.
Der Potentialdifferenzverstärker
Der Potentialdifferenzverstärker ist eine OPV-Schaltung zum gewichteten Addieren und Subtrahieren beliebiger Spannungen.
Falls die Bedingung [math]\displaystyle{ \sum\frac{R_{0}}{R_{i}}=\sum\frac{R_{0}^{'}}{R_{i}^{'}} }[/math] erfüllt ist, vereinfacht sich der Term für die Ausgangsspannung zu folgendem Term:
[math]\displaystyle{ U_{a}=\sum\frac{R_{0}^{'}}{R_{i}^{'}}U_{i}^{'}-\sum\frac{R_{0}}{R_{i}}U_{i} }[/math]
Rechenschaltungen
Der Integrator
Der Integrator wird verwendet, um die Integration eines Signales vorzunehmen. Sein Verhalten entspricht im wesentlichem der mathematischen Integration.
Der Differentiator
Der Differentiator wird verwendet, um die Differentiation (Ableitung) eines Signales vorzunehmen. Er funktioniert ähnlich wie ein Hochpass. Die Ausgangsspannung ist proportional zur Änderung der Eingangsspannung. Die Dimensionierung für eine stabile Funktion ist nicht ganz einfach, dadurch wird diese Schaltung selten verwendet.
Der Logarithmierer
Logarithmierer werden mit der Kennlinie einer Diode konstruiert, die einen eingeprägten Strom in eine Spannung übersetzt.
Potenzieren
Spannungsversorgung und Beschaltung
Betrieb mit einfacher Versorgungsspannung
Häufig möchte man eine Wechselspannung wie z.B. ein Audiosignal, das auch negative Spannungen enthält, mit einem Opamp verstärken, hat aber nur eine einfache, in Bezug zu Masse positive Versorgungsspannung zur Verfügung. Dafür bieten sich folgende Schaltungen an, die in der Literatur leider häufig vernachlässigt werden.
Durch die Kondensatoren können die Operationsverstärker in geeigneten Arbeitspunkten betrieben werden, obwohl die Eingangs- und Ausgangsspannungen echte Wechselspannungen sind. Nachteil ist die Hochpasswirkung der Kondensatoren in Verbindung mit den verwendeten Widerständen. Die Grenzfrequenz der Hochpässe muss tief genung gewählt werden, um den gewünschten Frequenzbereich verstärken zu können. Zur Verstärkung von Gleichspannungen (z.B. aus Temperatursensoren) sind diese Schaltungen nicht geeignet.
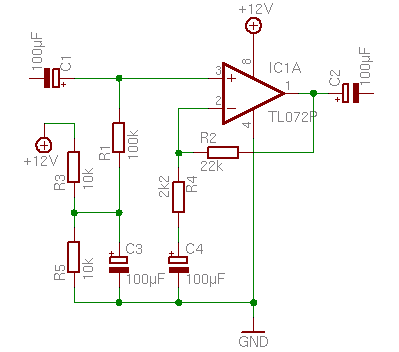
Nichtinvertierender Verstärker
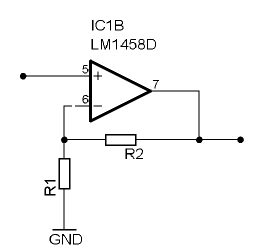
Der positive Eingang wird mit einem Spannungsteiler (R3 und R5) auf die halbe Betriebsspannung gelegt. Dieser Spannung wird dann die zu verstärkende Eingangswechselspannung überlagert. Mit den Kondensatoren am Eingang (C1) und Ausgang (C2) wird der Gleichspannungsanteil abgekoppelt.
Die Verstärkung hat in diesem Beispiel für Wechselspannung den Wert 11 (Formel wie oben), für Gleichspannung aber den Wert 1, da C4 für Gleichspannung einen unendlichen Widerstand darstellt. C3 sollte dorthin führen, wo das Eingangssignal seinen Bezugspunkt hat, also die Abschirmung der Cinch-Buchse, während R5 dorthin führt, von wo der Operationsverstärker seine negative Versorgungsspannung bekommt, falls das nicht die gleichen Potentiale, hier GND, sein sollten.
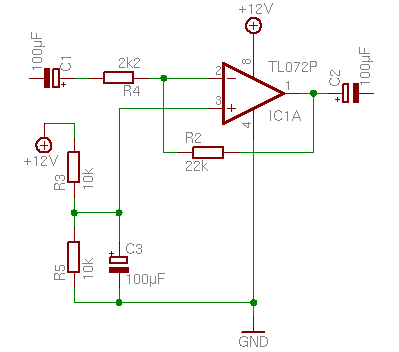
Invertierender Verstärker
Das Prinzip funktioniert analog auch für die invertierende Beschaltung:
Betrieb mit negativer Hilfsspannung
Alternativ lässt sich auch eine negative Hilfsspannung erzeugen. Damit bekommt der Operationsverstärker seine "Plus-Minus"-Versorgung, und er kann Wechselspannungen um das Ground-Potential herum problemlos verstärken.
Die negative Hilfsspannung erzeugt man zweckmässigerweise mit einer Ladungspumpe. Dazu bieten sich zwei Möglichkeiten an:
- einen speziellen IC nach der Art eines ICL 7660
- eine Rechteckspannung auf einen Spannungsverdoppler geben. Dieser besteht aus 2 Dioden und 2 Kondensatoren. Die Konfiguration sollte natürlich so sein, dass eine negative Hilfsspannung erzeugt wird. Schaltbeispiele gibt's im Netz. Als Rechteckspannung kann ein unbenutzter PWM-Ausgang dienen, der mit 50% Tastverhältnis läuft.
Ein Ripple auf der negativen Hilfsspannung wird von modernen Operationsverstärkern wirkungsvoll unterdrückt. Die PSRR (power supply rejection ratio) weist oft Werte um 120 dB auf (bei 120 Hz, darüber fällt sie meist mit 20 dB/Dekade).
Siehe auch http://de.wikipedia.org/wiki/Ladungspumpe#Negative_Ausgangsspannungen
Kaufempfehlung
LM358 2 OPs in einem Gehäuse oder LM324 4 OPs in einem Gehäuse
MCP6001/6004 CMOS OPs mit Rail to Rail Input und Output, tiefem Stromverbrauch, und geringer Versorgungsspannung
Preis jeweils ca. 0,30€ aus Deutschland oder ca. 2 bis 4 cent aus China (AliExpress, ebay, …).
Siehe auch Standardbauelemente - Operationsverstärker.
Wer Audio OpAmps sucht - tangentsoft.net hat mal welche unter die Lupe genommen: Notes on Audio OpAmps
Siehe auch
- Schmitt-Trigger
- Aktiver RC-Bandpass
- Forumsbeitrag: Pegelanpassung 0 bis 3V auf -15 bis +20V
- Forumsbeitrag: Strommessung an der Versorgungsspannung, Fehlerbetrachtung und verbesserte Schaltung
- Forumsbeitrag: "bouncing ball" Schaltung gesucht
- Forumsbeitrag: Maximum von zwei 4-20mA Eingängen auf einen 4-20mA Ausgang bilden
- Forumsbeitrag: 1500V Linearverstärker
- Forumsbeitrag: Suche OpAmp RRIO bis 36V out
- Forumsbeitrag: Sinusgenerator mit HV-Endstufe gesucht
- Forumsbeitrag: Differenzverstärker für hohe Eingangsspannungen
- Forumsbeitrag: Audioverstärker mit +/-120V Ausgangsspannung
- Forumsbeitrag: High Voltage Amplifier
Weblinks
- AN-31 - National Semiconductor Application Note 31 mit vielen weiteren OP-Schaltungen
- Op Amps for Everyone, sehr umfangreiches Dokument zu OPV und deren Anwendung, englisch
- Operationsverstärker im ElKo
- OP Teil 1, OP Teil 2 - OP-Schaltungen (deutsch)
- RN-Wissen Operationsverstärker
- Online Seminar von National Semiconductor
- ELO-Online-Magazin, Franzis-Verlag, Lernpaket Elektronik mit ICs "Elektronische Experimente mit integriertem Schaltkreis", Kasten mit Steckbrett/Bauelementen (ca. 40EUR),
- OpAmp Praxis, Praktikertipps + schwingende Operationsverstärker in den Griff bekommen
- Frequenzvervielfacher
- Präzisionsgleichrichter, engl.
- ElektroEasy-App, Berechnung von OPVs
- Grundlagen Operationsverstärker
- Rauschverhalten von OpAmps
- Class AB inverting amp uses two floating-amplifier cells, HV-Verstärker mit +/-500V Ausgangsspannung
- A deeper insight into Differential Amplifiers with high common mode voltage, Youtube-Video
- Rinck Electronics GmbH, Messtechnik - Stromversorgung - Anzeigen - Handbedienebenen
- TSP #246 - High-Voltage Amplification, Signal Generation, Power Supply Design Tutorial & Experiments
- PID Regler einstellen
- The Bob Pease Show, Youtube Playlist
- Was macht ein PID-Regler? Youtube Video (engl.)