Stromwandler

Aus der Mikrocontroller.net Artikelsammlung, mit Beiträgen verschiedener Autoren (siehe Versionsgeschichte)
Wechseln zu: Navigation, Suche

Ein Stromwandler ist ein Transformator, welcher zur galvanisch getrennten Messung von Strömen verwendet wird.

Aufbau und Funktion

Passive Stromwandler

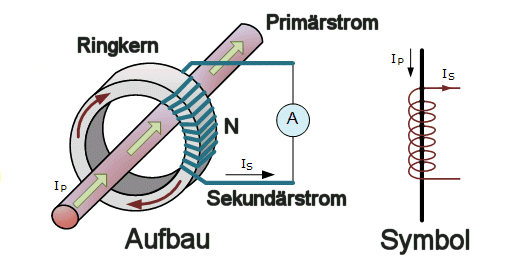
Ein passiver Stromwandler besteht dem Prinzip nach aus einem Transformator. Meist ist dieser als Ringkern ausgeführt. Durch das Loch des Ringkerns wird das Kabel des zu messenden Stroms geführt und bildet die Primärwicklung mit einer Windung. Auf dem Ringkern befindet sich die Sekundärwicklung mit ca. 100–1000 Windungen. Die Sekundärwicklung ist immer mit einem niederohmigen Messwiderstand (Bürdewiderstand) im englischen meist als shunt (Umleitung) abgeschlossen; typische Werte liegen bei 10Ω–200Ω. Andere Bauformen sind als gewundene Stromschienen realisiert, welche mit Wicklungen versehen sind, oder einen Shunt enthalten.

Stromwandler.png

Am stärksten sind die elektromagnetischen Stromwandler verbreitet, weil diese eine galvanische Trennung bieten. Sie funktionieren wie Übertrager, haben aber naturgemäß etwas exotische Werte, was das Verständnis bisweilen erschwert. Zum einen ist die Ausgangsspannung der Sekundärseite recht niedrig, typisch 0,5V–2V. Zum anderen ist der Eingangsstrom recht hoch, von wenigen Ampere bis in den Bereich von Kiloampere, was oftmals der Grund für den Einsatz solcher Wanderl ist. Dabei wird der Strom gemäß der bekannten Trafoformel im Verhältnis der Windungszahlen heruntertransformiert:

[math]\displaystyle{ I_S=\frac{I_P}{N} }[/math]
  • [math]\displaystyle{ I_S }[/math] : Sekundärstrom
  • [math]\displaystyle{ I_P }[/math] : Primärstrom
  • [math]\displaystyle{ N }[/math] : Windungszahl des Sekundärwicklung

Das gilt allerdings nur, wenn der Belastungswiderstand nicht zu hochohmig ist und der Wandler nicht etwa durch einen zu großen Eingangsstrom in die Sättigung gerät. Da es sich um einen normalen Trafo handelt, kann er nur Wechselströme transformieren. Die untere und obere Grenzfrequenz ist vom Kernmaterial und dem Aufbau abhängig. Typischerweise gibt es Stromwandler für Netzanwendungen mit 50/60Hz sowie für Schaltnetzteile im Bereich 20kHz–500kHz.

Ein Stromwandler wirkt praktisch immer wie eine Konstantstromquelle, zumindest solange er nicht in die Sättigung geht. D.h. man kann z.B. einen Brückengleichrichter direkt anschließen und dahinter ein Gleichstrommessgerät. Der Spannungsabfall der Dioden spielt dabei keine Rolle, ein Präzisionsgleichrichter mit Operationsverstärkern ist nicht notwendig. Allerdings darf er nicht dazu führen, dass die Ausgangsspannung zu stark ansteigt, weil dann wieder Sättigung droht.

Will man die Empfindlichkeit eines Stromwandlers erhöhen, kann man die Leitung der Primärseite mehrfach durch den Ringkern führen, soweit das mechanisch möglich ist. Damit vervielfacht man die Empfindlichkeit um den Faktor M, der Primärwindungszahl. Der Preis dafür ist, dass der Messbereich auch um den Faktor 1/M kleiner wird.

Aktive Stromwandler

Viele aktive Stromwandler basieren ebenfalls auf einem Ringkern. Allerdings misst er das Magnetfeld des Kabels nicht per Sekundärspule, sondern z.B. mit einem Hallsensor, welcher in einen Schlitz des Ringkerns eingefügt wurde. Mit dieser Anordnung lassen sich auch Gleichströme messen. Der Nachteil ist der höhere Aufwand und damit Preis sowie die Notwendigkeit einer Stromversorgung. Oftmals benötigen die Hall-Sensoren auch einen Verstärker, um sehr kleine Werte erfassen zu können. Ein anderes Messprinzip sind sogenannte Kompensationsstromsensoren, bei denen ein magnetisches Material wechselseitig umgepolt wird, um es in einem Gleichgewicht zu halten, welches durch die äußere Anregung des Primärstroms gestört wird, wodurch es messbar wird.

Typen für besonders kleine Ströme werden oft auch als Stromsensoren bezeichnet. Mit aktiven Typen auf Hallsensor- oder Magnetsensorbasis sind Messgenauigkeiten bis 0,2% und bis mehrere 10kHz erreichbar. Mit halbpassiven Typen, bestehend aus shunt und Messverstärker sind sehr viel höhere Bandbreiten, aber bei geringen Strömen nur geringe Genauigkeiten zu erzielen. Auch eignen sich diese nicht für sehr hohe Ströme.

Stromzange

Eine Stromzange ist ähnlich einem Stromwandler aufgebaut, nur dass der Ringkern aufklappbar ist, um ein Kabel durchführen zu können. Je nach Typ (aktiv oder passiv) können Stromzangen entweder nur Wechselstrom oder auch Gleichstrom messen. Es existieren Ausführungen als standalone-Gerät mit eigener Stromverorung sowie Ausführungen als Vorsatz für Digitalmultimeter.

Beispiel-Auslegung

Hier folgt eine beispielhafte Berechnung eines elektromagnetischen Stromwandlers:

Im Prinzip berechnet sich ein Stromwandler wie ein normaler Trafo. Prinzipiell kann man die Berechnung von der Primär- als auch Sekundärseite vornehmen. In der Praxis ist die Sekundärseite von Vorteil, weil hier fast alle wichtigen Parameter direkt vorgegeben und berechnet werden können.

Windungszahl

Zunächst muss man festlegen, wie groß die Windungszahl N sein soll, denn sie legt das Übersetzungsverhältnis fest. Will man große Ströme messen, braucht man meist viele Windungen, da man ja möglichst kleine, handhabbare Ströme auf der Sekundärseite haben möchte.

Ausgangsspannung

Der Shunt legt fest, wieviel Ausgangsspanung direkt zur Verfügung steht. Zum einen ist eine hohe Ausgangsspannung wünschenswert, um möglichst ohne Verstärkung eine Auswerteschaltung wie z.B. einen Gleichrichter oder AD-Wandler speisen zu können. Andererseits benötigt man für hohe Ausgangsspannungen einen relativ großen Kern mit großem Querschnitt. Der Zusammenhang zwischen Eingangsstrom, Ausgangsspannung und Shunt ist denkbar einfach.

[math]\displaystyle{ U_A = \frac{I_E}{N} \cdot R_S }[/math]
  • [math]\displaystyle{ R_S }[/math] : Messwiderstand
  • [math]\displaystyle{ U_A }[/math] : Ausgangsspannung, Effektivwert
  • [math]\displaystyle{ I_E }[/math] : Eingangsstrom, Effektivwert

Kerngröße

Der Kern muss genügend Querschnitt haben, um bei der gewählten Windungszahl und Ausgangsspannung nicht in die Sättigung zu gehen. Die grundlegende Trafoformel gibt hier einfach und schnell eine Antwort. Dazu muss man jedoch wissen, wieviel Flussdichte das jeweilige Material verträgt. Diesen Wert findet man im Datenblatt. Ist das nicht verfügbar kann man von Standardwerten ausgehen (Ferrit ca. 0,3T, Eisenpulver ca. 0,5T, Trafoeisen ca. 1,5T)

[math]\displaystyle{ N = \frac{U_A}{4,44 \cdot f \cdot A \cdot B} }[/math]
  • f: Frequenz (Formel gilt für Sinussignale)
  • [math]\displaystyle{ A }[/math] : Magnetischer Querschnitt des Kerns
  • [math]\displaystyle{ B }[/math] : Magnetische Flußdichte

Das ist die minimale Anzahl von Windungen, die der Kern mit diesem Querschnitt benötigt. Mehr schaden nicht, bei weniger geht der Kern bei voller Aussteuerung in die Sättigung. Will man dennoch einen kleinen Kern nutzen, muss man die Ausgangspannung verringern, d.h. einen kleineren Shunt wählen. Möchte man einen sehr kleinen Shunt nutzen, ist es meist sinnvoll einen Transimpedanzverstärker zu nutzen. Dieser hat einen Eingangswiderstand von praktisch Null Ohm. Dabei darf man aber nicht den ohmschen Widerstand der Sekundärwicklung vergessen, dieser kann mehrere Dutzend Ohm betragen, besonders bei kleinen Stromwandlern mit sehr vielen Windungen. Dieser wirkt dann als Grenze für das Absenken des Shuntwiderstands.

Kernmaterial

Das Kernmaterial bestimmt die Induktivität unseres Trafos. Auch hier gilt, dass für niedrige Frequenzen eine sehr hohe Induktivität nötig ist, um den Magnetisierungsstrom klein zu halten. Denn dieser fließt zusätzlich zum Messtrom und verfälscht dabei das Messergebnis. Die Induktivität kann man leicht ausrechnen.

[math]\displaystyle{ L = A_L \cdot N^2 }[/math]

Der [math]\displaystyle{ A_L }[/math]-Wert ist im Datenblatt des Ringkerns angegeben, beim Recycling von Ringkernen muss man ihn messen, siehe Artikel Spule. Mit Hilfe der Induktivität kann man ebenso leicht den Blindwiderstand bei der Arbeitsfrequenz berechnen und über die Ausgangsspannung den Blindstrom (Magnetisierungsstrom).

[math]\displaystyle{ X_L = 2 \cdot \pi \cdot f \cdot L }[/math]
[math]\displaystyle{ I_M = \frac{U_A}{X_L} }[/math]

Beachten muss man dabei, dass Messstrom und Magnetisierungsstrom um 90 Grad phasenverschoben sind, d.h. sie müssen geometrisch addiert werden (Komplexe Zahlen, Zeigerdiagramm). D.h. jedoch, dass selbst ein Magnetisierungsstrom von 10% sich nur als ca. 5% Gesamtfehler auswirkt.

[math]\displaystyle{ F_M = ( \frac{\sqrt {I_M^2+I_A^2}}{I_A}-1 ) \cdot 100\% }[/math]
  • [math]\displaystyle{ F_M }[/math]: Messfehler

Bei höheren Frequenzen im kHz-Bereich wird man auf geringere Permeabilitäten zurückgreifen, das wirkt sich auch günstig auf die Verringerung der Streuinduktivitäten aus und erhöht damit die obere Grenzfrequenz auf Kosten der unteren Grenzfrequenz.

Beispiel

Nehmen wir an, wir wollen einen Stromwandler für 50 Hz Netzstrom selber entwickeln. Nennstrom sollen 16A sein, das ist der Maximalwert, den man einer normalen Steckdose entnehmen kann. Als Ausgangsspannung wollen wir 2V erhalten, beide Werte sind Effektivwerte. Als brauchbaren Ringkern wollen wir den Typ TN20/10/7-3E25 von Ferroxcube nutzen, er hat 9mm Innendurchmesser, einen Querschnitt von 33,6mm2 und einen [math]\displaystyle{ A_L }[/math]-Wert von 5340 nH/N². Es ist ein Ferritkern, auch wenn diese in der Praxis eher nicht für 50 Hz Wandler genutzt werden.

Die minimale Windungszahl berechnet sich aus.

[math]\displaystyle{ \begin{align} N &= \frac{U}{4,44 \cdot f \cdot A \cdot B} = \frac{2\text{V}}{4,44 \cdot 50 \cdot 33,6\cdot 10^{-6}\text{m}^2 \cdot 0,3\text{T}} = 893 \end{align} }[/math]

Somit entscheiden wir uns für 1000 Windungen, das vereinfacht die Berechung. Diese Wicklung hat einen nenneswerten, ohmschen Widerstand, der berücksichtig werden muss. Der Querschnittsumfang des Ringkerns beträgt hier ca. 27mm, ergibt bei 1000 Windungen 27m Drahtlänge. Nutzt man dafür 0,15mm dicken Kupferlackdraht (CuL), so hat dieser einen Widerstand von ca.

[math]\displaystyle{ R_{WS} = \frac{\rho \cdot l}{A} = \frac{18m \frac{\Omega \cdot mm^2}{m} \cdot 27m}{0,018mm^2} = 27 \Omega }[/math]

Daraus ergibt sich unser Shuntwiderstand zu

[math]\displaystyle{ \begin{align} R_S &= \frac{U_A \cdot N}{I_E} - R_{WS} = \frac{2\text{V} \cdot 1000}{16\text{A}} - 27 \Omega = 98\Omega \end{align} }[/math]

Wir wählen den Normwert 91Ω.

Zum Schluss prüfen wir den Fehler durch den Blindstrom.

[math]\displaystyle{ \begin{align} L &= A_L \cdot N^2 = 5340 \frac {nH}{N^2} \cdot 1000^2 = 5,34H \end{align} }[/math]

5,3 H sind sehr viel.

[math]\displaystyle{ \begin{align} X_L &= 2 \cdot \pi \cdot f \cdot L = 2 \cdot \pi \cdot 50\text{Hz} \cdot 5,34\text{H} = 1677\Omega \end{align} }[/math]
[math]\displaystyle{ \begin{align} G_L = \frac {1}{X_L} = \frac {1}{1677 \Omega} = 0,59 mS \end{align} }[/math]
[math]\displaystyle{ \begin{align} G = \frac {1}{R_S + R_{WS}} = \frac {1}{91 \Omega + 27 \Omega} = 8,5 mS \end{align} }[/math]
[math]\displaystyle{ \begin{align} F_M &= \frac{G_L}{\sqrt{G_L^2+G^2}} \cdot 100 \text % = \frac{0,59 mS}{\sqrt{{0,59 mS}^2+{8,5 mS}^2}} \cdot 100 \text % = 6,9 \text % \end{align} }[/math]

Anwendungen

  • Messwandler für hohe bis sehr hohe Ströme (Schweißgeräte, Ladegeräte, Fahrzeugbatterien)
  • Messwandler für hohe Spannungsisolation (Hochspannungsnetze)
  • Messwandler in Schaltnetzteilen (hohe Frequenzen)
  • Stromzangen (mobile Messungen, Hausinstallation)
  • Fehlerstromschalter (FI-Schalter, kleine Ströme)
  • Kontaktloses Messen (durch Wände und Isolationn)

Siehe auch

Weblinks

  • Stromwandler und Stromsensor bei Wikipedia
  • LEM, bekannter Hersteller von aktiven Stromwandlern
  • VAC Hersteller von Kompensationsstromsensoren
  • Allegromicro, ein anderer bekannter Hersteller von aktiven Stromwandlern.
Abgerufen von „https://www.mikrocontroller.net/index.php?title=Stromwandler&oldid=105333“