www.mikrocontroller.net

Pulsweitenmodulation

Inhaltsverzeichnis

1 Einleitung
2 Beispiele
3 Leistung
- 3.1 Beispiel
4 Anwendung
5 Siehe auch

[bearbeiten] Einleitung

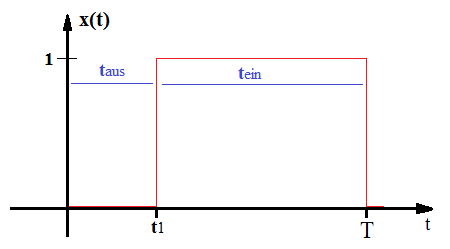
Bei der Pulsweitenmodulation (engl. Pulse Width Modulation, abgekürzt PWM) wird die Ein- und Ausschaltzeit eines Rechtecksignals bei fester Grundfrequenz variiert. Das Verhältnis $t e i n / (t e i n + t a u s)$ bezeichnet man als Tastverhältnis (engl. Duty Cycle, meist abgekürzt DC, bitte nicht verwechseln mit Direct Current = Gleichstrom ). Das Tastverhältnis ist eine Zahl zwischen 0..1.

Wie leicht zu erkennen ist gilt für den Mittelwert der Spannung:

$U_m = U_{aus} + (U_{ein} - U_{aus}) \cdot \frac{t_{ein}}{t_{ein}+t_{aus}}$

$U a u s$ ist dabei normalerweise 0V, $U e i n$ die Betriebsspannung $V C C$ , z.B. 5V. Deshalb kann man vereinfacht schreiben:

$U_m = V_{CC} \cdot DC$ .

[bearbeiten] Beispiele

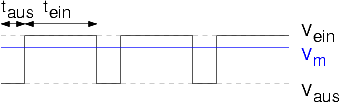
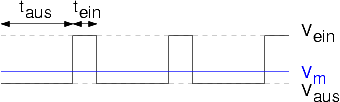
Die folgenden Beispiele zeigen PWM-Signale mit einem Tastverhältnis von 75% bzw. 25%.

Beispiel 1

$U_{ein}=5\,\mathrm{V}$
$U_{aus}=0\,\mathrm{V}$
$t_{ein}=3\,\mathrm{ms}$
$t_{aus}=1\,\mathrm{ms}$

$U_m = 0\,\mathrm{V} + (5\,\mathrm{V} - 0\,\mathrm{V}) \cdot \frac{3\,\mathrm{ms}}{3\,\mathrm{ms}+1\,\mathrm{ms}} = 3,75\,\mathrm{V}$

Beispiel 2

$U_{ein}=5\,\mathrm{V}$
$U_{aus}=0\,\mathrm{V}$
$t_{ein}=1\,\mathrm{ms}$
$t_{aus}=3\,\mathrm{ms}$

$U_m = 0\,\mathrm{V} + (5\,\mathrm{V} - 0\,\mathrm{V}) \cdot \frac{1\,\mathrm{ms}}{1\,\mathrm{ms}+3\,\mathrm{ms}} = 1,25\,\mathrm{V}$

[bearbeiten] Leistung

Steuert man mit einem pulsweitenmodulierten Signal direkt einen ohmschen Verbraucher an (z.B. Heizdraht), so ist darauf zu achten, dass man zur Bestimmung der Leistung nicht einfach

$P = \frac{{U_m}^2}{R}$

rechnen darf, sondern die Leistung während der Ein- und Ausschaltzeit getrennt betrachten muss:

$P = \frac{{U_{ein}}^2}{R} \cdot \frac{t_{ein}}{t_{ein} + t_{aus}} + \frac{{U_{aus}}^2}{R} \cdot \frac{t_{aus}}{t_{ein} + t_{aus}}$ .

Da praktisch fast immer gilt $U a u s = 0 V$ sowie $U e i n = V C C$

kann man vereinfacht schreiben und damit rechnen.

$P = \frac {{V_{CC}}^2}{R} \cdot DC$ .

[bearbeiten] Beispiel

$U_{ein} = 4\,\mathrm{V}$
$U_{aus} = 0\,\mathrm{V}$
$t_{ein} = 1\,\mathrm{ms}$
$t_{aus} = 3\,\mathrm{ms}$
$R = 10\,\mathrm{\Omega}$

Der Mittelwert dieser Spannung ist

$U_m = 1\,\mathrm{V}$ .

Würde man mit diesem Wert die Leistung berechnen, so käme man auf

$P = \frac{{U_m}^2}{R} = \frac{(1\,\mathrm{V})^2}{10\,\mathrm{\Omega}} = 0,1\,\mathrm{W}$ .

Der richtige Wert ist jedoch

$P = \frac{(4\,\mathrm{V})^2}{10\,\mathrm{\Omega}} \cdot \frac{1\,\mathrm{ms}}{4\,\mathrm{ms}} + \frac{(0\,\mathrm{V})^2}{10\,\mathrm{\Omega}} \cdot \frac{3\,\mathrm{ms}}{4\,\mathrm{ms}} = 0,4\,\mathrm{W}$ .

[bearbeiten] Anwendung

Beispiel:

Eine Heizung mit 10Ohm-Widerstand soll mit bis zu 12V angesteuert werden. Dazu wird ein 13V-Netzteil sowie ein linearer Verstärker verwendet (ein linearer Verstärker braucht immer eine etwas höhere Betriebsspannung als die maximale Ausgangsspannung). Sollen nun 12V auf die Heizung gegeben werden, fällt (fast) die gesamte Spannung über der Heizung selber ab, der Verstärker "verbraucht" nur 1V. Es fliessen ca. 1,2A, es werden ca. 14,4W in der Heizung in Wärme umgesetzt, im Verstärker ca. 1,2W, der Wirkungsgrad beträgt 92%. Wenn jetzt aber nur noch 6V an der Heizung anliegen sollen, muss der lineare Verstärker die "übrigen" 7V verbrauchen, d.h. von den 13V, welche konstant vom Netzteil geliefert werden, fallen 7V über dem Verstärker und 6V über der Heizung ab. Die Transistoren des linearen Verstärkers sind nur halb durchgesteuert. Es fliesst ein Strom von ca. 600mA, in der Heizung werden ca. 3,6W in Wärme umgesetzt. Allerdings werden auch 4,2W im Verstärker in Wärme umgesetzt!
Der Wirkungsgrad ist nur noch 46%!

Im Gegensatz dazu sind bei einer PWM die Transistoren des digitalen Verstärkers immer nur entweder voll durchgesteuert oder gar nicht durchgesteuert. Im ersteren Fall fällt nur eine geringe Verlustleistung über dem Transistor ab, da die Sättigungsspannung $V S A T$ sehr gering ist (meist weniger als 1V). Im zweiten Fall fällt gar keine Verlustleistung über dem Transistor ab, da kein Strom fliesst (P=U*I). Im Fall der 6V an der Heizung beträgt das notwendige Tastverhältnis 0,23. D.h. nur während 23% der PWM-Periode wird Verlustleistung im digitalen Verstärker erzeugt und zwar ca.

$P_V=DC \cdot \frac {V_{CC}}{R} \cdot V_{SAT} = 0,23 \cdot \frac {12V}{10\Omega} \cdot 1V = 0,28W$

Der Wirkungsgrad liegt bei 92%!

[bearbeiten] Motorsteuerung

Eine der Hauptanwendungen für PWM ist die Ansteuerung von (Gleichstrom-) Motoren. Der große Vorteil von PWM ist hier der gute Wirkungsgrad. Würde man einen Digital-Analog-Wandler mit einem nachgeschalteten analogen Verstärker zur Ansteuerung verwenden, dann würde im Verstärker eine sehr hohe Verlustleistung in Wärme umgewandelt werden. Ein digitaler Verstärker mit PWM hat dagegen sehr geringe Verluste. Die verwendete Frequenz liegt meist im Bereich von einigen 10kHz. Zur Berechnung der Drehzahl eines Motors kann im Normalfall der Mittelwert der PWM-Spannung als Betriebsspannung angenommen werden.

[bearbeiten] AD-Wandlung mit PWM

Einen recht billigen und einfachen AD-Wandler mit "1-Draht Kommunikation" kann man mit dem IC 556 (NE556 o.ä.) realisieren: der eine Timer des 556 arbeitet als 50% duty-cycle Rechteckgenerator bei beispielsweise 1 kHz und steuert den zweiten Timer an. Dieser besitzt einen Steuereingang zu Beeinflussung des Tastverhältnisses und auf diesen Pin gibt man das analoge Signal. Ein angeschlossener µC oder PC misst bei jedem Impuls die Impulslänge und man erhält so das Messergebnis. Bei >10 kHz kann man so auch prima digital Sprache übertragen oder speichern (Tip stammt noch aus der Zeit als es keinen Mikroprozessor mit AD-Wandler gab.). Allerdings gibt es auch heute noch einige Controller ohne AD-Wandler.

[bearbeiten] DA-Wandlung mit PWM

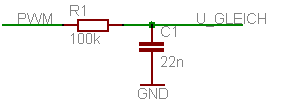
Die meisten Mikrocontroller haben keine DA-Wandler integriert, da diese relativ aufwändig sind. Allerdings kann man mittels eines PWM-Ausgangs auch eine DA-Wandlung vornehmen und eine Gleichspannung bereitstellen. Wird ein PWM-Signal über einen Tiefpass gefiltert (geglättet), entsteht eine Gleichspannung mit Wechselanteil, deren Mittelwert dem des PWM-Signals entspricht und dessen Wechselanteil von der Beschaltung abhängig ist. Nun bleibt das Problem der Dimensionierung des Tiefpasses. Ein Beispiel:

PWM-Takt 1 MHz, 8 Bit Auflösung (256 Stufen), 0/5V. -> 3906 Hz PWM Frequenz

RC-Tiefpass 22nF, 100kΩ -> 72 Hz Grenzfrequenz

Bei diesem Tiefpass mit 72 Hz Bandbreite verbleibt am Ausgang noch ein Ripple auf der Gleichspannung, da die PWM nie ideal gefiltert werden kann. Eine Rechnung bzw. Simulation in PSPICE zeigen ca. 150mV Ripple. Das ist ziemlich viel, da ein idealer 8-Bit DA-Wandler bei 5V Referenzspannung eine Auflösung von 20mV hat. Wir haben hier also ein Störsignal von 150mV/20mv=7,5 LSB. Um den Ripple bis auf die Auflösungsgrenze von 20mV zu reduzieren, muss die Grenzfrequenz auf ca. 10 Hz reduziert werden. Es ist somit effektiv nur ein 390tel der PWM-Frequenz nutzbar. Das ist für einige Anwendungen ausreichend, wo praktisch nur statische Gleichspannungen erzeugt werden sollen, z.B. für programierbare Netzteile. Für Applikationen, in denen schneller ändernde Gleichspannungen generiert werden sollen, muss die Grundfrequenz entsprchend erhöht werden.

Allgemein kann man den Ripple eines einfachen RC-Tiefpasses so abschätzen:

Kritischster Punkt ist eine PWM mit 50% Duty Cycle. Das macht den stärksten absoluten Ripple. Dort liegt 1/2 VCC über dem R an und lädt C annähernd mit Konstantstrom.

$I = \frac{\frac{1}{2}Vcc}{R}$

Über die Definition des Kondensators kann man den Ripple berechnen.

$C = \frac{As}{V}$

$V = \frac{As}{C}$

Die Ladung in As (Amperesekunden) ergeben sich aus der halben PWM-Periode mal I. Damit kann man brauchbar den Ripple abschätzen.

$V_{Ripple} = \frac{\frac {\frac{1}{2}Vcc}{R} \cdot \frac{1}{2}T_{PWM}}{C} = \frac{ Vcc \cdot T_{PWM}}{4RC}$

Die Einschwingzeit des Signals t_s bei einem neuen PWM-Wert ist in etwa 5RC.

Die Abschätzung gilt aber nur dann, wenn der Ausgang des RC-Filter kaum belastet ist, wie z.B. durch einen Operationsverstärker oder einen andern hochohmigen IC-Eingang.

Beispiel:

100 Hz PWM Frequenz(T_PWM=10ms), R=100kΩ, C=1μF, Vcc=5V

$V_{Ripple} = \frac{5V \cdot 10ms}{4 \cdot 100k\Omega \cdot 1 \mu F} = 125 mV$

$t_s=5RC=5 \cdot 100k \Omega \cdot 1 \mu F = 500ms$

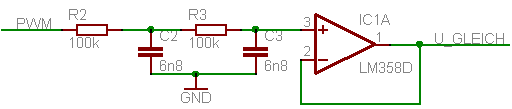
Will man aber nicht soviel Bandbreite verschenken, muss man anders filtern. Das Problem des einfachen RC-Tiefpasses ist der relativ langsame Anstieg der Dämpfung oberhalb der Grenzfrequenz. Genauer gesagt steigt die Dämpfung mit 20dB/Dekade. Das heisst, dass ein Signal mit der 10fachen Frequenz (Dekade) um den Faktor 10 (20dB) gedämpft wird. Will man nun eine höhere Dämpfung ereichen, müssen mehrere Tiefpässe in Kette geschaltet werden. Bei dem gleichen Beispiel erreicht man mit zwei Tiefpässen mit 6,8nF/100kΩ eine Grenzfrequenz von ca. 70 Hz, bei gleicher Dämpfung des Ripples auf 20mV. Die Dämpfung dieses sogenannten Tiefpasses 2. Ordnung beträgt 40dB/Dekade. Das heisst, ein Signal mit zehnfacher Frequenz (Dekade) wird um den Faktor 100 (40dB) gedämpft! Damit erzielt man hier bereits die 7fache Bandbreite! Zum Schluss muss beachtet werden, dass die passiven Tiefpässe nur sehr schwach belastet werden können. Hier ist fast immer ein Operationsverstärker als Spannungsfolger nötig. Der kann auch genutzt werden, um das gefilterte Signal weiter zu verstärken (nichtinvertierender Verstärker).

Das Spiel kann noch um einiges gesteigt werden, wenn man Tiefpässe dritter, vierter und noch höherer Ordung einsetzt. Das wird vor allem im Audiobereich gemacht. Dazu werden praktisch Operationsverstärker eingesetzt. In der AVR Application-Note AVR335: Digital Sound Recorder with AVR and DataFlash wird zum Beispiel ein mit Operationsverstärkern aufgebauter Chebychev-Tiefpass fünfter Ordnung verwendet. Man findet im Audiobereich gelegentlich auch Schaltungen ohne expliziten Tiefpass. Dabei wird der Ausgang eines Class-D Verstärkers (der nichts anderes als ein PWM-Signal erzeugt) über einen Widerstand auf einen Lautsprecher gegeben. Die mechanische Trägheit und die Induktivität der Lautsprecherspule bilden mit dem Widerstand einen Tiefpass.

[bearbeiten] Siehe auch

AVR-Tutorial: PWM
AVR-GCC-Tutorial: PWM
Soft-PWM - PWM in Software
LED-Fading - LED dimmen mit PWM
AVR PWM (noch nicht fertig)

Von „http://www.mikrocontroller.net/articles/Pulsweitenmodulation“