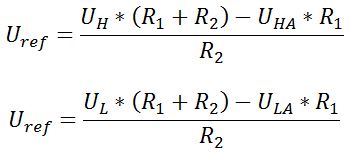Schmitt-Trigger

Einleitung

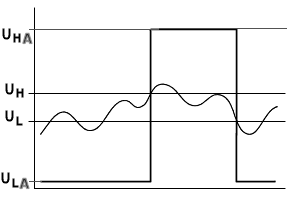
Der Schmitt-Trigger bezeichnet eine elementare Komparatorschaltung der Elektrotechnik, welche es ermöglicht den einen Spannungspegel für das Umschalten zu High 1 und zu Low 0, in zwei gegeneinander verschobene Schaltschwellen zu separieren. Der damit entstandene Spannungsbereich zwischen den neuen Schaltschwellen, führt zu einer Hysterese. Ein Schmitt-Trigger ist an vielen Eingängen von Mikrochips zu finden. Die Schaltung besitzt einen Eingang und einen Ausgang und liefert abhängig vom Eingangspegel und dessen Verlauf immer einen wohl definierten Ausgangspegel. Dabei gilt stets:

Beispiel

• Am Ausgang liegt HIGH an, wenn der Pegel am Eingang eine Spannung U_H überschreitet.
• Am Ausgang liegt LOW an, wenn der Pegel am Eingang eine Spannung U_L unterschreitet.
• Dabei wird der bisherige Ausgangspegel aufrechterhalten, wenn sich der Eingangspegel zwischen U_L und U_H befindet (Hysterese)
• Der Übergang von LOW auf HIGH bzw. von HIGH auf LOW erfolgt stets mit steiler Flanke.

Es ist demnach von Relevanz aus welcher Richtung das Signal kommt, wenn dessen Pegel in den Mittenbereich gerät. Durch die Hysterese ist sichergestellt, dass es im Grenzbereich nicht zu einem flatternden Umschalten kommen kann. Dieses Verhalten wird in der Praxis beispielsweise ausgenutzt, um ein verrauschtes Digitalsignal wieder "aufzufrischen" indem verhindert wird, dass kleine Signalschwankungen zu einem Umschalten und einem quasi Prellen des Ausgangs führen.

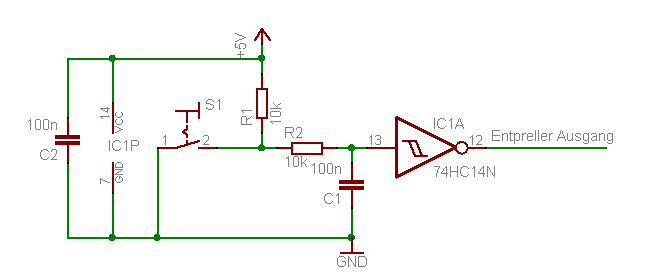
Der Hysteresebereich ist vergleichsweise eng begrenzt und kann nur eine definiertes Schwankungsbreite abfangen. Daher müssen mechanische Taster bzw. Relaiskontakte zusätzlich entprellt werden, wenn sie digitale ICs ansteuern sollen. Dies gilt gerade bei einer Generierung von sauberen Taktsignalen. Dafür wird gerne ein Tiefpassfilter verwendet, welcher das Schaltsignal vor dem Schmitt-Trigger Eingang filtert, wodurch unerwünschte Prellimpulse mit hoher Amplitude entfernt werden und das Nutzsignal klarer definiert ist. Das Ziel wäre in diesem Fall die Reduzierung der Amplitudenschwankung auf den Bereich, den der Schmitttrigger noch verarbeiten kann. Idealerweise liegt der Prellbereich deutlich ober- oder unterhalb des Hysteresebereiches. Dies lässt sich dadurch erreichen, dass die Entprellschaltung eine Diode über dem Ladekondensator hat, welche diesen in einer Richtung schneller entlädt, als in der anderen.

Integrierte Schmitt-Trigger

Es existieren fertige ICs mit Schmitt-Trigger-Funktionalität. In der 74xx-Reihe ist das beispielsweise der 74xx14, weitere Typen sind im Artikel 74xx aufgeführt. In der 4000er-Serie gibt es die Typen 4093 und 40106. Viele Mikrocontroller wie z. B. der AVR haben bereits Schmitt-Trigger Eingänge, sodass nur noch die beiden Widerstände und der Kondensator benötigt werden. Der Vorteil dieser Schmitt-Trigger ist, daß sie ohne weitere Beschaltung direkt nutzbar und auch sehr schnell sind. Der Nachteil sind die eher ungenauen Schaltschwellen. Manchmal kann man auch einen Schmitt-Trigger aus einem überzähligem, nicht invertierendem Gatter bauen.

Taster entprellen mit 74HC14

• Forumsbeitrag: Klassischer Pulsverdoppler mit XOR-Gatter und RC-Glied + Schmitt-Trigger

Schmitt-Trigger mit Operationsverstärker oder Komparator

Ein Schmitt-Trigger lässt sich auch mit Hilfe eines Operationsverstärkers oder besser eines Komparators aufbauen. Komparatoren sind im Vergleich zu OPVs deutlich schneller. Man sollte sie immer nur als Komparatoren benutzen und nicht als lineare Verstärker. OPVs sollte man nur als Komparatoren beschalten, wenn es nicht um höchste Schaltgeschwindigkeiten geht.

Nichtinvertierender Schmitt-Trigger

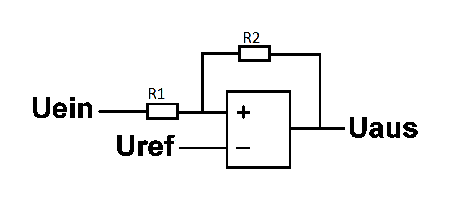
Nichtinvertierender Schmitt-Trigger

Am - Eingang des OPV wird die Referenzspannung angelegt. Achtung! Diese liegt im allgemeinen NICHT mittig zwischen den beiden Schaltschwellen. R2 sorgt für die Mitkopplung und damit für die Hysterese. Über das Verhältnis von R1/R2 wird die Hysteresebreite festgelegt. Wird also U_H am Eingang überschritten, geht der Operationsverstärker in die positive Sättigung U_HA, wird U_L unterschritten, geht er in die negative Sättigung U_LA.

[math]\displaystyle{ U_{ref}=U_{LA} + (U_H - U_{LA} ) \frac{R_2}{R_1 + R_2} }[/math]

[math]\displaystyle{ U_{ref}=U_{L} + (U_{HA}-U_L) \frac{R_1}{R_1 + R_2} }[/math]

Durch Gleichsetzen und Umformen der beiden Gleichungen kann man R2 berechnen, wobei R1 vorher festgelegt werden muss.

[math]\displaystyle{ R_2=R_1 \cdot \frac{U_{HA}-U_{LA}}{U_H - U_L} }[/math]

Durch Einsetzen in die 1. oder 2. Gleichung kann man abschließend U_ref berechnen. Die Referenzspannung kann man direkt aus einer Spannungsreferenz oder mit einem einfachen Spannungsteiler aus der Betriebsspannung generieren. Bei der Berechung des Spannungsteilers zur Referenzspannungserzeugung kann man einen der Widerstände frei wählen. Alle Berechnungen können mit dieser einfachen Exceltabelle durchgeführt werden.

Invertierender Schmitt-Trigger

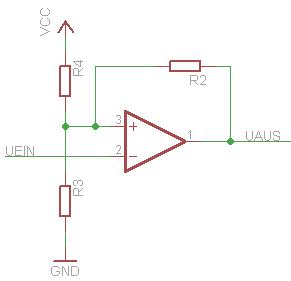
Invertierender Schmitt-Trigger

Durch einfaches Vertauschen von Uein und Uref kann die Schaltung invertierend arbeiten. Dabei ändern sich allerdings die Formeln zur Berechnung der Widerstände bzw. der Referenzspannung. Dafür gelten 2 Formeln.

[math]\displaystyle{ U_H=U_{ref} + (U_{HA}-U_{ref}) \frac{R_1}{R_1 + R_2} }[/math]

[math]\displaystyle{ U_L=U_{ref} - (U_{ref}-U_{LA}) \frac{R_1}{R_1 + R_2} }[/math]

Durch Umformen und Einsetzen erhält man:

[math]\displaystyle{ R_2=R_1 \frac{U_H-U_{HA}-U_L+U_{LA}}{U_L-U_H} }[/math]

Bei der Berechung des Spannungsteilers zur Erzeugung der Referenzspannung kann man keinen der Widerstände R3 und R4 frei wählen (welche zusammen R1 ersetzen), sie berechnen sich direkt aus R1 und den anderen Eingangsparametern, abgeleitet aus den beiden Formeln.

[math]\displaystyle{ R_{1}= R3//R4 = \frac{R_3 \cdot R_4}{R_3 + R_4} }[/math]

[math]\displaystyle{ U_{ref}= V_{CC} \frac{R_3}{R_3 + R_4} }[/math]

Durch Umformen und Einsetzen erhält man:

[math]\displaystyle{ R_{4}= R_1 \cdot \frac{V_{CC}}{U_{ref}} }[/math]

[math]\displaystyle{ R_{3}= R_4 \cdot \frac{U_{ref}}{V_{CC} - U_{ref}} }[/math]

Auch diese Berechungen sind in der Exceltabelle verfügbar.

Siehe auch

• Forumsbeitrag: OP als Schmitt Trigger
• Forumsbeitrag: Professioneller Grenzwertschalter (Hersteller)
• Forumsbeitrag: Fensterkomparator mit Hysterese und LEDs
• Forumsbeitrag: Fensterkomparator mit Hysterese und LEDs mit ATtiny13