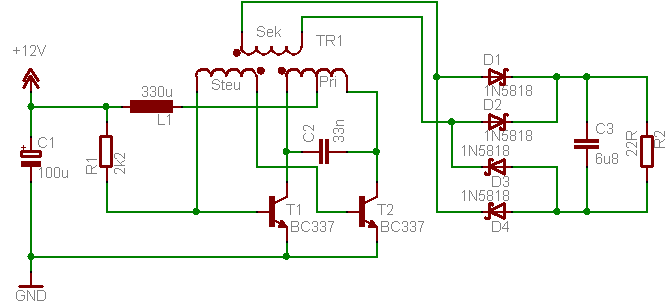
Royer Converter
Ein Royer-Converter ist ein Sinus-Leistungsoszillator. Er wird im Wesentlichen als Schaltnetzteil verwendet.
Geschichtliches
Der Name geht auf George Howard Royer zurück, welcher diese Schaltung im Jahr 1954 entwickelte (siehe US-Patent 2783384). Die originale Schaltung arbeitet mit einem Trafo mit Ferritkern, welcher zum Umschalten in die Sättigung getrieben wird. Das Ausgangssignal ist rechteckförmig. Die hier vorgestellte Version, die auf Peter James Baxandall zurückgeht (siehe IEE-Paper Transistor Sine-Wave LC Oscillators, 1959), arbeitet jedoch mit einem Trafo, welcher nicht in die Sättigung geht und mittels LC-Schwingkreis ein Sinussignal erzeugt. Der Trafo kann sogar als Luftspule ohne Kern ausgeführt werden.
Aufbau und Eigenschaften
Der Aufbau ist sehr einfach und robust. Zwei Transistoren (MOSFETs oder Bipolar) werden wechselseitig geschaltet (Gegentaktbetrieb, engl. push pull), und damit abwechselnd die eine und die andere Spulenhälfte der Primärwicklung von Strom durchflossen. Die Schaltung ist selbstschwingend, d.h. das Steuersignal wird direkt aus dem Trafo zurückgewonnen. Damit schwingt sie immer optimal auf Resonanz, ohne Abgleich von Bauteiltoleranzen und auch bei Alterung oder Temperaturänderung. Allerdings ändert sich damit die Frequenz des Schwingkreises und damit geringfügig die Effizienz. Die Frequenz wird durch die Induktivität der Primärwicklung und den Kondensator C2 bestimmt (Parallelschwingkreis). Die Drosselspule L1 sorgt dafür, dass die Betriebsspannung wechselspannungsmäßig von der Mittelanzapfung von TR1 entkoppelt wird, sie wirkt als Konstantstromquelle.
- Einfacher, robuster Aufbau
- Sinusförmige Strom- und Spannungsverläufe
- Transistoren schalten im Nulldurchgang der Spannung, dadurch geringe Schaltverluste und Störstrahlung
- Bei ausreichend großer Streuinduktivität zwischen Primär- und Sekundärwicklung ist die Schaltung kurzschlussfest.
- Vollkommen unempfindlich gegenüber Streuinduktivitäten des Trafos (im Gegensatz zu den meisten anderen Schaltnetzteiltopologien)
Besonders der letzte Punkt ist sehr interessant. Auf Grund des Aufbaus und der Funktion wird sämtliche Energie im Magnetfeld, welche nicht über die Sekundärspule ausgekoppelt wird, wieder in den Schwingkreis zurückgeführt. Damit geht nur sehr wenig Energie verloren, egal wie gut die Kopplung zwischen Sekundär- und Primärspule ist.
Der Trafo TR1 kann sehr verschieden aufgebaut sein. In einem Inverter für CCFLs ist es ein normaler Trafo mit Ferritkern. In anderen Anwendungen kann es aber auch ein kernloser Trafo sein, bei dem es zwischen Primärspule und Sekundärspule einen großen Abstand gibt (Kontaktlose Energieübertragung).
Ein praktisches Beispiel
Auf Grund der Unempfindlichkeit der Schaltung gegenüber Streuinduktivitäten ist diese Schaltung ideal für einen Trafo ohne Kern und mit grossem Abstand zwischen Primär- und Sekundärspule. Damit kann kontaktlos recht viel Energie übertragen werden. Anwendungen sind z. B. die Ladestation elektrischer Zahnbürsten oder ein Rotationstrafo für eine Propelleruhr. Für Letzteres soll dieses Beispiel hier dargestellt werden.
Die Schaltung benutzt einfach beschaffbare Bauteile. Der Trafo wird selber gewickelt, ist aber auch vollkommen unkritisch. Wie im Bild zu sehen, wurde absichtlich ein recht grosser Luftspalt zwischen Primär- und Sekundärspule gelassen, um die Leistungsfähigkeit der Schaltung zu demonstrieren. Die Primärwicklung ist bifilar gewickelt, d.h. man nimmt den Draht doppelt und wickelt damit gleichzeitig beide Spulenhälften, das geschlossene Ende trennt man danach auf und verschaltet phasenrichtig. Es entstehen zwei verschachtelte Wicklungen (engl. interleaved windings), dadurch verbessert sich die Kopplung. Der Trafo hat folgende Parameter.
| Wicklung | Windungszahl | Drahtdurch- messer [mm] |
Durchmesser [mm] |
Induktivität [µH] |
|---|---|---|---|---|
| Primär | 2x10 | 0,55 | 80 | 70 |
| Steuer | 1 | 0,2 | 80 | --- |
| Sekundär | 13 | 0,55 | 65 | 23 |
| Bauteil | Wert | Reichelt Bestellnummer |
|---|---|---|
| T1, T2 | BC337 | 337-25 |
| L1 | 330µH; 0,5A | 09P 330µ |
| C1 | 100µF, 25V | RAD 100/25 |
| C2 | 33nF, 100V | MKP-10-630 33N |
| C3 | 6,8µF, 50V | MKS-2 6,8µ |
| R1 | 2k2, 1/4W | METALL 2,21K |
| R2 | 22R, 5W | 5W AXIAL 22 |
| D1-4 | 1N5818 | 1N 5818 |
| TR1 | CuL, 0,5mm | CUL 100/0,50 |
Mit 12V Eingangsspannung beträgt die Spannung im Primärkreis ziemlich genau 38Vpeak. Der Leerlaufstrom der Schaltung beträgt 36mA. ABER! Der Leerlaufstrom im Schwingkreis beträgt 583mA(eff), die Scheinleistung 15,7VA! Hier wird klar, warum sowohl die Primärspule als auch C2 sehr verlustarm sein müssen. Die Resonanzfrequenz beträgt 104.7 kHz. Damit wurden folgende Messwerte erreicht.
| Belastung | Eingangs- strom [mA] |
Ausgangs- strom [mA] |
Ausgangs- spannung [Veff] |
Ausgangs- leistung [W] |
Wirkungs- grad [%] |
|---|---|---|---|---|---|
| Leerlauf | 36 | 0 | 7,8 | 0 | 0 |
| 22 Ω | 220 | 320 | 7 | 2,2 | 84 |
| Gleichrichter + 22 Ω | 190 | 270 | 6 | 1,6 | 71 |
| 10 Ω | 250 | 490 | 4,9 | 2,4 | 80 |
| Kurzschluß | 60 | 650 | 0 | 0 | 0 |
Nach Gleichrichtung mit schnellen Schottkydioden und Filterung bleiben bei 22Ω Last noch ca. 6V Gleichspannung übrig, genug um mit einem Low Drop Spannungsregler stabile 5V für einen Mikrocontroller bereitzustellen. Selbst bei der recht hohen Ausgangsleistung bleiben alle Bauteile kühl. Dabei werden nur recht kleine Transistoren verwendet. Das zeigt umso mehr die Leistungsfähigkeit der Schaltung. Bei optimaler Leistungsanpassung mit 10 Ω Last kann man 2,4W aus dem Trafo entnehmen. Diese Leistung wird vor allem durch den recht geringen Koppelfaktor von nur 0,45 begrenzt. Dieser kommt allerdings dem Kurzschlussfall zu gute, hier beträgt die Stromaufnahme der Schaltung nur 60mA, die Resonanzfrequenz steigt nur mässig auf 123kHz. Prinzipiell ist diese Schaltung bis in den Bereich von mehreren kW Leistung skalierbar.
Hinweise
- Beim ersten Einschalten unbedingt die Strombegrenzung am Netzteil einstellen! Für die Beispielschaltung reichen 100mA.
- Schwingt die Schaltung nicht an, ist in den meisten Fällen die Steuerwicklung verpolt.
- Manchmal ist auch die Primärwicklung falsch angeschlossen. Beim bifilaren Wickeln muss man das geschlossene Ende aufschneiden und das linke Ende der nun entstandenen Teilwicklung mit dem rechten Ende der zweiten Teilwicklung zur Mittelanzapfung verbinden.
- Der Kondensator C2 wird auch im Leerlauf von einem recht hohen Strom durchflossen. Deshalb muss hier auf jeden Fall ein verlustarmer Typ eingesetzt werden. Entweder ein Folienkondensator mit Polypropylen als Dielektrikum (MKP oder FKP) oder ein Keramikkondensator aus C0G oder NP0. Andere Typen (Folie MKS, Keramik X7R, Z5U etc.) gehen nicht, denn hier werden zu hohe dielektrische Veluste im Kondensator erzeugt, welche diesen erhitzen und irgendwann zerstören. Die Verluste von X7R sind ca. 20mal höher als von NP0!
- Die Transistoren sollten nur mässig überdimensioniert sein, denn Transistoren mit sehr hohen Kollektorströmen sind meist auch recht langsam.
- Die Transistoren müssen mindestens eine Sperrspannung von [math]\displaystyle{ \pi \cdot U_{ein} }[/math] aushalten, denn das ist die exakte Amplitude der Schwingung im Primärkreis. Praktisch sollte man aber mindestens 20% und mehr Reserve einplanen.
- Der Basiswiderstand muss experimentell ermittelt werden. Er muss so ausgelegt sein, dass die Transistoren beim Schalten nur schwach in die Sättigung gehen, um schneller wieder abschalten zu können (Stichwort Speicherzeit, engl. storage time).
- Die Drossel L1 sollte ca. den 2..3fachen Induktivitätswert der Primärwicklung haben. Je mehr, umso besser. Sie darf bei vollem Laststrom nicht in die Sättigung gehen, da dann ihre Induktivität stark absinkt.
- Man sollte keine Drahtpotis zur Lastvariation nutzen, wenn man das direkt an der Wechselspannung der Sekundärseite macht. Die haben soviel Induktivität (im Test 12µH, =8Ω bei 105kHz), dass die dadurch den Maximalstrom ungewollt verringern. Selbst einfache Drahtwiderstände sind mit 3µH/2Ω induktivem Anteil schon ungünstig. Verwendet man allerdings einen Gleichrichter, ist das unkritisch.
- Die Spitzenspannung der Steuerwicklung darf ca. 5V nicht überschreiten, weil diese als Sperrspannung für die Transistoren wirksam wird. Die meisten Bipolartransistoren verkraften max. 5V Sperrspannung zwischen Basis und Emitter.
- Im Kurzschlussfall der Sekundärwicklung reduziert sich die Induktivität der Primärwicklung auf die Streuinduktivität, was zu einer Frequenzerhöhung führt. Durch die höhere Frequenz stellt die Streuinduktivität einen höheren Blindwiderstand dar, welcher den Strom wirkungsvoll begrenzt. Aufgrund der höheren Frequenz fließt allerdings ein größerer Strom im Schwingkreis. Verwendet man also diesen Zustand, dann muss die Schaltung für die höheren Belastungen ausgelegt sein. Je kleiner der Koppelfaktor, umso besser die Kurzschlussfestigkeit. Die nachfolgende Tabelle gibt die Erhöhung des Eingangsstroms sowie der Resonanzfrequenz beim Kurzschluss in Abhängigkeit des Koppelfaktors an.
- Ein großer Vorteil des Royer Converters mit Bipolartransistoren und Hilfswicklung ist die Anschwingfreudigkeit. D.h. die Schaltung schwingt SEHR sicher an, auch bei kleinsten Spannungen und beim sehr langsamen Anstieg der Versorgungsspannung.
| Koppel- faktor |
Faktor gegenüber Leerlauf | |
|---|---|---|
| Resonanz- frequenz |
Eingangs- strom | |
| 0,01 | 1,0 | 1,0 |
| 0,1 | 1,1 | 1,1 |
| 0,2 | 1,1 | 1,3 |
| 0,5 | 1,4 | 2,0 |
| 0,6 | 1,6 | 2,5 |
| 0,7 | 1,8 | 3,3 |
| 0,8 | 2,2 | 5 |
| 0,9 | 3,2 | 10 |
| 0,95 | 4,5 | 20 |
| 0,99 | 10 | 100 |
Formeln zum Royer Converter
- [math]\displaystyle{ f_r=\frac{1}{2 \pi \sqrt{L_{pri} C_2}} }[/math]
- [math]\displaystyle{ U_p = \pi \cdot U_{ein} }[/math]
- [math]\displaystyle{ I_p = U_{ein} \cdot \pi \sqrt{\frac{C}{L}} }[/math]
- [math]\displaystyle{ k = \frac {U_{aus}}{\pi \cdot U_{ein}} \cdot \frac {N_{pri}}{N_{sek}} }[/math] (im Leerlauf gemessen)
- [math]\displaystyle{ k = \sqrt{1-\frac{L_{Pri-K}}{L_{Pri-0}}} }[/math] (mit L-Meter gemessen)
- [math]\displaystyle{ R1 \sim \frac{\beta _{I_N} \cdot U_{ein}}{I_N} }[/math]
- [math]\displaystyle{ N_{steu} \le \frac{5}{\pi \cdot U_{ein}}\cdot N_{Pri} }[/math]
- [math]\displaystyle{ P_{max}=\frac{(\pi \cdot U_{ein} \cdot k)^2 \sqrt{L_{pri} \cdot C_2 (1-k^2)}}{4 \cdot L_{pri} \cdot (1-k^2)} }[/math] (Näherungsformel)
- [math]\displaystyle{ R_{opt}=(1-k^2)(\frac{N_{sek}}{N_{pri}})^2 L_{pri} \cdot 2\pi \cdot f }[/math]
| Formelzeichen | Bedeutung |
|---|---|
| [math]\displaystyle{ \!\, f_r }[/math] | Resonanzfrequenz im Leerlauf |
| [math]\displaystyle{ \!\, L_{Pri} }[/math] | Induktivität der Primärwicklung |
| [math]\displaystyle{ \!\, C2 }[/math] | Kapazität des Primärschwingkreises |
| [math]\displaystyle{ \!\, U_p }[/math] | Spitzenspannung im Resonanzkreis |
| [math]\displaystyle{ \!\, I_p }[/math] | Spitzenstrom im Resonanzkreis |
| [math]\displaystyle{ \!\, k }[/math] | Koppelfaktor zwischen Primär- und Sekundärwicklung |
| [math]\displaystyle{ \!\, L_{Pri-0} }[/math] | Primärinduktivität bei Leerlauf der Sekundärwicklung |
| [math]\displaystyle{ \!\, L_{Pri-K} }[/math] | Primärinduktivität bei Kurzschluss der Sekundärwicklung |
| [math]\displaystyle{ \!\, U_{ein} }[/math] | Eingangsspannung des Royer Converters (Gleichspannung) |
| [math]\displaystyle{ \!\, U_{aus} }[/math] | Ausgangsspannung des Royer Converters (Wechselspannung, Spitzenwert) |
| [math]\displaystyle{ \!\, R1 }[/math] | Basiswiderstand |
| [math]\displaystyle{ \!\, I_N }[/math] | Nennstrom des Royer Converters am Eingang |
| [math]\displaystyle{ \!\, \beta _{I_N} }[/math] | Stromverstärkung der Transistoren bei Nennstrom Achung! Die Stromverstärkung sinkt bei höheren Strömen deutlich, ins Datenblatt schauen. |
| [math]\displaystyle{ \!\, N_{steu} }[/math] | Windungszahl der Steuerwicklung |
| [math]\displaystyle{ \!\, P_{max} }[/math] | Maximale Ausgangsleistung bei Leistungsanpassung |
| [math]\displaystyle{ \!\, R_{opt} }[/math] | Optimaler Lastwiderstand für Leistungsanpassung |
Das Ganze ist auch als Exceltabelle zur leichten Anwendung verfügbar.
Leistungsoptimierung
Wie kann ich den Wirkungsgrad sowie die Ausgangsleistung für meine Anwendung optimieren?
- Die Eingangsspannung soll möglichst hoch sein.
- Der Koppelfaktor soll möglichst hoch sein. Das erreicht man durch
- Flache Spulen mit grossem Durchmesser und kleinem Abstand (parallele Spulen)
- Konzentrische (ineinandergestapelte) Spulen mit geringem Luftspalt zwischen den Spulen
- Einsatz von Ferritkernen (Schalenkerne, Stäbe etc.) zur Bündelung des Magnetfeldes
- Wenn man die Sekundärwicklung mit einem parallel oder in Reihe geschalteten Kondensator auf Resonanz mit der Primärwicklung abgleicht, kann die Ausgangsleistung deutlich erhöht werden, weil dadurch die Streuinduktivität der Sekundärseite kompensiert wird. Man muss dabei beachten, dass bei Parallelschaltung die Ausgangsspannung ohne Last stark ansteigt (Prinzip der Teslaspule). Unter Last verhält sich der Ausgang dann nahezu wie eine Konstantstromquelle. Bei Reihenschaltung ist das nicht der Fall, hier bleibt die Leerlaufspannung niedrig. Auch für diesen zusätzlichen Kondensator gilt das Gleiche wie C2, er muss sehr verlustarm sein. Es gilt
- [math]\displaystyle{ C_{sek} = \frac{1}{(2 \pi f)^2 L_{sek}\sqrt{1-k^2}} }[/math]
- Das Verhältnis [math]\displaystyle{ C/L }[/math] soll möglichst hoch sein. Verdoppelt man die Kapazität und reduziert gleichzeitig die Primärinduktivität um den Faktor zwei (Windungszahl * 0,7), verdoppelt sich die maximal verfügbare Leistung. Der Preis dafür sind doppelt so hohe Leerlaufströme im Schwingkreis und damit ca. 2,8mal so hohe Leerlaufverluste (bei gleichem Drahtquerschnitt, P = I^2 * R).
- Die Resonanzfrequenz soll möglichst niedrig sein, daduch veringern sich die induktiven Widerstände der Streuinduktivitäten, welche den Strom und damit die Leistung begrenzen.
- Der Drahtquerschnitt der Primärwicklung muss möglichst gross sein, denn hier fließen sehr hohe Ströme. Allerdings bewirkt die meist recht hohe Resonanzfrequenz auf grund des Skineffekts eine Verringerung des effektiven Drahtquerschnitts. Ausserdem lassen sich dicke, massive Kupferdrähte eher schlecht wickeln. Darum verwendet man oft HF-Litze, welche aus sehr vielen, sehr dünnen, gegeneinander isolierten Drähten besteht. Diese lässt sich deutlich besser wickeln und wirkt dem Skineffekt entgegen.
- Bei einem 1:1 Transformator kann die Sekundärseite gleich aufgebaut werden wie die Primärseite (zwei kreuzgekoppelte Schalttransistoren). Die Transistoren arbeiten dann als Synchrongleichrichter und der Spannungsabfall der Gleichrichterdioden fällt weg (steigert den Wirkungsgrad). Achtung! Durch den symmetrischen Aufbau kann Energie in beide Richtungen übertragen werden.
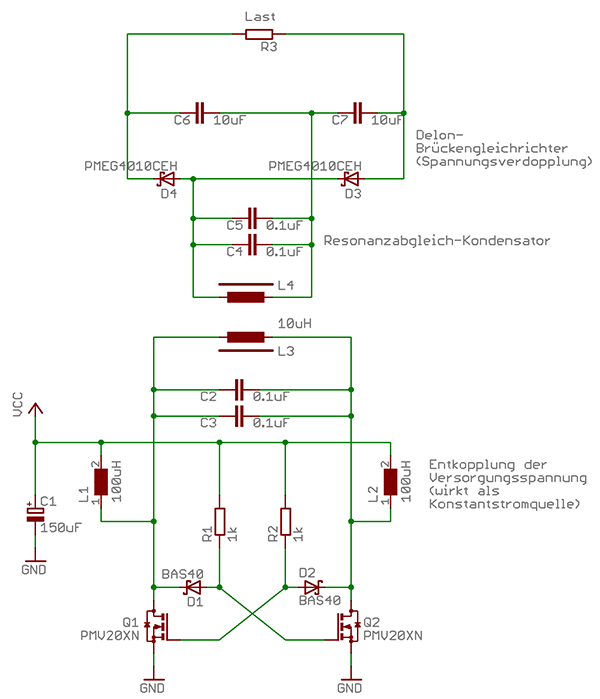
MOSFET-Variante
Man kann die Primärseite des Trafos mit Mittelanzapfung und Steuerwicklung auch durch eine einfache Spule ersetzen, wenn man MOSFETs statt Bipolartransistoren nutzt und die Betriebsspannung über zwei Spulen an den Enden der Primärwicklung einspeist. Das vereinfacht den Aufbau der Primärspule deutlich, was u.a. bei höheren Leistungen günstig ist. Der Preis dafür ist, daß man zwei Spulen mit etwa der doppelten Induktivität benötigt. Ebenfalls werden dazu geeignete Flachspulen von Herstellern wie Würth Elektronik eiSos, TDK, etc. produziert, Stichwort: Ladespule bzw. charging coil. Im Bild links unten die kleinste Ladespule mit 10µH, mittig oben 6.3µH, rechts unten 6.3µH mit einem Neodym-Magnet in der Mitte.
Die unten abgebildete Mosfet-Schaltung baut auf einem Beitrag aus dem Forum auf, in dem auch weitere Erklärungen der Funktionsweise sowie zahlreiche Dimensionierungsbeispiele enthalten sind. Eine dazugehörige Simulation in LTSpice kann hier gefunden werden. Die Effizienz scheint in der Simulation niedriger als in der Realität zu liegen, jedoch eignet sich die Simulation ideal zum Verstehen sowie dem schnellem Testen der Auswirkungen unterschiedlicher Bauteilvarianten wie bspw. der Ermittlung der optimalen Eingangsinduktivität oder Gate-Widerstände.
Im Bild sieht man links die Royer-Converter Schaltung, an welche die kleine Ladespule von Würth Elektronik eiSos mit 10µH angeschlossen ist. Darüber die selbst gewickelte Empfangsspule sowie der Ferritkern welcher im Betrieb hinter die Empfangsspule befestigt wird. Die Empfangsspule ist mit dem Gleichrichter verbunden welcher den DC-DC Buck-Converter speist. Der Lastwiderstand ist rechts außen sichtbar. Im Betrieb sind beide Spulen parallel übereinander im Abstand von 3mm ausgerichtet, getrennt durch eine Acrylplatte.
Beispieleinsatz:
Die in obiger Schaltung verwendeten Bauteile sind für eine drahtlose Energieübertragung mit einer Eingangsspannung von 5V, einer Ausgangsspannung von 5V und Ausgangsleistung von 2.2W bei einem Abstand von 3mm ausgelegt. Als Primärspule wird eine 10µH Ladespule von Würth Elektronik eiSos verwendet, als Sekundärspule eine selbstgewickelte Flachspule mit 14mm Durchmesser und 14 Windungen auf deren Rückseite ein Pot Core Ferritkern (3H1) zur Leistungsverbesserung plaziert ist. Die hier verwendeten Mosfets sind Logic-Level-Mosfets und nicht für hohe Eingangsspannungen ausgelegt (im oben genannten Beitrag finden sich Beispiele für Eingangsspannungen >10V). Um die Ausgangsspannung auf 5V zu stabilisieren, wird der Buck-Converter TPS54331 verwendet (nicht in der Schaltung aufgeführt), der eine Ein-/Ausschalthysterese besitzt um nur bei geeigneter Orientierung der Spulen einzuschalten und dadurch stabile 5V erzeugen kann. Die komplette Schaltung ist mit SMD Bauteilen und 0.1µF NP0 50V Kondensatoren in der Bauform 1206 aufgebaut worden (siehe rechte Abbildung). Bei den Spulen L1 und L2 muss ein Mittelmaß zwischen Baugröße, Induktivität und Widerstand gefunden werden. Bei gleichbleibender Baugröße stellte 100µH die optimale Wahl im Vergleich zu 47µH (zu geringe Induktivität) und 220µH (zu hoher Widerstand) dar. Die so aufgebaute Schaltung arbeitet bei 115kHz und erreicht momentan einen Wirkungsgrad von ca. 58% bei einer Ausgangsleistung von 5V*450mA.
Wie im Artikel beschrieben, kann die Effizienz gesteigert werden, indem die Fläche der Sekundärspule vergrößert wird, Lastanpassung vorgenommen wird, optimierte Ferritkerne verwendet werden etc. Bei identischer Primär- und Sekundärspule (WE-WPCC 10µH von Würth Elektronik eiSos) im Abstand von 5mm und einem Lastwiderstand von 68 Ω direkt am Delon-Brückengleichrichter angeschlossen (ohne DC-DC Converter) wurde in einem kurzen Versuch eine Effizienz von ca. 70% gemessen, bei einer Ausgangsleistung von ca. 4W (19V @ 220mA) mit sonst unveränderten Parametern (5V @ 1.2A Eingang). Da an der Schaltung nichts verändert wurde und auch der Lastwiderstand eher zufällig gewählt wurde ist es offensichtlich, dass der maximale Wirkungsgrad noch nicht erreicht ist und somit weiteres Potenzial im Aufbau steckt.
Ein schneller Lochraster-Laboraufbau eines "Doppel Royer Converters" (gleicher Aufbau für die Sekundärseite wie für die Primärseite => Synchrongleichrichtung) erreichte einen Wirkungsgrad von 92% bei einer übertragenen Leistung von 300W (R_Last = 2,1Ohm). Als Übertrager wurde ein PM87/70 N87 Ferritkern mit 6 Windungen 0,1mm*240 Hochfrequenzlitze verwendet. Der Abstand der beiden Ferritkerne betrug dabei 4mm (=> Luftspalt von 8mm). Die Resonanzkapazität von 1,2µF wurde auf Primär- und Sekundärseite gleichmäßig aufgeteilt. Mit optimierten Aufbau erscheint ein Wirkungsgrad von ~95% möglich zu sein.
Hinweise zur MOSFET-Variante
- Die MOSFET-Variante des Royer Converters ist sehr empfindlich beim Einschalten. Steigt die Versorgungsspannung zu langsam an, leiten beide MOSFETs gleichzeitig und die Schaltung schwingt nicht an, was zu starker Erwärmung oder sogar zum Durchbrennen führen kann, wenn die Stromversorgung keine ausreichend kleine Strombegrenzung hat. Abhilfe schafft hier ein Sperren der Gates, bis die Versorgungsspannung ausreichend hoch ist. Danach werden die Gates schlagartig freigegeben und die Schaltung schwingt sicher an. Dafür braucht es nur 2 Dioden und einen Schalter, wie es in diesem Forumsbeitrag zu sehen ist. Der Schalter kann auch durch ein Transistor ersetzt werden, um den Royer-Converter per Digitalsignal bzw. Mikrocontroller zu steuern.
Siehe auch
Diskussionen im Forum
- Verwendung in einem Induktionsofen, MOSFETs als Schalter
- Verwendung in einem Induktionsofen, neuer Thread
- Dokumente über Induktionskochfelder
- Dokument über drahtlose Energieübertragung
- Komplettes Projekt einer Propelleruhr und lange Diskussion
- Noch eine Propelleruhr
- Royer Converter mit Schalenkernen und 20W Ausgangsleistung
- Royer Converter mit Luftspulen und 14W Ausgangsleistung
- Kleiner Royer Converter für einen Propellerglobus
- Herleitung der Formeln im Artikel Royer Converter
- berührungslos Bleigel Akku laden, 12V/1,6W
- Kleiner Wandler für 5V/250mW
- Automatische Lasterkennung und Steuerung für den Royer Converter
- RFID Spulen für Leistungsübertragung?
- Flachspule 1 mH -- wie selbst herstellen?
- Leistungsverbesserung Royer Converter
- WiTricity heute
- Ferritplatten
- Funktionsprinzip Royer Converter MOSFET
- Gekoppelte Schwingkreise / Drahtlose Energieübertragung
- Royer Converter - Spannungsspitzen
- Wechselspannung 117 kHz 80 vpp erzeugen
- Simulation der MOSFET-Variante
Weblinks
- Kleiner Wandler: Sehr ausführliche Beschreibung des Aufbaus und Berechnung der Komponenten
- Ernsthafter Wandler: Das Ganze nochmal in Groß
- Parallel-Resonant Push-Pull Converter Jonathan David Paolucci - Master Thesis
- Dokument zur kontaktlosen Energieübertragung
- AN14: Application Note von Zetex, englisch
- DN164: Design Note von Linear Technology, englisch
- Linear Technology Application Note 118: High Voltage, Low Noise, DC/DC Converters
- Schönes Projekt zur kontaktlosen Energieübertragung <---- Achtung: Seite hat einen Virus!!!
- Video zum Projekt
- Royer-Hochleistungsoszillatoren mit MOSFETs und IGBTs
- Diverse Schaltungsbeispiele
- Royer Oszillator für CCFL-Lampen
- Induktivität einer Kreisringspule
- The Baxandall parallel-resonant Class-D oscillator
- bq51013, IC zur kontaklosen Energieübertragung von TI, Evaluationboard verfügbar
- Wireless Power Consortium, definiert einen Standard zur kontaktlosen Energieübertragung (Qi)
- Welding inverter for 5$, Youtube Video mit Schaltplan
- Kontaktlose Energieübertragungslösungen von Firmen
- Schleifring, 100W - 200kW
- IST Sensorik GmbH, Milliwatt bis 1kW
- J-Lasselop, Mikrowatt bis 500kW
- EnASYS, 60W-500kW
- KONTENDA, 1W-2kW
- MESA Systemtechnik, Power- und Sensortelemetrie
- Wirelesspower, Anbieter von verschiedenen ICs und Modulen von 1W-3kW
- RRC Power Solutions - Plattform Kabellose Energie- / Datenübertragung, 5W, Qi kompatibel
- WE Online Wireless Power Transfer für hohe Leistungen im industriellen Umfeld
- Primove, kontakloses Laden für Busse, Autos und Straßenbahnen